algorithms-part4-6
algorithms-part4-6
algorithms-part4-6
Chapter 4
Paths in graphs
4.1 Distances
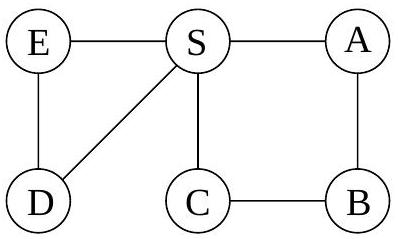
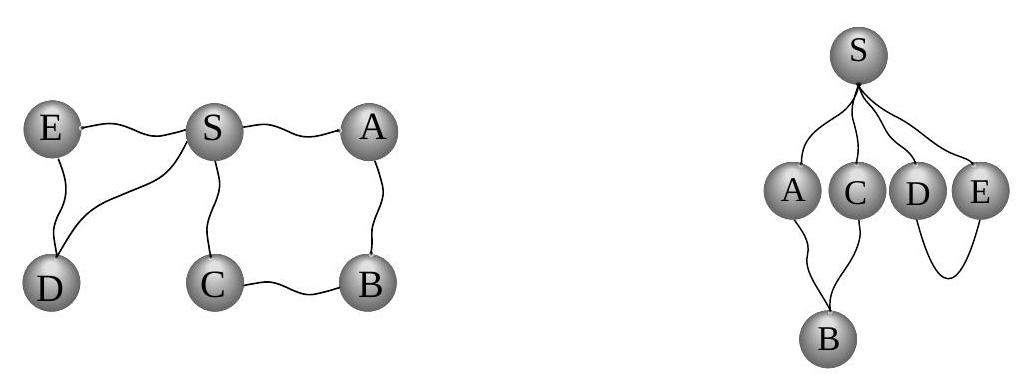
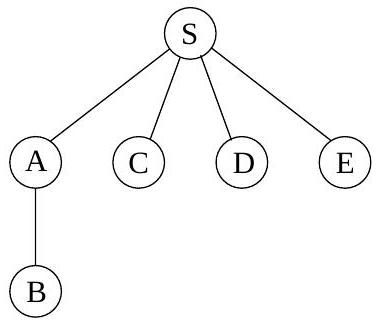
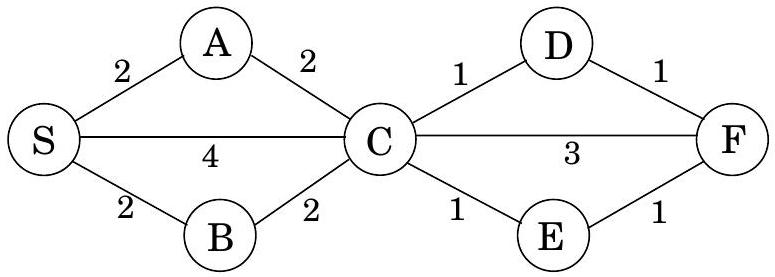
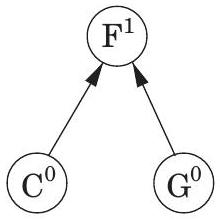
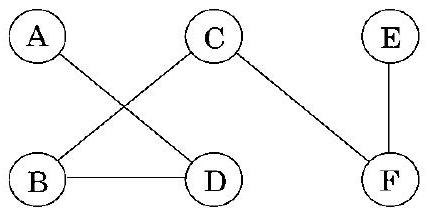
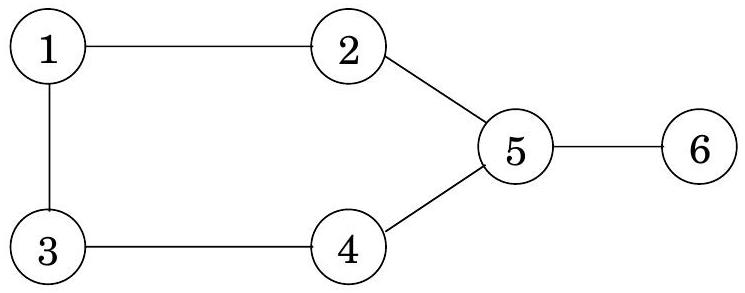
**깊이 우선 탐색(Depth-first search)**은 지정된 시작점으로부터 도달할 수 있는 그래프의 모든 정점을 쉽게 식별한다. 또한, **탐색 트리(search tree)**에 요약된 이 정점들에 대한 명시적인 경로를 찾는다(그림 4.1). 그러나 이러한 경로가 가능한 가장 경제적인 경로가 아닐 수도 있다. 그림에서 정점 는 단 하나의 edge를 통과하여 로부터 도달할 수 있지만, DFS 트리는 길이가 3인 경로를 보여준다. 이 장은 그래프에서 **최단 경로(shortest paths)**를 찾는 알고리즘에 관한 것이다.
경로 길이를 통해 그래프의 서로 다른 정점들이 얼마나 분리되어 있는지 정량적으로 이야기할 수 있다:
두 노드 사이의 **거리(distance)**는 그들 사이의 최단 경로의 길이이다. 이 개념을 구체적으로 이해하기 위해, 각 정점에 공이 있고 각 edge에 끈이 있는 그래프의 물리적 구현을 생각해 보자. 정점 에 해당하는 공을 충분히 높이 들어 올리면, 함께 끌려 올라오는 다른 공들은 정확히 로부터 도달 가능한 정점들이다. 그리고 로부터의 거리를 찾으려면, 아래에 얼마나 매달려 있는지 측정하기만 하면 된다.
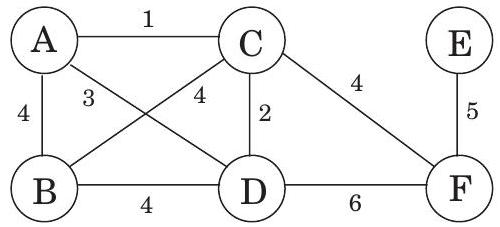
예를 들어, 그림 4.2에서 정점 는 로부터 거리가 2이며, 그곳으로 가는 두 개의 최단 경로가 있다. 가 위로 들려 있을 때, 이 각 경로를 따라 있는 끈들은 팽팽해진다.
그림 4.1 (a) 간단한 그래프와 (b) 그 깊이 우선 탐색 트리.
(a)
(b)
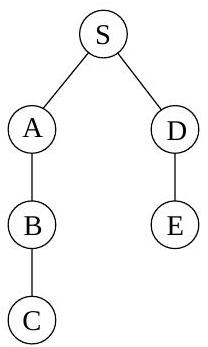
그림 4.2 그래프의 물리적 모델.
반면에 edge ()는 어떤 최단 경로에서도 역할을 하지 않으므로 느슨한 상태로 남아 있다.
4.2 Breadth-first search
그림 4.2에서 의 리프팅은 그래프를 자체, 로부터 거리가 1인 노드들, 로부터 거리가 2인 노드들 등으로 계층으로 나눈다. 로부터 다른 정점까지의 거리를 계산하는 편리한 방법은 계층별로 진행하는 것이다. 거리가 인 노드들을 선택하고 나면, 거리가 인 노드들은 쉽게 결정된다. 이들은 거리가 인 계층에 인접하면서 아직 방문하지 않은 노드들이다. 이는 어떤 주어진 시간에 두 계층이 활성화되는 반복적인 알고리즘을 제안한다: 완전히 식별된 계층 와, 계층 의 이웃을 스캔하여 발견되고 있는 계층 .
**너비 우선 탐색(BFS)**은 이러한 간단한 추론을 직접 구현한다(그림 4.3). 초기에는 큐 가 거리가 0인 단일 노드 로만 구성된다. 그리고 각 후속 거리 에 대해, 가 거리가 인 모든 노드를 포함하고 다른 것은 아무것도 포함하지 않는 시점이 있다. 이 노드들이 처리될 때(큐의 앞에서 제거될 때), 아직 방문하지 않은 이웃 노드들은 큐의 끝에 삽입된다.
이 알고리즘이 올바르게 작동하는지 확인하기 위해 이전 예시(그림 4.1)에 적용해 보자. 가 시작점이고 노드들이 알파벳 순서로 정렬되어 있다면, 그림 4.4에 표시된 순서대로 방문된다. 오른쪽에 있는 너비 우선 탐색 트리는 각 노드가 처음 발견되는 경로를 포함한다. 이전에 보았던 DFS 트리와 달리, 이 트리는 로부터의 모든 경로가 가능한 가장 짧은 경로라는 속성을 갖는다. 따라서 이는 최단 경로 트리이다.
Correctness and efficiency
우리는 너비 우선 탐색(breadth-first search)의 기본적인 직관을 개발했다. 알고리즘이 올바르게 작동하는지 확인하려면 이 직관을 충실히 실행하는지 확인해야 한다. 우리가 정확히 기대하는 바는 다음과 같다:
각 에 대해, (1) 로부터의 거리가 인 모든 노드의 거리가 올바르게 설정되고; (2) 다른 모든 노드의 거리는 로 설정되며; (3) 큐에는 거리가 인 노드만 정확히 포함되는 순간이 있다.
그림 4.3 너비 우선 탐색.
procedure bfs \((G, s)\)
Input: Graph \(G=(V, E)\), directed or undirected; vertex \(s \in V\)
Output: For all vertices \(u\) reachable from \(s\), dist(u) is set
to the distance from \(s\) to \(u\).
for all \(u \in V\) :
\(\operatorname{dist}(u)=\infty\)
dist \((s)=0\)
\(Q=[s]\) (queue containing just s)
while \(Q\) is not empty:
\(u=\operatorname{eject}(Q)\)
for all edges \((u, v) \in E\) :
if dist \((v)=\infty\) :
inject ( \(Q, v\) )
dist \((v)=\) dist \((u)+1\)
그림 4.4 그림 4.1의 그래프에 대한 너비 우선 탐색 결과.
| 방문 순서 | 노드 처리 후 큐 내용 |
|---|---|
| [] |
이는 귀납적 논증을 염두에 두고 표현되었다. 우리는 이미 **기저 사례(base case)**와 **귀납 단계(inductive step)**를 모두 논의했다. 세부 사항을 채울 수 있는가?
이 알고리즘의 전체 실행 시간은 깊이 우선 탐색(depth-first search)과 정확히 동일한 이유로 **선형 시간인 **이다. 각 정점은 처음 발견될 때 정확히 한 번 큐에 삽입되므로, 큐 작업은 번 발생한다. 나머지 작업은 알고리즘의 가장 안쪽 루프에서 수행된다. 실행 과정에서 이 루프는 각 엣지를 한 번(방향 그래프) 또는 두 번(무방향 그래프) 살펴보므로 시간이 소요된다.
이제 BFS와 DFS를 모두 살펴보았으니, 이들의 탐색 방식은 어떻게 비교될까? 깊이 우선 탐색은 그래프를 깊이 파고들며, 방문할 새로운 노드가 없을 때만 후퇴한다. 이 전략은 3장에서 보았듯이 훌륭하고 미묘하며 매우 유용한 속성을 제공한다. 그러나 이는 DFS가 실제로는 매우 가까운 정점까지 길고 복잡한 경로를 택할 수 있음을 의미하기도 한다(그림 4.1 참조). 너비 우선 탐색은 시작점으로부터의 거리가 증가하는 순서로 정점을 방문하도록 보장한다. 이는 물결의 전파와 같이 더 넓고 얕은 탐색이다. 그리고 DFS와 거의 동일한 코드—단, 스택 대신 큐를 사용한다—로 구현된다.
또한 DFS와의 한 가지 스타일적 차이점에 주목하라: 우리는 로부터의 거리에만 관심이 있으므로, 다른 연결 요소(connected components)에서는 탐색을 다시 시작하지 않는다. 로부터 도달할 수 없는 노드는 단순히 무시된다.
4.3 Lengths on edges
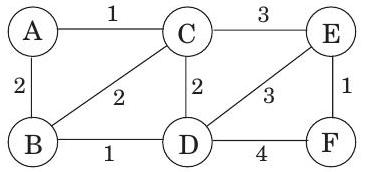
**너비 우선 탐색(Breadth-first search)**은 모든 edge의 길이가 같다고 가정한다. 하지만 최단 경로를 찾아야 하는 애플리케이션에서는 이러한 가정이 거의 맞지 않는다. 예를 들어, 샌프란시스코에서 라스베이거스로 운전하여 가장 빠른 경로를 찾고 싶다고 가정해 보자. 그림 4.5는 사용할 수 있는 주요 고속도로를 보여준다. 이들 중 올바른 조합을 선택하는 것은 각 edge(각 고속도로 구간)의 길이가 중요한 최단 경로 문제이다. 이 장의 나머지 부분에서는 이보다 더 일반적인 시나리오를 다룰 것이며, 모든 edge 에 길이 를 주석으로 달 것이다. 만약 라면, 때로는 또는 라고도 쓸 것이다.
그림 4.5 Edge의 길이는 종종 중요하다.
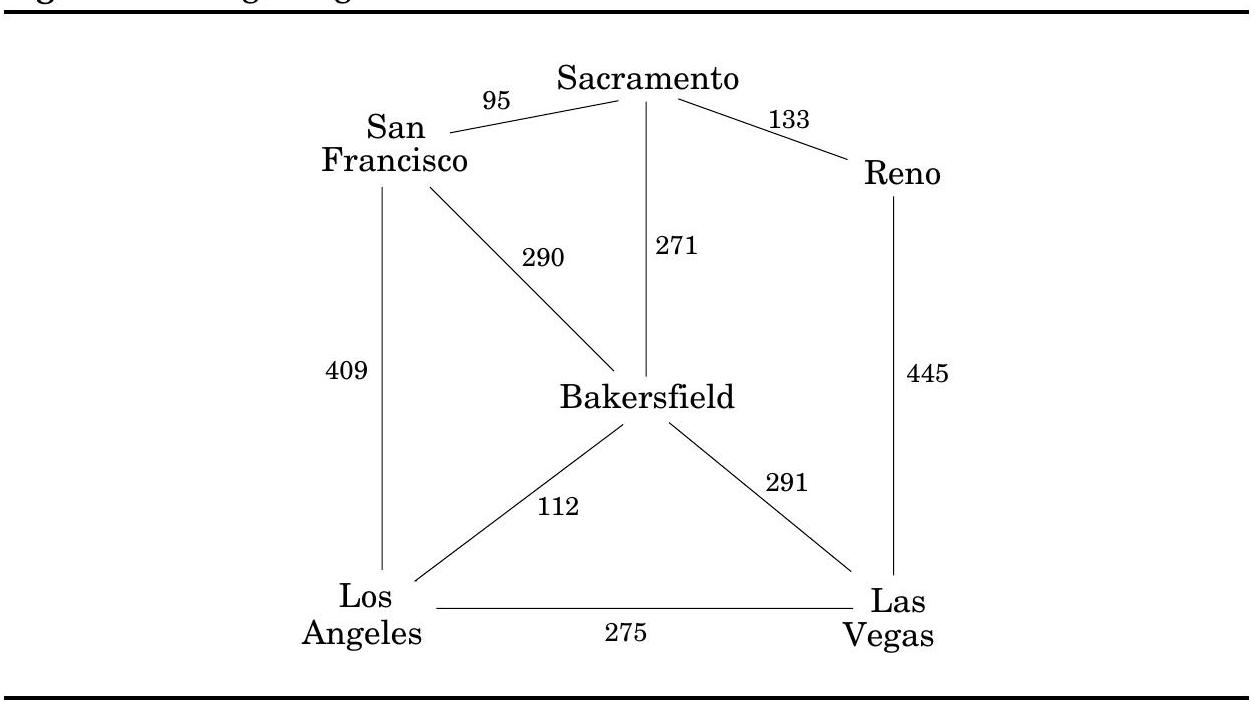
이 값은 물리적인 길이에 해당할 필요는 없다. 이는 시간(도시 간 운전 시간)이나 돈(버스 요금) 또는 우리가 절약하고 싶은 다른 어떤 양을 나타낼 수 있다. 사실, 음수 길이를 사용해야 하는 경우도 있지만, 이 특정 복잡성은 잠시 간과할 것이다.
4.4 Dijkstra's algorithm
4.4.1 An adaptation of breadth-first search
너비 우선 탐색(Breadth-first search)은 간선 길이가 단위인 모든 그래프에서 최단 경로를 찾는다. 이를 간선 길이 가 양의 정수인 더 일반적인 그래프 에 적용할 수 있을까?
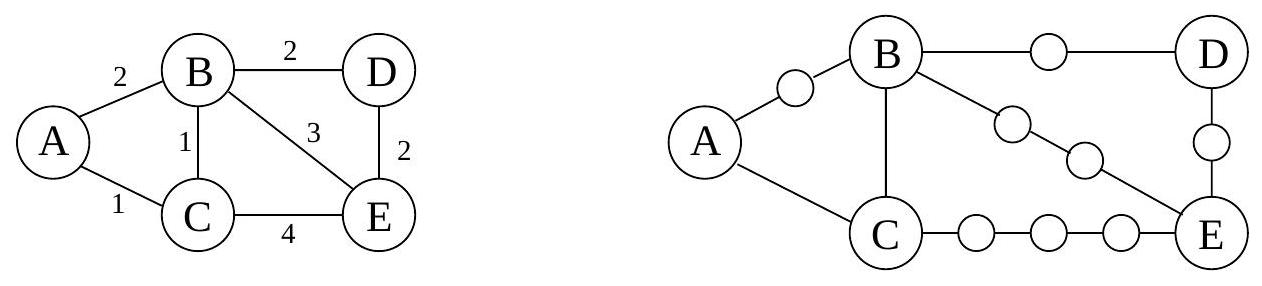
A more convenient graph
다음은 를 BFS가 처리할 수 있는 형태로 변환하는 간단한 방법이다: 의 긴 edge들을 "dummy" 노드를 도입하여 단위 길이 조각으로 나눈다. 그림 4.6은 이 변환의 예시를 보여준다. 새로운 그래프 를 구성하기 위해,
의 모든 edge 에 대해, 와 사이에 개의 dummy 노드를 추가하여 개의 길이 1인 edge로 대체한다.
그래프 는 우리가 관심 있는 모든 정점 를 포함하며, 이들 사이의 거리는 에서와 정확히 동일하다. 가장 중요한 것은 의 edge들이 모두 단위 길이라는 점이다. 따라서 에서 BFS를 실행하여 의 거리를 계산할 수 있다.
그림 4.6 Edge를 단위 길이 조각으로 나누기.
Alarm clocks
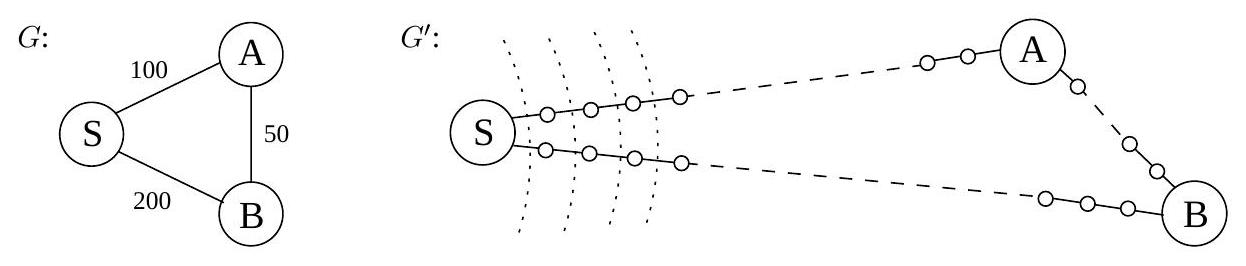
효율성이 문제가 되지 않는다면 여기서 멈출 수 있다. 그러나 가 매우 긴 edge를 가질 때, 는 더미 노드로 빽빽하게 채워지고, BFS는 우리가 전혀 신경 쓰지 않는 이 노드들까지의 거리를 부지런히 계산하는 데 대부분의 시간을 보낸다.
이를 더 구체적으로 이해하기 위해 그림 4.7의 그래프 와 를 고려하고, 의 노드 에서 시작된 BFS가 1분당 1단위 거리씩 진행한다고 상상해 보자. 처음 99분 동안 BFS는 끝없는 더미 노드의 사막인 와 를 따라 지루하게 진행한다. 이 지루한 단계를 건너뛰고 흥미로운 일이 발생할 때마다, 특히 원래 그래프 의 실제 노드 중 하나에 도달할 때마다 알람이 울리도록 할 수 있는 방법이 있을까?
우리는 처음에 두 개의 알람을 설정하여 이를 수행한다. 하나는 노드 에 대해 시간 에 울리도록 설정하고, 다른 하나는 에 대해 시간 에 울리도록 설정한다. 이들은 현재 travers하고 있는 edge를 기반으로 한 예상 도착 시간이다. 우리는 잠시 잠들었다가 에 깨어나 가 발견되었음을 확인한다. 이 시점에서 에 대한 예상 도착 시간은 으로 조정되고, 우리는 그에 따라 알람을 변경한다.
Figure 4.7 에서의 BFS는 대부분 특별한 사건이 없다. 점선은 초기 "wavefront"를 보여준다.
더 일반적으로, 주어진 순간에 BFS는 의 특정 edge를 따라 진행하고 있으며, BFS가 이동하는 모든 endpoint 노드에 대해 해당 노드에 대한 예상 도착 시간에 울리도록 설정된 알람이 있다. 이 중 일부는 BFS가 나중에 다른 곳에 도착하여 지름길을 찾을 수 있으므로 과대평가일 수 있다. 앞선 예시에서는 에 도착하자마자 로 가는 더 빠른 경로가 드러났다. 그러나 알람이 울리기 전에는 흥미로운 일이 발생할 수 없다. 따라서 다음 알람이 울리는 것은 BFS에 의해 wavefront가 실제 노드 에 도착했음을 알려야 한다. 그 시점에서 BFS는 에서 나가는 새로운 edge를 따라 진행하기 시작할 수 있으며, 해당 endpoint에 대해 알람을 설정해야 한다.
다음 "알람 시계 알고리즘"은 에서 BFS의 실행을 충실히 시뮬레이션한다.
- 노드 에 대해 시간 0에 알람 시계를 설정한다.
- 더 이상 알람이 없을 때까지 반복한다:
다음 알람이 노드 에 대해 시간 에 울린다고 가정하자. 그러면:
- 에서 까지의 거리는 이다.
- 에서 의 각 이웃 에 대해:
- 에 대한 알람이 아직 없으면, 시간 에 알람을 설정한다.
- 의 알람이 보다 늦게 설정되어 있다면, 이 더 이른 시간으로 재설정한다.
Dijkstra's algorithm
알람 시계 알고리즘은 양의 정수 간선 길이를 가진 모든 그래프에서 거리를 계산한다. 알람 시스템을 구현해야 한다는 점을 제외하면 거의 사용할 준비가 되어 있다. 이 작업에 적합한 데이터 구조는 우선순위 큐(priority queue)(일반적으로 힙을 통해 구현됨)이며, 이는 연결된 숫자 키 값(알람 시간)을 가진 요소(노드) 집합을 유지하고 다음 작업을 지원한다:
- Insert: 집합에 새 요소를 추가한다.
- Decrease-key: 특정 요소의 키 값 감소를 수용한다.
- Delete-min: 가장 작은 키를 가진 요소를 반환하고 집합에서 제거한다.
- Make-queue: 주어진 키 값을 가진 주어진 요소들로 우선순위 큐를 구축한다. (많은 구현에서 이는 요소를 하나씩 삽입하는 것보다 훨씬 빠르다.)
처음 두 작업은 알람을 설정할 수 있게 하고, 세 번째 작업은 다음에 울릴 알람이 무엇인지 알려준다. 이 모든 것을 종합하면 Dijkstra의 알고리즘(그림 4.8)을 얻을 수 있다.
그림 4.8 Dijkstra의 최단 경로 알고리즘.
procedure dijkstra( \(G, l, s\) )
Input: Graph \(G=(V, E)\), directed or undirected;
positive edge lengths \(\left\{l_{e}: e \in E\right\}\); vertex \(s \in V\)
Output: For all vertices \(u\) reachable from \(s\), dist ( \(u\) ) is set
to the distance from \(s\) to \(u\).
for all \(u \in V\) :
dist \((u)=\infty\)
\(\operatorname{prev}(u)=\) nil
dist \((s)=0\)
\(H=\) makequeue \((V)\) (using dist-values as keys)
while \(H\) is not empty:
\(u=\) deletemin \((H)\)
for all edges \((u, v) \in E\) :
if dist( \(v\) ) > dist( \(u\) ) + l( \(u, v\) ):
dist \((v)=\) dist \((u)+l(u, v)\)
\(\operatorname{prev}(v)=u\)
decreasekey( \(H, v\) )
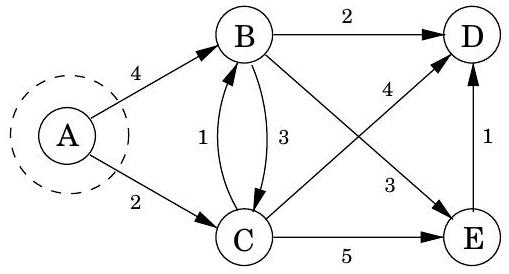
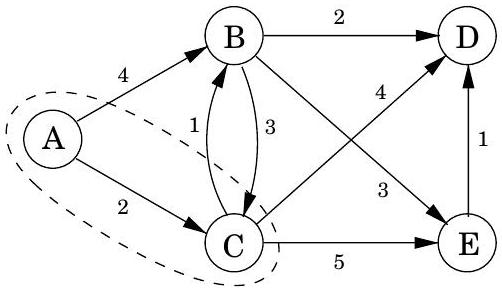
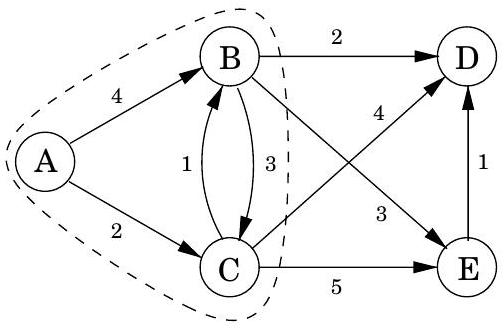
코드에서 dist 는 노드 에 대한 현재 알람 시계 설정을 나타낸다. 값은 알람이 아직 설정되지 않았음을 의미한다. 또한 각 노드 에 대한 중요한 정보인 prev라는 특수 배열이 있다: 에서 까지의 최단 경로에서 바로 앞에 있는 노드의 ID이다. 이 backpointer를 따라가면 최단 경로를 쉽게 재구성할 수 있으므로, 이 배열은 발견된 모든 경로의 간결한 요약이다. 알고리즘 작동의 전체 예시와 최종 최단 경로 트리는 그림 4.9에 나와 있다.
요약하자면, Dijkstra의 알고리즘은 BFS와 같다고 생각할 수 있지만, 간선 길이를 고려하여 노드의 우선순위를 정하기 위해 일반 큐 대신 우선순위 큐를 사용한다는 점이 다르다. 이러한 관점은 알고리즘이 어떻게 작동하고 왜 작동하는지에 대한 구체적인 이해를 제공하지만, BFS에 전혀 의존하지 않는 더 직접적이고 추상적인 유도가 있다. 이제 이 보완적인 해석으로 처음부터 시작한다.
그림 4.9 Dijkstra의 알고리즘 전체 실행 예시 (시작점: 노드 A). 관련 dist 값과 최종 최단 경로 트리도 함께 표시된다.
| A: 0 | D: |
|---|---|
| B: 4 | E: |
| C: 2 |
| A: 0 | D: 6 |
|---|---|
| B: 3 | E: 7 |
| C: 2 |
| A: 0 | D: 5 |
|---|---|
| B: 3 | E: 6 |
| C: 2 |
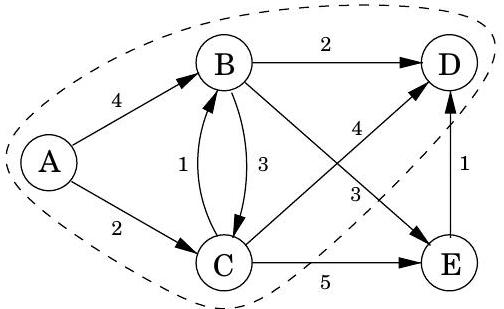
| A: 0 | D: 5 |
|---|---|
| B: 3 | E: 6 |
| C: 2 |
4.4.2 An alternative derivation
최단 경로를 계산하기 위한 계획은 다음과 같다: 시작점 에서 바깥쪽으로 확장하여, 거리가 알려진 그래프 영역과 최단 경로를 꾸준히 늘려나간다. 이 확장은 질서정연하게 이루어져야 하며, 가장 가까운 노드부터 먼저 포함하고 그 다음으로 더 멀리 있는 노드로 이동해야 한다. 더 정확히 말하면, "알려진 영역"이 를 포함하는 정점의 부분집합 일 때, 다음에 추가될 노드는 밖에 있으면서 에 가장 가까운 노드여야 한다. 이 노드를 라고 부르자. 질문은: 어떻게 를 식별하는가? 답을 찾기 위해, 에서 로 가는 최단 경로에서 바로 앞에 있는 노드 를 고려해보자:
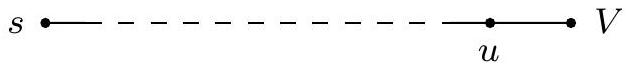
모든 edge 길이가 양수라고 가정했으므로, 는 보다 에 더 가깝다. 이는 가 안에 있다는 것을 의미한다. 그렇지 않다면 밖에 있는 에 가장 가까운 노드로서의 의 지위와 모순될 것이다. 따라서 에서 로 가는 최단 경로는 단순히 알려진 최단 경로가 단일 edge로 확장된 것이다.
Figure 4.10 알려진 최단 경로의 단일 edge 확장.
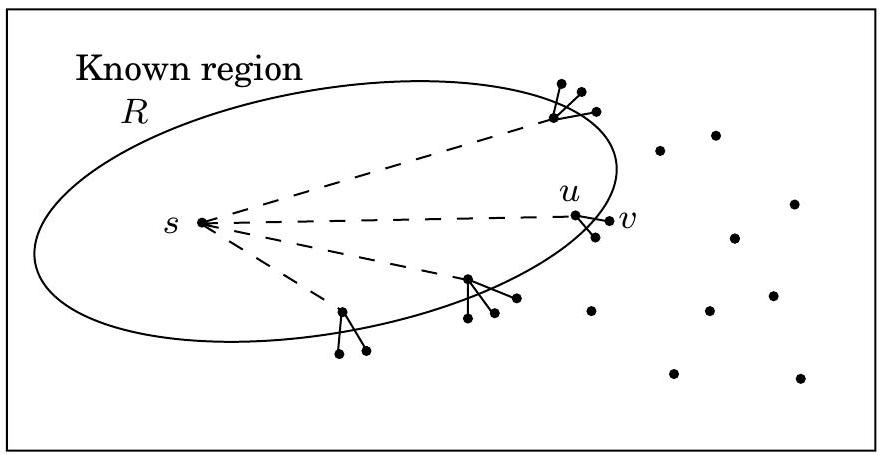
그러나 현재 알려진 최단 경로의 단일 edge 확장은 일반적으로 여러 개가 있을 것이다(Figure 4.10). 이들 중 어떤 것이 를 식별하는가? 답은 이러한 확장된 경로 중 가장 짧은 것이다. 왜냐하면, 만약 더 짧은 단일 edge 확장 경로가 존재한다면, 이는 밖에 있는 에 가장 가까운 노드로서의 의 지위와 다시 한번 모순될 것이기 때문이다. 따라서 를 찾는 것은 쉽다: 가 의 모든 노드를 포함할 때, 의 가장 작은 값이 달성되는 밖의 노드가 이다. 다시 말해, 현재 알려진 최단 경로의 모든 단일 edge 확장을 시도하고, 가장 짧은 확장 경로를 찾아 그 끝점을 의 다음 노드로 선언한다.
이제 현재 최단 경로 집합의 확장을 살펴봄으로써 을 확장하는 알고리즘을 갖게 되었다. 어떤 주어진 반복에서, 유일한 새로운 확장은 가장 최근에 영역 에 추가된 노드를 포함하는 확장이라는 점을 알아차리면 추가적인 효율성을 얻을 수 있다. 다른 모든 확장은 이전에 평가되었으므로 다시 계산할 필요가 없다. 다음 의사 코드에서, 는 로 이어지는 현재 가장 짧은 단일 edge 확장 경로의 길이이다; 에 인접하지 않은 노드의 경우 이다.
Initialize dist(s) to 0 , other dist(.) values to \(\infty\)
\(R=\{ \}\) (the "known regionf)
while \(R \neq V\) :
Pick the node \(v \notin R\) with smallest dist \((\cdot)\)
Add \(v\) to \(R\)
for all edges \((v, z) \in E\) :
if dist( \(z\) ) > dist ( \(v\) ) \(+l(v, z)\) :
\(\operatorname{dist}(z)=\operatorname{dist}(v)+l(v, z)\)
우선순위 큐(priority queue) 연산을 통합하면 Dijkstra's algorithm (Figure 4.8)으로 돌아간다.
이 알고리즘을 공식적으로 정당화하기 위해, 너비 우선 탐색(breadth-first search)과 마찬가지로 귀납법을 사용하여 증명할 것이다. 적절한 귀납적 가설은 다음과 같다.
while 루프의 각 반복이 끝날 때마다 다음 조건이 충족된다: (1) 의 모든 노드는 로부터의 거리가 이고 밖의 모든 노드는 로부터의 거리가 인 값 가 존재한다. (2) 모든 노드 에 대해, 값은 중간 노드가 에 포함되도록 제한된 에서 까지의 최단 경로의 길이이다 (만약 그러한 경로가 존재하지 않으면 값은 이다).
기본 사례는 간단하며(), 귀납 단계의 세부 사항은 앞선 논의에서 채워 넣을 수 있다.
4.4.3 Running time
그림 4.8의 추상화 수준에서 Dijkstra 알고리즘은 너비 우선 탐색(BFS)과 구조적으로 동일하다. 그러나 우선순위 큐(priority queue)의 기본 연산이 BFS의 상수 시간(constant-time) eject 및 inject 연산보다 계산적으로 더 많은 비용을 요구하기 때문에 더 느리다. makequeue는 최대 개의 insert 연산만큼의 시간이 소요되므로, 총 개의 deletemin 연산과 개의 insert/decreasekey 연산이 발생한다. 이러한 연산에 필요한 시간은 구현에 따라 다르다. 예를 들어, **이진 힙(binary heap)을 사용하면 전체 실행 시간은 **가 된다.
4.5 Priority queue implementations
4.5.1 Array
우선순위 큐의 가장 간단한 구현은 모든 잠재적 요소(Dijkstra 알고리즘의 경우 그래프의 정점)에 대한 키 값의 정렬되지 않은 배열이다. 초기에는 이 값들이 로 설정된다.
Which heap is best?
Dijkstra 알고리즘의 실행 시간은 사용되는 우선순위 큐(priority queue) 구현에 크게 좌우된다. 다음은 일반적인 선택 사항들이다.
| 구현 방식 | deletemin | insert/ decreasekey | deletemin + insert |
|---|---|---|---|
| Array | |||
| Binary heap | |||
| -ary heap | |||
| Fibonacci heap | (amortized) |
예를 들어, 단순한 array 구현도 라는 괜찮은 시간 복잡도를 제공하는 반면, binary heap을 사용하면 를 얻는다. 어느 것이 더 선호될까? 이는 그래프가 **sparse(간선이 적음)**한지 **dense(간선이 많음)**한지에 따라 달라진다. 모든 그래프에서 는 보다 작다. 만약 가 라면, array 구현이 더 빠르다. 반면에 가 아래로 떨어지면 binary heap이 더 선호된다. -ary heap은 binary heap(에 해당)의 일반화이며, 의 함수인 실행 시간을 제공한다. 최적의 선택은 이다. 즉, 최적화를 위해서는 heap의 차수(degree)를 그래프의 평균 차수와 같게 설정해야 한다. 이는 sparse 그래프와 dense 그래프 모두에서 잘 작동한다. 인 매우 sparse한 그래프의 경우, 실행 시간은 binary heap과 마찬가지로 이다. dense 그래프의 경우, 이고 실행 시간은 linked list와 마찬가지로 이다. 마지막으로, 중간 밀도 를 가진 그래프의 경우, 실행 시간은 로 선형적이다!
표의 마지막 줄은 Fibonacci heap이라는 정교한 데이터 구조를 사용한 실행 시간을 보여준다. 효율성은 인상적이지만, 이 데이터 구조는 다른 것들보다 구현하는 데 훨씬 더 많은 노력이 필요하며, 이는 실제 적용에서 매력을 떨어뜨리는 경향이 있다. 우리는 시간 경계의 흥미로운 특징을 언급하는 것 외에는 이에 대해 거의 언급하지 않을 것이다. insert 연산은 다양한 시간을 소요하지만, 알고리즘 전체 과정에서 평균적으로 을 보장한다. 이러한 상황(5장에서 하나를 접하게 될 것)에서 우리는 heap insert의 amortized cost가 이라고 말한다.
insert 또는 decreasekey는 키 값을 조정하는 연산에 불과하므로 빠르다. 반면에 deletemin은 리스트를 선형 시간으로 스캔해야 한다.
4.5.2 Binary heap
여기서 요소들은 **완전 이진 트리(complete binary tree)**에 저장된다. 완전 이진 트리는 각 레벨이 왼쪽에서 오른쪽으로 채워지며, 다음 레벨이 시작되기 전에 현재 레벨이 완전히 채워져야 하는 이진 트리이다. 또한, 특별한 정렬 제약 조건이 적용된다: 트리의 모든 노드의 키 값은 자식 노드의 키 값보다 작거나 같아야 한다. 따라서 특히, 루트(root)는 항상 가장 작은 요소를 포함한다. 예시는 Figure 4.11(a)를 참조하라.
삽입하려면 새 요소를 트리의 맨 아래(사용 가능한 첫 번째 위치)에 배치하고 "bubble up"시킨다. 즉, 부모보다 작으면 둘을 교환하고 반복한다(Figure 4.11 (b)-(d)). 교환 횟수는 트리의 높이와 같거나 그보다 작으며, 개의 요소가 있을 때 트리의 높이는 이다. decreasekey는 요소가 이미 트리에 있다는 점을 제외하고는 유사하며, 현재 위치에서 bubble up시킨다.
deletemin을 수행하려면 루트 값을 반환한다. 이 요소를 힙에서 제거하려면 트리의 마지막 노드(맨 아래 행의 가장 오른쪽 위치)를 가져와 루트에 배치한다. 이를 "sift down"시킨다: 두 자식 중 어느 하나보다 크면 더 작은 자식과 교환하고 반복한다(Figure ). 이 역시 시간이 소요된다.
완전 이진 트리의 규칙성 덕분에 배열을 사용하여 쉽게 표현할 수 있다. 트리 노드에는 자연스러운 순서가 있다: 루트에서 시작하여 각 행 내에서 왼쪽에서 오른쪽으로 이동하는 방식이다. 개의 노드가 있다면, 이 순서는 배열 내에서 의 위치를 지정한다. 노드 번호 의 부모는 이고 자식은 와 이라는 사실을 사용하여(Exercise 4.16), 배열에서 트리를 위아래로 이동하는 것을 쉽게 시뮬레이션할 수 있다.
4.5.3 -ary heap
-ary heap은 노드가 두 개 대신 개의 자식을 가진다는 점을 제외하면 binary heap과 동일하다. 이는 개의 요소를 가진 트리의 높이를 로 줄인다. 따라서 삽입(insert) 연산은 만큼 빨라진다. 그러나 deletemin 연산은 로 약간 더 오래 걸린다 (이유를 아시겠는가?).
binary heap의 배열 표현은 -ary heap으로 쉽게 확장될 수 있다. 이번에는 노드 번호 가 부모 를 가지며, 자식은 , 이다 (연습문제 4.16).
4.6 Shortest paths in the presence of negative edges
4.6.1 Negative edges
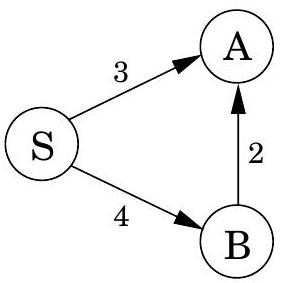
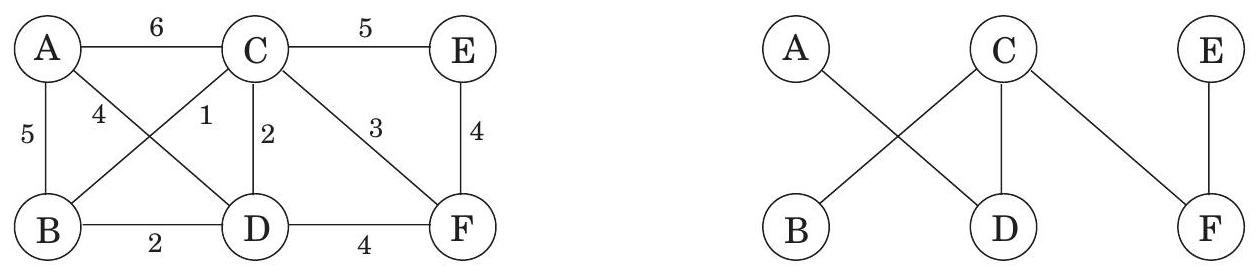
Dijkstra 알고리즘은 시작점 에서 어떤 노드 까지의 최단 경로가 보다 가까운 노드들만을 통과해야 한다는 전제하에 작동한다. 하지만 간선 길이가 음수일 때는 이 전제가 더 이상 유효하지 않다. 그림 4.12에서 에서 까지의 최단 경로는 더 멀리 떨어진 노드인 를 통과한다!
이러한 새로운 복잡성을 수용하기 위해 무엇을 변경해야 할까? 이에 답하기 위해 Dijkstra 알고리즘을 높은 수준에서 살펴보자. 중요한 **불변성(invariant)**은 알고리즘이 유지하는 dist 값이 항상 과대평가되거나 정확하다는 것이다. 이 값들은 에서 시작하며, 변경되는 유일한 방법은 다음과 같이 업데이트하는 것이다.
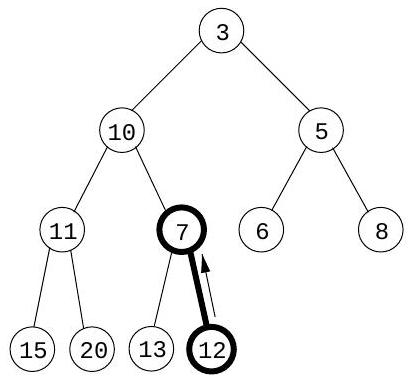
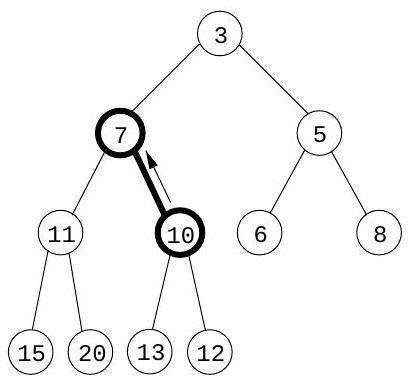
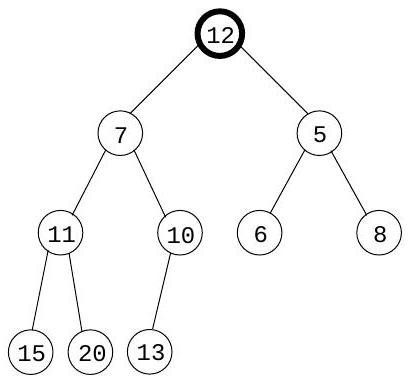
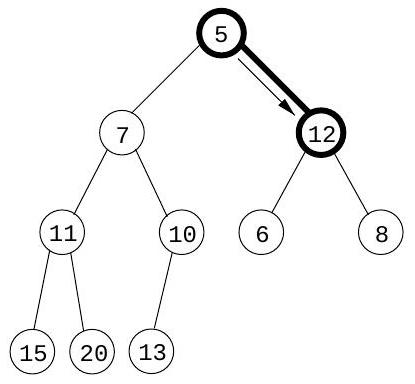
그림 4.11 (a) 10개의 요소를 가진 이진 힙. 키 값만 표시되어 있다. (b)-(d) 키 7을 가진 요소를 삽입할 때의 중간 "bubble-up" 단계. (e)-(g) delete-min 연산 시 "sift-down" 단계.
(a)
(b)
(c)
(d)
(e)

(f)
(g)
(h)
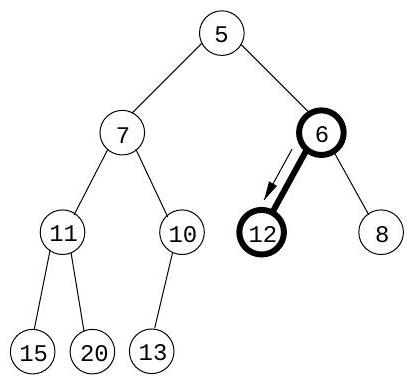
그림 4.12 음수 간선이 있으면 Dijkstra 알고리즘은 작동하지 않는다.
간선을 따라 업데이트하는 것이다:
procedure update \(((u, v) \in E)\)
dist \((v)=\min \{\) dist \((v)\), dist \((u)+l(u, v)\}\)
이 update 연산은 까지의 거리가 까지의 거리와 를 더한 값보다 클 수 없다는 사실을 단순히 표현한 것이다. 이 연산은 다음과 같은 속성을 갖는다.
- 가 로 가는 최단 경로의 마지막에서 두 번째 노드이고, dist()가 정확하게 설정된 특정 경우에 까지의 정확한 거리를 제공한다.
- dist()를 너무 작게 만들지 않으며, 이러한 의미에서 안전하다. 예를 들어, 불필요한 update가 많이 발생해도 해가 되지 않는다.
이 연산은 매우 유용하다: 해롭지 않으며, 신중하게 사용하면 거리를 정확하게 설정할 것이다. 사실, Dijkstra 알고리즘은 단순히 update의 연속으로 생각할 수 있다. 우리는 이 특정 순서가 음수 간선에서는 작동하지 않는다는 것을 알고 있지만, 작동하는 다른 순서가 있을까? 이 순서가 가져야 할 속성을 파악하기 위해 노드 를 선택하고 에서 까지의 최단 경로를 살펴보자.
이 경로는 최대 개의 간선을 가질 수 있다(이유를 아는가?). 수행된 update 시퀀스에 가 그 순서대로(반드시 연속적일 필요는 없지만) 포함된다면, 첫 번째 속성에 의해 까지의 거리가 정확하게 계산될 것이다. 이 간선들에서 다른 어떤 update가 발생하든, 또는 그래프의 나머지 부분에서 어떤 일이 발생하든 상관없다. 왜냐하면 update는 안전하기 때문이다.
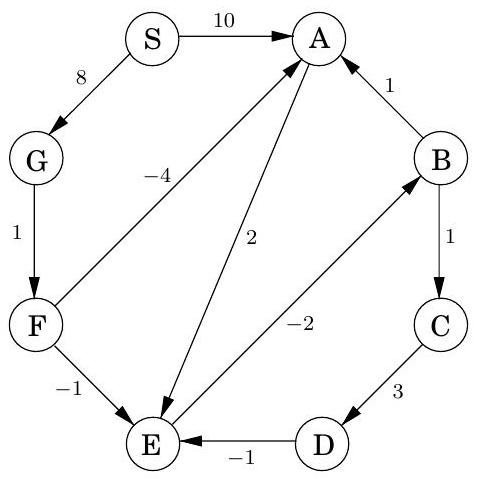
하지만 여전히 모든 최단 경로를 미리 알지 못한다면, 올바른 간선을 올바른 순서로 업데이트하는 방법을 어떻게 확신할 수 있을까? 여기에 쉬운 해결책이 있다: 단순히 모든 간선을 번 업데이트하는 것이다! 결과적으로 절차를 Bellman-Ford 알고리즘이라고 하며, 그림 4.13에 나와 있고, 예시 실행은 그림 4.14에 나와 있다.
그림 4.13 일반 그래프에서 단일 소스 최단 경로를 찾는 Bellman-Ford 알고리즘.
procedure shortest-paths ( G, l,s)
Input: Directed graph G = (V,E);
edge lengths {le:e\inE} with no negative cycles;
vertex s\inV
Output:For all vertices u reachable from s, dist(u) is set
to the distance from s to u.
for all u\inV:
dist(u)=\infty
prev(u) = nil
dist(s)=0
repeat |V|-1 times:
for all e\inE:
update(e)
그림 4.14 샘플 그래프에서 Bellman-Ford 알고리즘을 설명한다.
| Iteration | ||||||||
|---|---|---|---|---|---|---|---|---|
| Node | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| S | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| A | 10 | 10 | 5 | 5 | 5 | 5 | 5 | |
| B | 10 | 6 | 5 | 5 | 5 | |||
| C | 11 | 7 | 6 | 6 | ||||
| D | 14 | 10 | 9 | |||||
| E | 12 | 8 | 7 | 7 | 7 | 7 | ||
| F | 9 | 9 | 9 | 9 | 9 | 9 | ||
| G | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
구현에 대한 참고: 많은 그래프에서 어떤 최단 경로의 최대 간선 수는 보다 훨씬 적으며, 결과적으로 더 적은 수의 update 라운드가 필요하다. 따라서 최단 경로 알고리즘에 추가 검사를 추가하여, update가 발생하지 않은 라운드 직후에 즉시 종료되도록 하는 것이 합리적이다.
4.6.2 Negative cycles
그림 4.14에서 엣지 ()의 길이가 -4로 변경되면, 그래프는 와 같은 **음수 사이클(negative cycle)**을 갖게 된다. 이러한 상황에서는 최단 경로에 대해 묻는 것 자체가 의미가 없다. 에서 까지 길이가 2인 경로가 있지만, 사이클을 한 바퀴 돌면 길이가 1인 경로도 있고, 여러 번 돌면 길이가 등인 경로를 찾을 수 있다.
**최단 경로 문제(shortest-path problem)**는 음수 사이클이 있는 그래프에서는 **잘못 설정된 문제(ill-posed)**이다. 예상할 수 있듯이, 섹션 4.6.1의 알고리즘은 이러한 사이클이 없는 경우에만 작동한다. 그렇다면 이 가정이 알고리즘 도출 과정에서 어디에 나타났을까? 이는 에서 까지의 최단 경로가 존재한다고 주장했을 때 슬그머니 포함되었다.
다행히도 음수 사이클을 자동으로 감지하고 경고를 발행하는 것은 쉽다. 이러한 사이클은 update operation을 끝없이 적용하여 매번 dist estimate를 줄일 수 있게 한다. 따라서 번의 반복 후에 멈추는 대신, 한 번의 추가 라운드를 수행한다. 이 마지막 라운드 동안 일부 dist 값이 감소한다면, 그리고 그 경우에만 음수 사이클이 존재한다.
4.7 Shortest paths in dags
음수 사이클의 가능성을 자동으로 배제하는 그래프에는 두 가지 하위 클래스가 있다: 음수 간선이 없는 그래프와 사이클이 없는 그래프. 우리는 전자를 효율적으로 처리하는 방법을 이미 알고 있다. 이제 **방향성 비순환 그래프(DAG)**에서 단일-소스 최단 경로 문제를 선형 시간 내에 해결하는 방법을 살펴볼 것이다.
이전과 마찬가지로, 모든 최단 경로를 부분 시퀀스로 포함하는 일련의 업데이트를 수행해야 한다. 효율성의 핵심 원천은 다음과 같다:
DAG의 모든 경로에서 정점들은 선형화된 순서대로 나타난다.
그림 4.15 방향성 비순환 그래프를 위한 단일-소스 최단 경로 알고리즘.
procedure dag-shortest-paths ( G,l,s)
Input: Dag G = (V,E);
edge lengths {le:e\inE}; vertex s\inV
Output:For all vertices u reachable from s, dist(u) is set
to the distance from s to u.
for all u\inV:
dist(u)=\infty
prev(u)= nil
dist(s)=0
Linearize G
for each u\inV, in linearized order:
for all edges (u,v)\inE:
update(u,v)
따라서 **깊이 우선 탐색(DFS)**을 통해 DAG를 선형화(즉, 위상 정렬)한 다음, 정렬된 순서대로 정점들을 방문하면서 각 정점에서 나가는 간선들을 업데이트하는 것으로 충분하다. 이 알고리즘은 그림 4.15에 제시되어 있다.
우리의 방식은 간선이 양수일 것을 요구하지 않는다는 점에 주목하라. 특히, 모든 간선 길이를 음수로 바꾸면 동일한 알고리즘으로 DAG에서 최장 경로를 찾을 수 있다.
Exercises
4.1. 다음 그래프에서 노드 부터 시작하여 Dijkstra 알고리즘을 실행한다고 가정한다.
 (a) 알고리즘의 각 iteration에서 모든 노드의 중간 거리 값을 보여주는 표를 작성하시오.
(b) 최종 최단 경로 트리를 보여주시오.
4.2. 이전 문제와 동일하지만, 이번에는 Bellman-Ford 알고리즘을 사용한다.
(a) 알고리즘의 각 iteration에서 모든 노드의 중간 거리 값을 보여주는 표를 작성하시오.
(b) 최종 최단 경로 트리를 보여주시오.
4.2. 이전 문제와 동일하지만, 이번에는 Bellman-Ford 알고리즘을 사용한다.
 4.3. 사각형. 무방향 그래프 를 입력으로 받아 길이가 4인 단순 사이클(즉, 자기 자신과 교차하지 않는 사이클)을 포함하는지 여부를 결정하는 알고리즘을 설계하고 분석하시오. 실행 시간은 최대 이어야 한다.
4.3. 사각형. 무방향 그래프 를 입력으로 받아 길이가 4인 단순 사이클(즉, 자기 자신과 교차하지 않는 사이클)을 포함하는지 여부를 결정하는 알고리즘을 설계하고 분석하시오. 실행 시간은 최대 이어야 한다.
입력 그래프는 인접 행렬 또는 인접 리스트 중 알고리즘을 더 간단하게 만드는 방식으로 표현된다고 가정할 수 있다. 4.4. 단위 에지 길이를 가진 무방향 그래프에서 최단 사이클의 길이를 찾는 방법에 대한 제안이 있다.
깊이 우선 탐색(DFS) 중에 백 에지(예: )가 발견되면, 에서 로 가는 트리 에지와 함께 사이클을 형성한다. 사이클의 길이는 level 이며, 여기서 정점의 level은 DFS 트리에서 루트 정점으로부터의 거리이다. 이는 다음 알고리즘을 제안한다:
- 각 정점의 level을 추적하면서 깊이 우선 탐색을 수행한다.
- 백 에지가 발견될 때마다 사이클 길이를 계산하고, 이전에 본 최단 길이보다 작으면 저장한다. 이 전략이 항상 작동하지 않음을 반례와 간략한 (한두 문장) 설명으로 보여주시오. 4.5. 그래프의 두 노드 사이에 여러 최단 경로가 있는 경우가 종종 있다. 다음 task에 대한 선형 시간 알고리즘을 제시하시오.
입력: 단위 에지 길이를 가진 무방향 그래프 ; 노드 .
출력: 에서 까지의 서로 다른 최단 경로의 수.
4.6. Dijkstra 알고리즘에 의해 계산된 배열 prev에 대해, 에지 (모든 에 대해)가 트리를 형성함을 증명하시오.
4.7. (음수일 수 있는) 가중치 에지를 가진 방향 그래프 와 특정 노드 , 그리고 트리 가 주어진다. 가 시작점 를 가진 의 최단 경로 트리인지 확인하는 알고리즘을 제시하시오. 알고리즘은 선형 시간으로 실행되어야 한다.
4.8. F. Lake 교수는 일부 음수 에지를 가진 방향 그래프에서 노드 에서 노드 까지의 최단 경로를 찾는 다음 알고리즘을 제안한다: 각 에지 가중치에 큰 상수를 더하여 모든 가중치가 양수가 되도록 한 다음, 노드 에서 시작하여 Dijkstra 알고리즘을 실행하고, 노드 까지 발견된 최단 경로를 반환한다.
이것이 유효한 방법인가? 올바르게 작동함을 증명하거나, 반례를 제시하시오. 4.9. 에서 나가는 에지만 음수이고 다른 모든 에지는 양수인 방향 그래프를 고려한다. 에서 시작된 Dijkstra 알고리즘이 이러한 그래프에서 실패할 수 있는가? 답을 증명하시오. 4.10. (음수일 수 있는) 가중치 에지를 가진 방향 그래프가 주어지며, 임의의 두 정점 사이의 최단 경로는 최대 개의 에지를 가짐이 보장된다. 두 정점 와 사이의 최단 경로를 시간에 찾는 알고리즘을 제시하시오. 4.11. 양수 에지 길이를 가진 방향 그래프를 입력으로 받아 그래프의 최단 사이클 길이를 반환하는 알고리즘을 제시하시오 (그래프가 비순환이면 그렇게 말해야 한다). 알고리즘은 최대 시간이 소요되어야 한다. 4.12. 다음 task에 대한 알고리즘을 제시하시오.
입력: 무방향 그래프 ; 에지 길이 ; 에지 . 출력: 에지 를 포함하는 최단 사이클의 길이. 4.13. 도시 집합과 그 사이의 고속도로 패턴이 무방향 그래프 형태로 주어진다. 고속도로의 각 구간 는 두 도시를 연결하며, 그 길이는 마일 단위로 이다. 도시 에서 도시 로 가려고 한다. 한 가지 문제가 있다: 자동차는 마일을 커버할 수 있는 충분한 연료만 담을 수 있다. 각 도시에는 주유소가 있지만 도시 사이에는 없다. 따라서 모든 에지의 길이가 인 경로만 이용할 수 있다. (a) 자동차 연료 탱크 용량의 제한을 고려하여, 에서 까지 실행 가능한 경로가 있는지 선형 시간으로 결정하는 방법을 보여주시오. (b) 이제 새 차를 구입할 계획이며, 에서 까지 이동하는 데 필요한 최소 연료 탱크 용량을 알고 싶다. 이를 결정하는 알고리즘을 제시하시오. 4.14. 양수 에지 가중치를 가진 강하게 연결된 방향 그래프 와 특정 노드 가 주어진다. 모든 노드 쌍 사이의 최단 경로를 찾는 효율적인 알고리즘을 제시하시오. 단, 이 경로들은 모두 를 통과해야 한다는 한 가지 제약이 있다. 4.15. 최단 경로는 항상 유일하지는 않다: 때로는 가능한 최소 길이의 두 개 이상의 다른 경로가 있다. 다음 문제를 시간에 해결하는 방법을 보여주시오.
입력: 무방향 그래프 ; 에지 길이 ; 시작 정점 .
출력: 부울 배열 usp[:]: 각 노드 에 대해, usp[u] 항목은 에서 까지의 유일한 최단 경로가 있을 때만 참이어야 한다. (참고:
4.16. 섹션 4.5.2에서는 개의 노드를 가진 완전 이진 트리를 으로 인덱싱된 배열에 저장하는 방법을 설명한다.
(a) 배열의 위치에 있는 노드를 고려한다. 그 부모는 위치에 있고 자식은 와 위치에 있음을 보여주시오 (이 숫자들이 인 경우).
(b) 완전 -ary 트리가 배열에 저장될 때 해당하는 인덱스는 무엇인가?
그림 4.16은 R. E. Tarjan의 설명을 모델로 한 이진 힙의 의사 코드를 보여준다. 힙은 배열 로 저장되며, 두 가지 상수 시간 연산을 지원한다고 가정한다:
- : 현재 배열에 있는 요소의 수를 반환한다.
- : 배열 내 요소의 위치를 반환한다.
후자는 보조 배열로 의 값을 유지함으로써 항상 달성할 수 있다.
(c) makeheap 프로시저가 개의 요소 집합에 대해 호출될 때 시간이 소요됨을 보여주시오. 최악의 입력은 무엇인가? (힌트: 실행 시간이 최대 임을 보여주는 것부터 시작하시오.)
(d) 이 의사 코드를 -ary 힙에 적용하기 위해 무엇을 변경해야 하는가?
그림 4.16 이진 힙에 대한 연산.
procedure insert(h,x)
bubbleup(h, x, |h| + 1)
procedure decreasekey(h,x)
bubbleup(h,x,h-1(x))
function deletemin (h)
if |h|=0:
return null
else:
x = h(1)
siftdown (h,h(|h|), 1)
return x
function makeheap(S)
h=empty array of size |S|
for x\inS:
h ( | h | + 1 ) = x
for i=|S| downto 1:
siftdown (h,h(i),i)
return h
procedure bubbleup(h,x,i)
(place element x in position i of h, and let it bubble up)
p=\lceilі/2\rceil
while ifl and key (h(p)) > key(x):
h(i) = h(p); i= p; p = \lceili/2\rceil
h(i) = x
procedure siftdown (h,x,i)
(place element x in position i of h, and let it sift down)
c=minchild(h,i)
while cf=0 and key(h(c))<key(x):
h(i)=h(c); i=c; c=minchild(h,i)
h(i) = x
function minchild(h,i)
(return the index of the smallest child of h(i))
if 2i>|h|:
return 0 (no children)
else:
return argmin{key(h(j)):2i\leqj\leqmin{|h|,2i+1}}
4.17. 에지 가중치가 범위의 정수이고 가 비교적 작은 숫자인 그래프에서 Dijkstra 알고리즘을 실행한다고 가정한다.
(a) Dijkstra 알고리즘이 시간에 실행되도록 하는 방법을 보여주시오.
(b) 시간만 소요되는 대체 구현을 보여주시오.
4.18. 두 노드 사이에 여러 최단 경로가 있는 경우 (그리고 에지 길이가 다양한 경우), 이 경로들 중 가장 편리한 경로는 종종 에지 수가 가장 적은 경로이다. 예를 들어, 노드가 도시를 나타내고 에지 길이가 도시 간 비행 비용을 나타내는 경우, 도시 에서 도시 로 가는 많은 방법이 모두 동일한 비용을 가질 수 있다. 이러한 대안 중 가장 편리한 것은 경유지가 가장 적은 경로이다. 따라서 특정 시작 노드 에 대해 다음을 정의한다:
best 에서 까지의 최단 경로에서 최소 에지 수.
아래 예에서 노드 에 대한 best 값은 각각 이다.
다음 문제에 대한 효율적인 알고리즘을 제시하시오.
입력: 그래프 ; 양수 에지 길이 ; 시작 노드 .
출력: 모든 노드 에 대해 best[u] 값이 설정되어야 한다.
4.19. 일반화된 최단 경로 문제. 인터넷 라우팅에서는 회선 지연뿐만 아니라 라우터에서의 지연이 더 중요하다. 이는 일반화된 최단 경로 문제를 유발한다.
에지 길이 외에도 그래프에 정점 비용 이 있다고 가정한다. 이제 경로의 비용을 에지 길이의 합과 경로상의 모든 정점 (종점 포함)의 비용의 합으로 정의한다. 다음 문제에 대한 효율적인 알고리즘을 제시하시오.
입력: 방향 그래프 ; 양수 에지 길이 및 양수 정점 비용 ; 시작 정점 .
출력: 모든 정점 에 대해 cost[u]가 위 정의에 따라 에서 까지의 모든 경로 중 가장 적은 비용 (즉, 가장 저렴한 경로의 비용)인 배열 cost[:].
cost[s]=c_s임을 주목하시오.
4.20. 도시 집합 를 연결하는 도로 네트워크 가 있다. 의 각 도로는 관련 길이 를 가진다. 이 네트워크에 하나의 새 도로를 추가하려는 제안이 있으며, 새 도로를 건설할 수 있는 도시 쌍의 목록 가 있다. 이러한 각 잠재적 도로 에는 관련 길이가 있다. 공공 사업 부서의 설계자로서 기존 네트워크 에 추가될 때 네트워크의 두 고정 도시 와 사이의 운전 거리가 최대 감소를 가져올 도로 를 결정하도록 요청받았다. 이 문제를 해결하기 위한 효율적인 알고리즘을 제시하시오.
4.21. 최단 경로 알고리즘은 통화 거래에 적용될 수 있다. 을 다양한 통화라고 하자; 예를 들어, 은 달러, 는 파운드, 는 엔일 수 있다. 임의의 두 통화 와 에 대해 환율 가 있다; 이는 1단위와 교환하여 단위를 구매할 수 있음을 의미한다. 이 환율은 조건을 만족한다. 따라서 1단위로 시작하여 로 변경한 다음 다시 로 변환하면 1단위 미만으로 끝나게 된다 (차액은 거래 비용이다).
(a) 다음 문제에 대한 효율적인 알고리즘을 제시하시오: 주어진 환율 집합 와 두 통화 및 에 대해, 통화 를 통화 로 변환하는 가장 유리한 통화 교환 시퀀스를 찾으시오. 이 목표를 위해 통화와 환율을 에지 길이가 실수인 그래프로 표현해야 한다.
환율은 다양한 통화의 수요와 공급을 반영하여 자주 업데이트된다. 때때로 환율은 다음 속성을 만족한다: 인 통화 시퀀스 가 있다. 이는 1단위로 시작하여 차례로 로 변환한 다음 마지막으로 로 다시 변환하면 1단위 이상으로 끝나게 됨을 의미한다. 이러한 이상 현상은 외환 시장에서 1분도 채 지속되지 않지만, 무위험 이익을 얻을 기회를 제공한다. (b) 이러한 이상 현상의 존재를 감지하기 위한 효율적인 알고리즘을 제시하시오. 위에서 찾은 그래프 표현을 사용하시오. 4.22. 떠돌이 증기선 문제. 당신은 항구 도시 그룹 사이를 운항할 수 있는 증기선 소유주이다. 각 항구에서 돈을 번다: 도시 를 방문하면 달러의 이익을 얻는다. 한편, 항구 에서 항구 까지의 운송 비용은 이다. 이익 대 비용의 비율이 최대화되는 순환 경로를 찾고자 한다.
이를 위해 노드가 항구이고 각 항구 쌍 사이에 에지가 있는 방향 그래프 를 고려한다. 이 그래프의 임의의 사이클 에 대해 이익 대 비용 비율은 다음과 같다.
를 단순 사이클로 달성할 수 있는 최대 비율이라고 하자. 를 결정하는 한 가지 방법은 이진 탐색이다: 먼저 어떤 비율 을 추측한 다음, 너무 크거나 너무 작은지 테스트한다.
임의의 양수 을 고려한다. 각 에지 에 의 가중치를 부여한다. (a) 음수 가중치의 사이클이 있으면 임을 보여주시오. (b) 그래프의 모든 사이클이 엄격하게 양수 가중치를 가지면 임을 보여주시오. (c) 원하는 정확도 을 입력으로 받아 인 단순 사이클 를 반환하는 효율적인 알고리즘을 제시하시오. 알고리즘의 정확성을 정당화하고 , 그리고 측면에서 실행 시간을 분석하시오.
Chapter 5
Greedy algorithms
체스와 같은 게임은 미리 생각해야만 이길 수 있다. 즉각적인 이점에만 전적으로 집중하는 플레이어는 쉽게 패배한다. 그러나 스크래블과 같은 다른 많은 게임에서는 당장 가장 좋아 보이는 수를 두고 미래의 결과에 대해 너무 걱정하지 않음으로써 꽤 잘할 수 있다.
이러한 종류의 **근시안적인 행동(myopic behavior)**은 쉽고 편리하여 매력적인 알고리즘 전략이 된다. **그리디 알고리즘(greedy algorithms)**은 가장 명확하고 즉각적인 이점을 제공하는 다음 조각을 항상 선택하면서 솔루션을 조각별로 구축한다. 이러한 접근 방식은 일부 계산 작업에서는 치명적일 수 있지만, 최적의 결과를 제공하는 경우도 많다. 첫 번째 예시는 **최소 신장 트리(minimum spanning trees)**이다.
5.1 Minimum spanning trees
일련의 컴퓨터들을 선택된 쌍으로 연결하여 네트워크를 구성해야 한다고 가정해 보자. 이는 노드가 컴퓨터이고, 무방향 에지가 잠재적 링크이며, 노드들이 연결되도록 충분한 에지를 선택하는 것이 목표인 그래프 문제로 해석된다. 하지만 이것이 전부가 아니다. 각 링크에는 유지보수 비용이 있으며, 이는 해당 에지의 **가중치(weight)**로 반영된다. 가장 저렴한 네트워크는 무엇일까?
한 가지 즉각적인 관찰은 최적의 에지 집합이 **사이클(cycle)**을 포함할 수 없다는 것이다. 왜냐하면 이 사이클에서 에지 하나를 제거하면 연결성을 손상시키지 않으면서 비용을 줄일 수 있기 때문이다.
속성 1 사이클 에지를 제거해도 그래프의 연결이 끊어지지 않는다. 따라서 해답은 연결되어 있고 비순환적이어야 한다. 이러한 종류의 무방향 그래프를 **트리(tree)**라고 한다. 우리가 원하는 특정 트리는 총 가중치가 최소인 트리이며, 이를 **최소 신장 트리(minimum spanning tree)**라고 한다. 다음은 그 공식적인 정의이다.
입력: 무방향 그래프 ; 에지 가중치 . 출력: 를 만족하는 트리 로, 다음을 최소화한다.
위 예시에서 최소 신장 트리의 비용은 16이다:
하지만 이것이 유일한 최적 해답은 아니다. 다른 해답을 찾을 수 있는가?
5.1.1 A greedy approach
Kruskal의 최소 신장 트리 알고리즘은 빈 그래프에서 시작하여 다음 규칙에 따라 에서 edge를 선택한다.
cycle을 생성하지 않는 다음으로 가벼운 edge를 반복적으로 추가한다. 다시 말해, 이 알고리즘은 edge를 하나씩 구성하며, cycle을 피하는 것 외에는 현재 가장 저렴한 edge를 선택한다. 이는 **탐욕 알고리즘(greedy algorithm)**이다. 즉, 알고리즘이 내리는 모든 결정은 가장 명백하고 즉각적인 이점을 가진 결정이다.
그림 5.1은 예시를 보여준다. 우리는 빈 그래프에서 시작하여 가중치 증가 순서로 edge를 추가하려고 시도한다(동점은 임의로 처리한다):
처음 두 edge는 성공적으로 추가되지만, 세 번째 edge인 는 추가될 경우 cycle을 생성한다. 따라서 우리는 이를 무시하고 다음 edge로 넘어간다. 최종 결과는 비용이 14인 트리이며, 이는 가능한 최소 비용이다.
그림 5.1 Kruskal 알고리즘으로 찾은 최소 신장 트리.
Trees
트리는 연결되어 있고 비순환적인 무방향 그래프이다. 트리가 유용한 주된 이유는 그 구조의 단순성 때문이다. 예를 들어,
속성 2 개의 노드를 가진 트리는 개의 edge를 가진다. 이는 빈 그래프에서 시작하여 한 번에 하나의 edge를 추가하면서 트리를 구축함으로써 알 수 있다. 처음에는 개의 각 노드가 다른 노드들과 단절되어, 그 자체로 연결된 컴포넌트를 이룬다. edge가 추가됨에 따라 이 컴포넌트들은 병합된다. 각 edge는 두 개의 다른 컴포넌트를 결합하므로, 트리가 완전히 형성될 때까지 정확히 개의 edge가 추가된다.
좀 더 자세히 설명하자면: 특정 edge 가 나타날 때, 와 가 서로 다른 연결된 컴포넌트에 있다는 것을 확신할 수 있다. 만약 그렇지 않다면 이미 그들 사이에 경로가 존재하여 이 edge가 cycle을 생성할 것이기 때문이다. edge를 추가하면 이 두 컴포넌트가 병합되어 전체 연결된 컴포넌트의 수가 하나 줄어든다. 이 점진적인 과정 동안 컴포넌트의 수는 개에서 1개로 감소하며, 이는 그 과정에서 개의 edge가 추가되었음을 의미한다. 역도 또한 참이다. 속성 3 인 모든 연결된 무방향 그래프 는 트리이다. 우리는 가 비순환적임을 보여주기만 하면 된다. 이를 수행하는 한 가지 방법은 다음과 같은 반복 절차를 실행하는 것이다: 그래프에 cycle이 포함되어 있는 동안, 이 cycle에서 하나의 edge를 제거한다. 이 과정은 비순환적이며, 속성 1(127페이지)에 의해 연결된 그래프 로 종료된다. 따라서 는 트리이며, 속성 2에 의해 이다. 그러므로 이고, 제거된 edge는 없으며, 는 처음부터 비순환적이었다.
다시 말해, 연결된 그래프가 트리인지 여부는 edge의 개수를 세는 것만으로 알 수 있다. 다음은 또 다른 특징이다. 속성 4 무방향 그래프는 임의의 두 노드 사이에 유일한 경로가 있을 때 그리고 그 때에만 트리이다.
트리에서는 임의의 두 노드 사이에 하나의 경로만 존재할 수 있다. 만약 두 개의 경로가 있다면, 이 경로들의 합집합은 cycle을 포함할 것이기 때문이다.
반면에, 그래프가 임의의 두 노드 사이에 경로를 가지고 있다면, 그것은 연결되어 있다. 만약 이 경로들이 유일하다면, 그래프는 또한 비순환적이다(cycle은 임의의 두 노드 사이에 두 개의 경로를 가지므로).
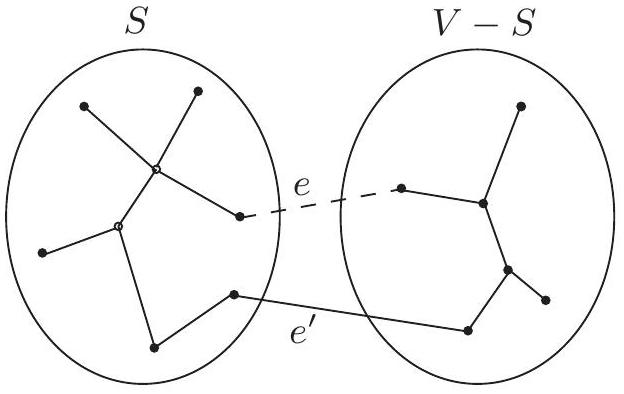
그림 5.2 . (실선)에 (점선)를 추가하면 cycle이 생성된다. 이 cycle은 cut()을 가로지르는 적어도 하나의 다른 edge, 여기서는 로 표시된 edge를 포함해야 한다.
Kruskal의 방법의 정확성은 특정 cut 속성에서 비롯되며, 이 속성은 다른 많은 최소 신장 트리 알고리즘을 정당화할 만큼 충분히 일반적이다.
5.1.2 The cut property
최소 신장 트리(MST)를 구축하는 과정에서 이미 일부 간선(edge)을 선택했고, 지금까지 올바른 방향으로 진행되고 있다고 가정해 보자. 다음으로 어떤 간선을 추가해야 할까? 다음 보조정리는 선택에 있어 많은 유연성을 제공한다.
Cut property 간선 집합 가 의 최소 신장 트리의 일부라고 가정하자. 가 와 사이를 가로지르지 않는 노드들의 부분집합 를 임의로 선택하고, 이 분할(partition)을 가로지르는 가장 가벼운 간선을 라고 하자. 그러면 는 어떤 MST의 일부이다.
Cut은 정점들을 두 그룹 와 로 분할하는 것을 의미한다. 이 속성이 말하는 바는, 가 cut을 가로지르는 간선을 가지고 있지 않다면, 어떤 cut을 가로지르는 가장 가벼운 간선(즉, 의 정점과 의 정점 사이의 간선)을 추가하는 것은 항상 안전하다는 것이다.
이것이 왜 성립하는지 살펴보자. 간선 집합 는 어떤 MST 의 일부이다. 만약 새로운 간선 도 의 일부라면 증명할 필요가 없다. 따라서 가 에 없다고 가정하자. 우리는 를 약간 변경하여, 단 하나의 간선만 바꾸어 를 포함하는 다른 MST 를 구성할 것이다.
간선 를 에 추가하자. 는 연결되어 있으므로, 의 양 끝점 사이에 이미 경로가 존재하며, 를 추가하면 사이클이 생성된다. 이 사이클은 cut ()을 가로지르는 다른 간선 도 포함해야 한다(Figure 5.2). 이제 이 간선을 제거하면 가 남게 되는데, 이것이 트리임을 보일 것이다. 는 사이클 간선이므로, 속성 1에 의해 는 연결되어 있다. 그리고 와 동일한 수의 간선을 가지므로, 속성 2와 3에 의해 또한 트리이다.
더욱이 는 최소 신장 트리이다. 의 가중치를 의 가중치와 비교해 보자:
Figure 5.3 cut property의 작동 예시. (a) 무방향 그래프. (b) 집합 는 세 개의 간선을 가지며, 오른쪽에 있는 MST 의 일부이다. (c) 만약 라면, cut ()을 가로지르는 최소 가중치 간선 중 하나는 이다. 는 오른쪽에 표시된 MST 의 일부이다.
(a)
(b)
:
(c)
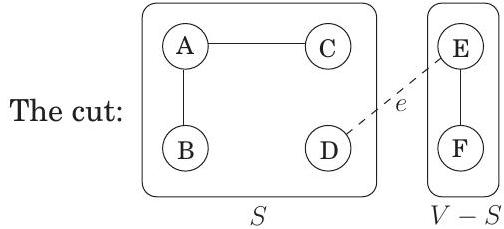
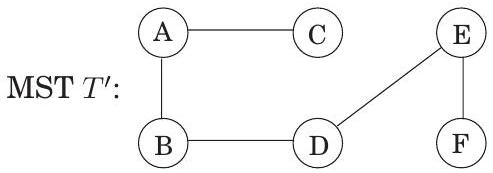
와 모두 와 사이를 가로지르며, 는 특히 이 유형의 간선 중 가장 가벼운 간선이다. 따라서 이고, weight weight 이다. 가 MST이므로, weight weight 여야 하며 또한 MST이다.
Figure 5.3은 cut property의 예시를 보여준다. 는 어떤 간선인가?
5.1.3 Kruskal's algorithm
이제 Kruskal 알고리즘을 정당화할 준비가 되었다. 어떤 시점에서든, 이 알고리즘이 이미 선택한 edge들은 부분 해(partial solution)를 형성하는데, 이는 각각 트리 구조를 가진 연결된 컴포넌트들의 집합이다. 다음에 추가될 edge 는 이 컴포넌트들 중 두 개를 연결한다. 이들을 과 라고 부르자. 는 cycle을 생성하지 않는 가장 가벼운 edge이므로, 과 사이에서 가장 가벼운 edge임이 확실하며, 따라서 cut property를 만족한다.
이제 몇 가지 구현 세부 사항을 살펴보자. 각 단계에서 알고리즘은 현재의 부분 해에 추가할 edge를 선택한다. 이를 위해 각 후보 edge 에 대해 endpoint 와 가 서로 다른 컴포넌트에 속하는지 테스트해야 한다. 그렇지 않으면 해당 edge는 cycle을 생성한다. 그리고 edge가 선택되면 해당 컴포넌트들을 병합해야 한다. 어떤 종류의 데이터 구조가 이러한 연산을 지원할까?
그림 5.4 Kruskal의 최소 신장 트리 알고리즘.
procedure kruskal (G, w)
Input: 가중치 we를 가진 연결된 무방향 그래프 G = (V,E)
output: edge X로 정의된 최소 신장 트리
for all u\inV:
makeset (u)
X= {}
sort the edges E by weight
for all edges {u,v}\inE, in increasing order of weight:
if find(u) \not= find(v):
add edge {u,v} to X
union(u,v)
우리는 알고리즘의 상태를 disjoint sets의 집합으로 모델링할 것이다. 각 집합은 특정 컴포넌트의 노드들을 포함한다. 초기에는 각 노드가 자체적으로 컴포넌트에 속한다: makeset : 만을 포함하는 단일 집합을 생성한다. 우리는 노드 쌍들이 같은 집합에 속하는지 반복적으로 테스트한다. find : 는 어떤 집합에 속하는가? 그리고 edge를 추가할 때마다 두 컴포넌트를 병합한다. union : 와 를 포함하는 집합들을 병합한다. 최종 알고리즘은 그림 5.4에 나와 있다. 이 알고리즘은 개의 makeset, 개의 find, 그리고 개의 union 연산을 사용한다.
5.1.4 A data structure for disjoint sets
Union by rank:
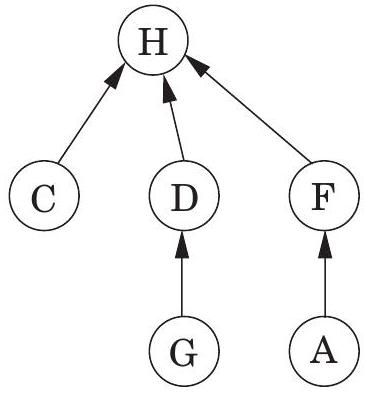
집합을 저장하는 한 가지 방법은 **방향성 트리(directed tree)**로 저장하는 것이다(Figure 5.5). 트리의 노드는 집합의 요소이며, 특별한 순서 없이 배열되고, 각 노드는 결국 트리의 **루트(root)**로 이어지는 부모 포인터를 가지고 있다. 이 루트 요소는 집합의 편리한 대표자, 즉 이름이 된다. 루트는 부모 포인터가 자기 자신을 가리키는 self-loop라는 사실로 다른 요소들과 구별된다.
부모 포인터 외에도 각 노드는 rank를 가지고 있으며, 이는 현재로서는 해당 노드에서 뻗어 나가는 서브트리의 높이로 해석되어야 한다.
procedure makeset(x)
\pi(x)=x
rank(x)=0
function find(x)
while xfl}=\pi(x):\quadx=\pi(x)
return x
Figure 5.5 두 집합 와 의 방향성 트리 표현.

예상할 수 있듯이, makeset은 상수 시간(constant-time) 연산이다. 반면에 find는 부모 포인터를 따라 트리의 루트로 이동하므로 트리의 높이에 비례하는 시간이 소요된다. 트리는 실제로 세 번째 연산인 union을 통해 구축되므로, 이 프로시저가 트리를 얕게 유지하도록 해야 한다.
두 집합을 병합하는 것은 쉽다: 한 집합의 루트가 다른 집합의 루트를 가리키도록 하면 된다. 하지만 여기에는 선택의 여지가 있다. 집합의 대표자(루트)가 와 일 때, 가 를 가리키게 할 것인가, 아니면 그 반대로 할 것인가? 트리의 높이가 계산 효율성을 저해하는 주요 요인이므로, 더 짧은 트리의 루트가 더 높은 트리의 루트를 가리키도록 하는 것이 좋은 전략이다. 이렇게 하면 병합되는 두 트리의 높이가 같을 때만 전체 높이가 증가한다. 트리의 높이를 명시적으로 계산하는 대신, 루트 노드의 rank 번호를 사용할 것이다. 이것이 이 방식이 union by rank라고 불리는 이유이다.
procedure union ( \(x, y\) )
\(r_{x}=\) find \((x)\)
\(r_{y}=\mathrm{find}(y)\)
if \(r_{x}=r_{y}\) : return
if \(\operatorname{rank}\left(r_{x}\right)>\operatorname{rank}\left(r_{y}\right)\) :
\(\pi\left(r_{y}\right)=r_{x}\)
else:
\(\pi\left(r_{x}\right)=r_{y}\)
if \(\operatorname{rank}\left(r_{x}\right)=\operatorname{rank}\left(r_{y}\right): \operatorname{rank}\left(r_{y}\right)=\operatorname{rank}\left(r_{y}\right)+1\)
예시는 Figure 5.6을 참조하라.
설계상, 노드의 rank는 해당 노드를 루트로 하는 서브트리의 높이와 정확히 일치한다. 이는 예를 들어, 루트 노드를 향해 경로를 따라 이동할 때, 경로를 따라가는 rank 값들이 엄격하게 증가한다는 것을 의미한다.
속성 1 모든 에 대해, 이다.
makeset , makeset , makeset 이후: (A) (B) (C) (D)
union ( ), union ( ), union ( ) 이후:
Figure 5.6 일련의 disjoint-set 연산. 위첨자는 rank를 나타낸다.
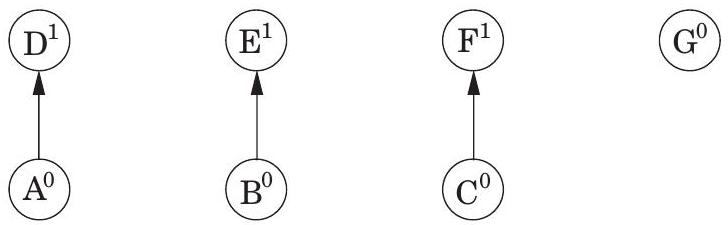
union ( ), union ( ) 이후:

union ( ) 이후:
rank 를 가진 루트 노드는 rank 을 가진 두 트리의 병합으로 생성된다. 귀납법에 의해 (직접 시도해 보라!) 다음이 성립한다.
속성 2 rank 를 가진 모든 루트 노드는 해당 트리에 최소 개의 노드를 가진다. 이는 내부(비루트) 노드에도 적용된다: rank 를 가진 노드는 최소 개의 자손을 가진다. 결국, 모든 내부 노드는 한때 루트였으며, 그 이후로 rank나 자손 집합이 변경되지 않았다. 더욱이, 다른 rank 노드들은 공통 자손을 가질 수 없다. 왜냐하면 속성 1에 의해 모든 요소는 최대 하나의 rank 조상을 가지기 때문이다. 이는 다음을 의미한다.
속성 3 전체 개의 요소가 있다면, rank 를 가진 노드는 최대 개 존재할 수 있다.
이 마지막 관찰은 최대 rank가 이라는 것을 결정적으로 의미한다. 따라서 모든 트리는 높이가 이며, 이는 find 및 union의 실행 시간에 대한 상한이 된다.
Path compression:
지금까지 제시된 데이터 구조를 사용하면 Kruskal 알고리즘의 총 시간 복잡도는 간선을 정렬하는 데 ( 임을 기억하라)가 소요되고, 알고리즘의 나머지 부분을 지배하는 union 및 find 연산에 또 다른 가 소요된다. 따라서 데이터 구조를 더 효율적으로 만들 유인이 거의 없어 보인다.
하지만 간선이 정렬된 상태로 주어진다면 어떨까? 또는 가중치가 작아서 (예: ) 정렬을 선형 시간에 수행할 수 있다면? 이 경우 데이터 구조 부분이 병목 현상이 되며, 연산당 을 넘어 성능을 개선하는 것을 고려하는 것이 유용하다. 결과적으로 개선된 데이터 구조는 다른 많은 응용 분야에서도 유용하다.
하지만 union과 find를 보다 빠르게 수행할 수 있는 방법은 무엇일까? 답은 데이터 구조를 좋은 상태로 유지하기 위해 좀 더 주의를 기울이는 것이다. 모든 주부가 알듯이, 일상적인 유지보수에 약간의 추가 노력을 기울이면 장기적으로 큰 재앙을 막아 큰 보상을 얻을 수 있다. 우리는 union-find 데이터 구조를 위한 특정 유지보수 작업을 염두에 두고 있는데, 이는 트리를 짧게 유지하기 위한 것이다. 각 find 연산 중에 일련의 부모 포인터를 따라 트리의 루트까지 올라갈 때, 이 모든 포인터가 직접 루트를 가리키도록 변경할 것이다 (그림 5.7). 이 경로 압축(path compression) 휴리스틱은 find에 필요한 시간을 약간만 증가시키며 코딩하기 쉽다.
function find(x)
if xf.=\pi(x): \pi(x)=find(\pi(x))
return \pi(x)
이 간단한 변경의 이점은 즉각적이기보다는 장기적이며, 따라서 특정 종류의 분석이 필요하다. 우리는 빈 데이터 구조에서 시작하여 일련의 find 및 union 연산을 살펴보고, 연산당 평균 시간을 결정해야 한다. 이 **상환 비용(amortized cost)**은 이전의 에서 보다 약간 더 많은 수준으로 밝혀졌다.
데이터 구조를 루트 노드로 구성된 "최상위 레벨"과 그 아래의 트리 내부로 생각해보자. 역할 분담이 있다: find 연산(경로 압축 유무와 관계없이)은 트리의 내부만 건드리는 반면, union 연산은 최상위 레벨만 본다. 따라서 경로 압축은 union 연산에 영향을 미치지 않으며 최상위 레벨을 변경하지 않는다.
이제 루트 노드의 랭크는 변경되지 않는다는 것을 알았지만, 비루트 노드는 어떨까? 여기서 핵심은 노드가 일단 루트가 아니게 되면 다시 루트가 되지 않으며,
그림 5.7 경로 압축의 효과: find(I) 다음에 find(K).
그 랭크는 영원히 고정된다는 것이다. 따라서 이 숫자들을 더 이상 트리 높이로 해석할 수 없더라도, 모든 노드의 랭크는 경로 압축에 의해 변경되지 않는다. 특히, (133페이지의) 속성 1-3은 여전히 유효하다.
개의 요소가 있다면, 속성 3에 의해 랭크 값은 0부터 까지 가능하다. 이제 곧 명확해질 이유로 이 범위의 0이 아닌 부분을 신중하게 선택된 특정 구간으로 나누어 보자:
각 그룹은 가 2의 거듭제곱인 형태이다. 그룹의 수는 이며, 이는 을 1 (또는 1 미만)로 만들기 위해 에 적용해야 하는 연속적인 연산의 횟수로 정의된다. 예를 들어, 인데, 이는 이기 때문이다. 실제로는 표시된 구간 중 처음 다섯 개만 사용될 것이다. 더 많은 구간이 필요한 경우는 일 때뿐인데, 이는 다시 말해 결코 일어나지 않는다.
일련의 find 연산에서 일부는 다른 것보다 더 오래 걸릴 수 있다. 우리는 창의적인 회계를 사용하여 전체 실행 시간을 제한할 것이다. 구체적으로, 각 노드에 일정량의 용돈을 주어, 총 지급된 돈이 최대 달러가 되도록 할 것이다. 그런 다음 각 find 연산이 단계와 관련된 노드의 용돈으로 "지불"할 수 있는 추가 시간(시간 단위당 1달러)이 소요됨을 보여줄 것이다. 따라서 개의 find 연산에 대한 전체 시간은 에 최대 를 더한 값이다.
더 자세히 설명하면, 노드는 루트가 아니게 되는 즉시 수당을 받으며, 이때 랭크가 고정된다. 이 랭크가 구간 에 속하면 노드는 달러를 받는다. 속성 3에 의해 랭크가 보다 큰 노드의 수는 다음으로 제한된다.
따라서 이 특정 구간의 노드에 지급되는 총 금액은 최대 달러이며, 개의 구간이 있으므로 모든 노드에 지급되는 총 금액은 이다.
이제 특정 find 연산에 걸리는 시간은 단순히 따라간 포인터의 수이다. 이 노드 체인을 따라 루트까지 올라가는 오름차순 랭크 값을 고려해보자. 체인의 노드 는 두 가지 범주로 나뉜다: 의 랭크가 의 랭크보다 높은 구간에 있거나, 아니면 같은 구간에 있는 경우이다. 첫 번째 유형의 노드는 최대 개이므로 (이유를 알겠는가?), 이들에 대한 작업은 시간이 걸린다. 나머지 노드들, 즉 부모의 랭크가 자신의 랭크와 같은 구간에 있는 노드들은 처리 시간에 대해 용돈에서 1달러를 지불해야 한다.
이것은 각 노드 의 초기 수당이 find 연산 시퀀스에서 모든 지불을 충당하기에 충분할 때만 작동한다. 여기서 중요한 관찰은 다음과 같다: 가 1달러를 지불할 때마다 부모가 더 높은 랭크의 노드로 변경된다. 따라서 의 랭크가 구간 에 속한다면, 부모의 랭크가 더 높은 구간에 속하기 전까지 최대 달러를 지불해야 하며, 그 후에는 다시 지불할 필요가 없다.
5.1.5 Prim's algorithm
최소 신장 트리(minimum spanning tree) 알고리즘에 대한 논의로 돌아가 보자. cut property는 가장 일반적인 용어로 다음의 탐욕적(greedy) 스키마를 따르는 모든 알고리즘이 작동함을 보장한다고 말해준다.
\(X=\{ \}\) (지금까지 선택된 엣지)
repeat until \(|X|=|V|-1\) :
\(X\)가 \(S\)와 \(V-S\) 사이에 엣지를 가지지 않는 집합 \(S \subset V\)를 선택한다.
\(S\)와 \(V-S\) 사이의 최소 가중치 엣지 \(e \in E\)를 선택한다.
\(X=X \cup\{e\}\)
Kruskal's algorithm의 인기 있는 대안은 Prim's algorithm인데, 이 알고리즘에서는 중간 엣지 집합 가 항상 **서브트리(subtree)**를 형성하고, 는 이 트리의 정점 집합으로 선택된다.
각 반복에서 로 정의된 서브트리는 하나의 엣지, 즉 에 있는 정점과 밖에 있는 정점 사이의 가장 가벼운 엣지에 의해 성장한다(Figure 5.8). 우리는 가 가장 작은 비용을 가진 정점 를 포함하도록 성장한다고 동등하게 생각할 수 있다:
Figure 5.8 Prim's algorithm: 엣지 는 트리를 형성하고, 는 그 정점들로 구성된다.
이는 Dijkstra's algorithm을 강력하게 연상시키며, 실제로 의사 코드(Figure 5.9)는 거의 동일하다. 유일한 차이점은 priority queue가 정렬되는 key value에 있다. Prim's algorithm에서 노드의 값은 집합 로부터 들어오는 가장 가벼운 엣지의 가중치인 반면, Dijkstra's algorithm에서는 시작점으로부터 해당 노드까지의 전체 경로 길이이다. 그럼에도 불구하고, 두 알고리즘은 충분히 유사하여 동일한 실행 시간을 가지며, 이는 특정 priority queue 구현에 따라 달라진다.
Figure 5.9는 작은 6개 노드 그래프에서 Prim's algorithm이 작동하는 모습을 보여준다. 최종 MST가 prev 배열에 의해 완전히 지정되는 방식에 주목하라.
5.2 Huffman encoding
MP3 오디오 압축 방식에서, 음향 신호는 세 단계로 인코딩된다.
- 일정한 간격으로 샘플링하여 디지털화되며, 실수 시퀀스 를 생성한다. 예를 들어, 초당 44,100 샘플의 속도로 50분짜리 교향곡은 개의 측정값에 해당한다.
- 각 실수 값 샘플 는 **양자화(quantized)**된다: 유한 집합 의 근처 숫자로 근사된다. 이 집합은 인간의 지각 한계를 활용하도록 신중하게 선택되며, 근사 시퀀스가 인간의 귀로는 와 구별할 수 없도록 하는 것을 목표로 한다.
- 알파벳 에 대한 결과 길이 의 문자열은 이진수로 인코딩된다.
Huffman encoding이 사용되는 것은 마지막 단계이다. 그 역할을 이해하기 위해, 가 1억 3천만이고 알파벳 가 단 네 개의 값, 즉 기호 로 구성된 가상 예시를 살펴보자. 이 긴 문자열을 이진수로 작성하는 가장 경제적인 방법은 무엇일까? 명백한 선택은 기호당 2비트를 사용하는 것이다. 예를 들어, 에 대해 코드워드 00, 에 대해 01, 에 대해 10, 에 대해 11을 사용하면 총 260메가비트가 필요하다. 이보다 더 나은 인코딩이 가능할까?
Figure 5.9 상단: Prim의 최소 신장 트리(minimum spanning tree) 알고리즘. 하단: 노드 에서 시작하는 Prim 알고리즘의 그림. 비용/이전 값 테이블과 최종 MST도 표시되어 있다.
procedure prim (G,w)
Input: A connected undirected graph G = (V,E) with edge
weights we
output: A minimum spanning tree defined by the array prev
for all u\inV:
\operatorname { c o s t } ( u ) = \infty
prev(u) = nil
pick any initial node u
cost(un)=0
H = makequeue (V) (priority queue, using cost-values as keys)
while H is not empty:
v = deletemin (H)
for each {v,z}\inE:
if cost(z)>w(v,z):
cost(z)>w(v,z)
\operatorname { p r e v ( z ) ~ = ~ v }

| Set | ||||||
|---|---|---|---|---|---|---|
| nil | nil | nil | nil | nil | nil | |
| nil | nil | |||||
| nil | ||||||
| nil | ||||||
A randomized algorithm for minimum cut
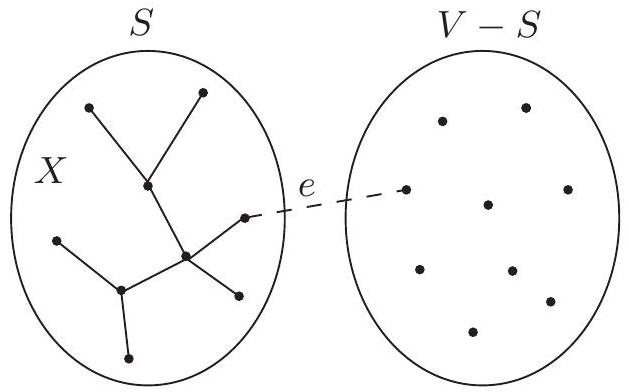
우리는 이미 spanning tree와 cut이 밀접하게 관련되어 있음을 확인했다. 여기에 또 다른 연결점이 있다. Kruskal 알고리즘이 spanning tree에 추가하는 마지막 edge를 제거하면, tree는 두 개의 component로 나뉘고, 이는 그래프에서 cut 를 정의한다. 이 cut에 대해 무엇을 말할 수 있을까? 우리가 다루던 그래프가 unweighted였고, Kruskal 알고리즘이 edge들을 처리하기 위해 무작위로 순서가 지정되었다고 가정해 보자. 여기에 놀라운 사실이 있다: 확률이 최소 일 때, 는 그래프의 minimum cut이다. 여기서 cut 의 크기는 와 사이를 가로지르는 edge의 수이다. 이는 이 과정을 번 반복하고 발견된 가장 작은 cut을 출력하면 높은 확률로 의 minimum cut을 얻을 수 있음을 의미한다. 이는 unweighted minimum cut을 위한 알고리즘이다. 추가적인 튜닝을 통해 David Karger가 발명한 minimum cut 알고리즘을 얻을 수 있으며, 이는 이 중요한 문제에 대해 알려진 가장 빠른 알고리즘이다.
그렇다면 각 iteration에서 발견된 cut이 최소 의 확률로 minimum cut인 이유를 살펴보자. Kruskal 알고리즘의 어떤 단계에서든, vertex 집합 는 연결된 component들로 분할된다. tree에 추가될 수 있는 유일한 edge는 두 endpoint가 서로 다른 component에 있는 edge이다. 각 component에 연결된 edge의 수는 의 minimum cut의 크기인 이상이어야 한다 (이 component를 그래프의 나머지 부분과 분리하는 cut을 고려할 수 있기 때문이다). 따라서 그래프에 개의 component가 있다면, 추가 가능한 edge의 수는 최소 이다 (각 개의 component는 최소 개의 edge가 밖으로 연결되어 있으며, 각 edge의 이중 계산을 보정해야 한다). edge들이 무작위로 순서가 지정되었으므로, 목록에서 다음으로 추가 가능한 edge가 minimum cut에서 나올 확률은 최대 이다. 따라서 최소 의 확률로, 선택은 minimum cut을 손상시키지 않는다. 이제 Kruskal 알고리즘이 마지막 spanning tree edge를 선택할 때까지 minimum cut을 손상시키지 않을 확률은 최소
영감을 얻기 위해, 우리는 특정 시퀀스를 더 자세히 살펴보고 네 가지 기호가 동일하게 풍부하지 않다는 것을 발견한다.
| Symbol | Frequency |
|---|---|
| 70 million | |
| 3 million | |
| 20 million | |
| 37 million |
자주 발생하는 기호 에는 단 1비트만 사용하고, 덜 일반적인 기호에는 3비트 이상이 필요할 수 있는 일종의 가변 길이 인코딩이 있을까?
서로 다른 길이의 codeword를 갖는 것의 위험은 결과 인코딩이 고유하게 해독 가능하지 않을 수 있다는 점이다. 예를 들어, codeword가 인 경우,
| Symbol | Codeword |
|---|---|
| 0 | |
| 100 | |
| 101 | |
| 11 |
그림 5.10 prefix-free 인코딩. 빈도는 대괄호 안에 표시되어 있다.
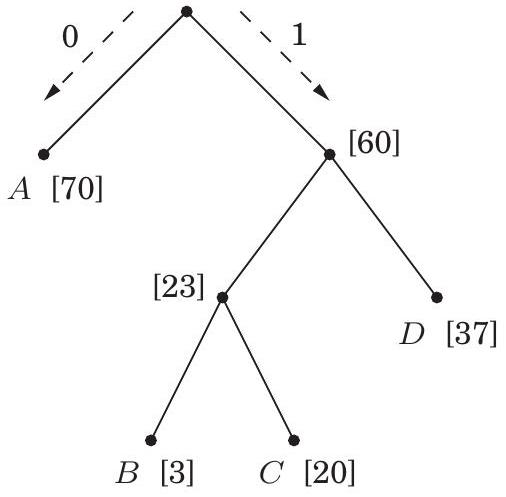
001과 같은 문자열의 디코딩은 모호하다. 우리는 prefix-free 속성을 고수함으로써 이 문제를 피할 것이다: 어떤 codeword도 다른 codeword의 prefix가 될 수 없다.
모든 prefix-free 인코딩은 full binary tree로 표현될 수 있다. 즉, 모든 노드가 자식이 없거나 두 개를 가지는 binary tree이며, 기호는 leaf에 있고, 각 codeword는 root에서 leaf까지의 경로로 생성되며, 왼쪽은 0, 오른쪽은 1로 해석한다 (연습문제 5.29). 그림 5.10은 네 가지 기호 에 대한 이러한 인코딩의 예시를 보여준다. 디코딩은 고유하다: 비트 문자열은 root에서 시작하여 문자열을 왼쪽에서 오른쪽으로 읽어 내려가고, leaf에 도달할 때마다 해당 기호를 출력하고 root로 돌아가서 해독된다. 이는 간단한 방식이며 우리의 예시에서 잘 작동한다. (그림 5.10의 코드에 따라) 이진 문자열의 총 크기는 213메가비트로 줄어들어 17%의 개선을 보인다.
일반적으로, 개의 기호에 대한 빈도 가 주어졌을 때, 최적의 코딩 트리를 어떻게 찾을까? 문제를 정확하게 정의하기 위해, 각 leaf가 기호에 해당하고 인코딩의 전체 길이를 최소화하는 트리를 원한다.
(기호에 필요한 비트 수는 정확히 트리에서의 깊이이다). 이 비용 함수를 작성하는 또 다른 매우 유용한 방법이 있다. leaf에 대한 빈도만 주어졌지만, 모든 internal node의 빈도를 해당 descendant leaf들의 빈도 합으로 정의할 수 있다. 이는 인코딩 또는 디코딩 중에 internal node가 방문되는 횟수이기 때문이다. 인코딩 과정에서, 트리를 내려갈 때마다, root가 아닌 모든 노드를 통과할 때마다 1비트가 출력된다. 따라서 총 비용, 즉 출력되는 총 비트 수는 다음과 같이 표현될 수도 있다:
트리의 비용은 root를 제외한 모든 leaf와 internal node의 빈도 합이다.
비용 함수의 첫 번째 공식은 가장 작은 빈도를 가진 두 기호가 최적 트리의 가장 낮은 internal node의 자식으로서 트리의 가장 아래에 있어야 함을 알려준다 (이 internal node는 트리가 full이므로 두 개의 자식을 가진다). 그렇지 않으면, 이 두 기호를 트리에서 가장 낮은 다른 것과 교환하면 인코딩이 개선될 것이다.
이는 트리를 탐욕적으로 구성하기 시작할 것을 제안한다: 가장 작은 빈도를 가진 두 기호, 예를 들어 와 를 찾아 새로운 노드의 자식으로 만들고, 이 노드는 의 빈도를 갖는다. 표기법을 간단하게 하기 위해, 이들을 과 라고 가정하자. 비용 함수의 두 번째 공식에 따르면, 과 가 형제 leaf인 모든 트리는 와 빈도가 인 개의 leaf를 가진 트리의 비용을 더한 값을 갖는다:
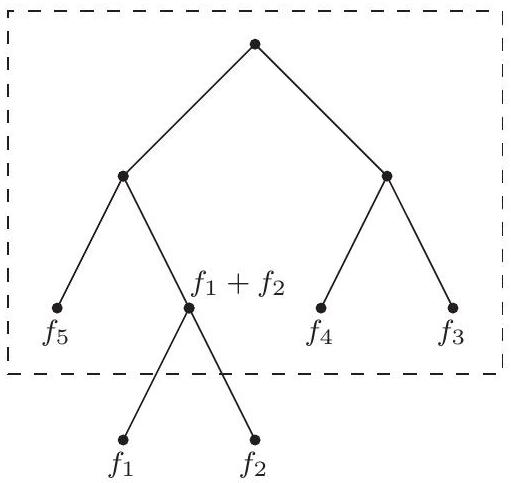
후자의 문제는 우리가 시작한 문제의 더 작은 버전일 뿐이다. 따라서 우리는 빈도 목록에서 과 를 제거하고, 를 삽입한 다음, 반복한다. 결과 알고리즘은 priority queue 연산 (109페이지에 정의된 대로)으로 설명될 수 있으며, binary heap (섹션 4.5.2)을 사용하면 시간이 소요된다.
procedure Huffman(f)
Input: An array f[1 mn] of frequencies
Output: An encoding tree with n leaves
let H be a priority queue of integers, ordered by f
for i=1 to n: insert(H,i)
for k=n+1 to 2n-1:
i=deletemin(H), j= deletemin(H)
create a node numbered k with children i,j
f[k] = f[i] + f[j]
insert(H,k)
우리의 예시로 돌아가서: 그림 5.10의 트리가 최적인지 알 수 있는가?
Entropy
매년 열리는 카운티 경마 대회에 한 번도 서로 경쟁한 적 없는 세 마리의 서러브레드가 출전한다. 당신은 흥미롭게도 이들의 지난 200번의 경주 기록을 연구하여 네 가지 결과(1위, 2위, 3위, 기타)에 대한 확률 분포로 요약했다.
| 결과 | Aurora | Whirlwind | Phantasm |
|---|---|---|---|
| 1위 | 0.15 | 0.30 | 0.20 |
| 2위 | 0.10 | 0.05 | 0.30 |
| 3위 | 0.70 | 0.25 | 0.30 |
| 기타 | 0.05 | 0.40 | 0.20 |
어떤 말이 가장 예측 가능한가? 이 질문에 대한 한 가지 정량적 접근 방식은 **압축성(compressibility)**을 살펴보는 것이다. 각 말의 과거 기록을 200개의 값(1위, 2위, 3위, 기타)으로 이루어진 문자열로 작성한다. 이 경주 기록 문자열을 인코딩하는 데 필요한 총 비트 수는 **허프만 알고리즘(Huffman's algorithm)**을 사용하여 계산할 수 있다. 계산 결과 Aurora는 290비트, Whirlwind는 380비트, Phantasm은 420비트가 필요하다(확인해 보라!). Aurora는 인코딩 길이가 가장 짧으므로 강력한 의미에서 가장 예측 가능하다.
확률 분포의 내재된 예측 불가능성, 즉 **무작위성(randomness)**은 해당 분포에서 추출된 데이터를 압축할 수 있는 정도에 따라 측정될 수 있다.
개의 가능한 결과가 있고, 그 확률이 이라고 가정해 보자. 분포에서 개의 값이 추출되면, 번째 결과는 대략 번 나타날 것이다(이 클 경우). 간단히 말해, 이것이 정확히 관찰된 빈도라고 가정하고, 또한 들이 모두 2의 거듭제곱(즉, 형태)이라고 가정한다. 귀납법(연습문제 5.19)을 통해 시퀀스를 인코딩하는 데 필요한 비트 수가 임을 알 수 있다. 따라서 분포에서 단일 추출을 인코딩하는 데 필요한 평균 비트 수는 다음과 같다.
이것이 분포의 **엔트로피(entropy)**이며, 분포가 포함하는 무작위성의 양을 측정하는 척도이다.
예를 들어, 공정한 동전은 각각 확률이 인 두 가지 결과를 갖는다. 따라서 엔트로피는 다음과 같다.
이는 매우 자연스럽다. 동전 던지기는 1비트의 무작위성을 포함한다. 하지만 동전이 공정하지 않고, 앞면이 나올 확률이 이라면 어떨까? 그러면 엔트로피는 다음과 같다.
편향된 동전은 공정한 동전보다 더 예측 가능하며, 따라서 엔트로피가 더 낮다. 편향이 더 뚜렷해질수록 엔트로피는 0에 가까워진다.
우리는 연습문제 5.18과 5.19에서 이러한 개념들을 더 자세히 탐구한다.
5.3 Horn formulas
인간 수준의 지능을 발휘하려면 컴퓨터는 최소한 어느 정도의 논리적 추론을 수행할 수 있어야 한다. Horn formula는 이를 위한 특정 프레임워크로, 논리적 사실을 표현하고 결론을 도출하는 데 사용된다.
Horn formula의 가장 기본적인 객체는 Boolean 변수로, 참(true) 또는 거짓(false) 값을 갖는다. 예를 들어, 변수 는 다음과 같은 가능성을 나타낼 수 있다.
Literal은 변수 또는 그 부정 ("not ")이다. Horn formula에서 변수에 대한 지식은 두 가지 종류의 clause로 표현된다.
-
Implication: 좌변은 여러 개의 positive literal의 논리곱(AND)이고, 우변은 단일 positive literal이다. 이는 "좌변의 조건이 충족되면 우변의 조건도 참이어야 한다"는 형태의 진술을 표현한다. 예를 들어,
는 "대령이 오후 8시에 잠들어 있었고 살인이 오후 8시에 일어났다면 집사는 무죄이다"를 의미할 수 있다. 퇴화된 형태의 implication은 단일 ""로, 단순히 가 참이라는 의미이다: "살인은 분명히 부엌에서 일어났다."
-
Pure negative clause: 여러 개의 negative literal의 논리합(OR)으로 구성된다. 예를 들어,
("그들 모두가 무죄일 수는 없다").
이 두 가지 유형의 clause 집합이 주어졌을 때, 목표는 일관된 설명, 즉 모든 clause를 만족시키는 변수에 대한 참/거짓 값 할당이 있는지 여부를 결정하는 것이다. 이를 satisfying assignment라고도 한다.
두 가지 종류의 clause는 서로 다른 방향으로 작용한다. implication은 일부 변수를 참으로 설정하도록 지시하는 반면, negative clause는 변수를 거짓으로 만들도록 권장한다. Horn formula를 해결하기 위한 우리의 전략은 다음과 같다: 모든 변수를 거짓으로 시작한다. 그런 다음, 일부 변수를 하나씩 참으로 설정하지만, 매우 마지못해, 그리고 implication이 위반될 경우에만 그렇게 한다. 이 단계가 완료되고 모든 implication이 만족되면, 그제서야 negative clause로 넘어가 모든 negative clause가 만족되는지 확인한다.
다시 말해, Horn clause에 대한 우리의 알고리즘은 다음의 greedy scheme이다 (어쩌면 "stingy"가 더 적절한 표현일 것이다):
Input: a Horn formula
Output: a satisfying assignment, if one exists
set all variables to false
while there is an implication that is not satisfied:
set the right-hand variable of the implication to true
if all pure negative clauses are satisfied:
return the assignment
else: return "formula is not satisfiable"
예를 들어, formula가 다음과 같다고 가정해 보자.
우리는 모든 것을 거짓으로 시작한 다음, 단일 implication 때문에 가 참이어야 한다는 것을 알아차린다. 그런 다음, 때문에 도 참이어야 한다는 것을 알게 된다. 이런 식으로 계속 진행된다.
이 알고리즘이 올바른 이유를 이해하려면, 만약 알고리즘이 assignment를 반환한다면, 이 assignment는 implication과 negative clause를 모두 만족시키므로, 입력 Horn formula의 satisfying truth assignment가 된다는 점에 주목해야 한다. 따라서 우리는 알고리즘이 satisfying assignment를 찾지 못했을 때, 실제로 satisfying assignment가 없다는 것을 스스로 납득시키기만 하면 된다. 이는 우리의 "stingy" 규칙이 다음 invariant를 유지하기 때문이다:
특정 변수 집합이 참으로 설정되면, 이 변수들은 어떤 satisfying assignment에서도 참이어야 한다.
따라서 while 루프 후에 발견된 truth assignment가 negative clause를 만족시키지 못한다면, satisfying truth assignment는 존재할 수 없다.
Horn formula는 간단한 논리적 표현식을 사용하여 출력의 원하는 속성을 지정함으로써 프로그래밍하는 언어인 Prolog("programming by logic")의 핵심에 있다. Prolog interpreter의 핵심은 우리의 greedy satisfiability 알고리즘이다. 편리하게도, 이 알고리즘은 formula의 길이에 비례하는 선형 시간 안에 구현될 수 있다; 어떻게 가능한지 아는가 (Exercise 5.33)?
5.4 Set cover
그림 5.11의 점들은 마을들의 집합을 나타낸다. 이 카운티는 계획 초기 단계에 있으며 학교를 어디에 지을지 결정하고 있다. 제약 조건은 두 가지뿐이다: 각 학교는 마을 안에 있어야 하고, 누구도 학교에 가기 위해 30마일 이상을 이동할 필요가 없어야 한다. 필요한 최소 학교 수는 몇 개인가?
이는 전형적인 **집합 커버 문제(set cover problem)**이다. 각 마을 에 대해, 를 로부터 30마일 이내에 있는 마을들의 집합이라고 하자. 에 있는 학교는 본질적으로 이 다른 마을들을 "커버"할 것이다.
그림 5.11 (a) 11개의 마을. (b) 서로 30마일 이내에 있는 마을들.
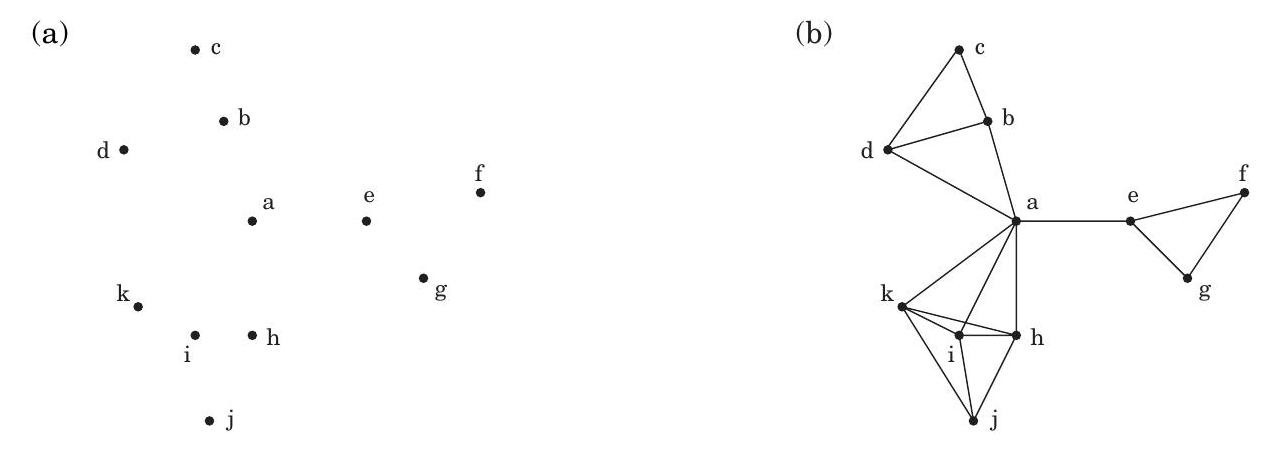
그렇다면, 카운티의 모든 마을을 커버하기 위해 몇 개의 집합 를 선택해야 하는가?
Set Cover
입력: 요소 집합 ; 집합 출력: 합집합이 가 되는 의 선택 비용: 선택된 집합의 수. (예시에서 의 요소는 마을이다.) 이 문제는 즉시 탐욕적(greedy) 해법으로 이어진다:
의 모든 요소가 덮일 때까지 반복: 가장 많은 수의 덮이지 않은 요소를 가진 집합 를 선택한다. 이것은 매우 자연스럽고 직관적이다. 이전 예시에서 이 방법이 어떻게 작동하는지 살펴보자: 이 방법은 가장 많은 다른 마을을 덮기 때문에 먼저 마을 에 학교를 배치할 것이다. 그 후, 세 개의 학교(, 그리고 또는 중 하나)를 더 선택하여 총 네 개의 학교를 배치할 것이다. 그러나 에 단 세 개의 학교만으로도 해결책이 존재한다. 탐욕적 방식은 최적이 아니다!
하지만 다행히도 최적에서 그리 멀지 않다. 주장: 가 개의 요소를 포함하고 최적의 커버가 개의 집합으로 구성된다고 가정하자. 그러면 탐욕적 알고리즘은 최대 개의 집합을 사용할 것이다.
번의 탐욕적 알고리즘 반복 후 아직 덮이지 않은 요소의 수를 라고 하자(). 이 남아있는 요소들은 최적의 개 집합에 의해 덮이므로, 그 중 적어도 개를 포함하는 집합이 반드시 존재해야 한다. 따라서 탐욕적 전략은 다음을 보장한다:
이를 반복적으로 적용하면 가 된다. 더 편리한 상한은 유용한 부등식에서 얻을 수 있다:
이는 그림으로 가장 쉽게 증명된다:
따라서
그러므로 일 때, 는 보다 엄격히 작으며, 이는 덮어야 할 요소가 남아있지 않음을 의미한다.
탐욕적 알고리즘의 해와 최적 해 사이의 비율은 입력마다 다르지만 항상 보다 작다. 그리고 이 비율이 에 매우 가까운 특정 입력도 존재한다(연습문제 5.34). 우리는 이 최대 비율을 **탐욕적 알고리즘의 근사 계수(approximation factor)**라고 부른다. 개선의 여지가 많아 보이지만, 사실 그러한 기대는 정당하지 않다: 특정 널리 받아들여지는 복잡성 가정(8장에서 더 명확해질 것이다) 하에서는 더 작은 근사 계수를 가진 다항 시간 알고리즘이 존재하지 않는다는 것이 증명되었다.
Exercises
5.1. 다음 그래프를 고려하시오.
 (a) 이 그래프의 최소 신장 트리(minimum spanning tree) 비용은 얼마인가?
(b) 이 그래프는 몇 개의 최소 신장 트리를 가지는가?
(c) 이 그래프에 Kruskal의 알고리즘을 실행한다고 가정하자. 간선들은 어떤 순서로 MST에 추가되는가? 이 시퀀스의 각 간선에 대해, 추가를 정당화하는 cut을 제시하시오.
5.2. 다음 그래프의 최소 신장 트리를 찾고자 한다고 가정하자.
(a) 이 그래프의 최소 신장 트리(minimum spanning tree) 비용은 얼마인가?
(b) 이 그래프는 몇 개의 최소 신장 트리를 가지는가?
(c) 이 그래프에 Kruskal의 알고리즘을 실행한다고 가정하자. 간선들은 어떤 순서로 MST에 추가되는가? 이 시퀀스의 각 간선에 대해, 추가를 정당화하는 cut을 제시하시오.
5.2. 다음 그래프의 최소 신장 트리를 찾고자 한다고 가정하자.
 (a) Prim의 알고리즘을 실행하시오. 노드를 선택할 때마다 항상 알파벳 순서(예: 노드 부터 시작)를 사용하시오. 비용 배열의 중간 값을 보여주는 표를 그리시오.
(b) 동일한 그래프에 Kruskal의 알고리즘을 실행하시오. path compression이 사용된다고 가정하고, 모든 중간 단계(directed tree의 구조 포함)에서 disjoint-sets data structure가 어떻게 보이는지 보여주시오.
5.3. 다음 작업을 위한 선형 시간 알고리즘을 설계하시오.
(a) Prim의 알고리즘을 실행하시오. 노드를 선택할 때마다 항상 알파벳 순서(예: 노드 부터 시작)를 사용하시오. 비용 배열의 중간 값을 보여주는 표를 그리시오.
(b) 동일한 그래프에 Kruskal의 알고리즘을 실행하시오. path compression이 사용된다고 가정하고, 모든 중간 단계(directed tree의 구조 포함)에서 disjoint-sets data structure가 어떻게 보이는지 보여주시오.
5.3. 다음 작업을 위한 선형 시간 알고리즘을 설계하시오.
입력: 연결된 무방향 그래프 . 질문: 에서 간선을 제거해도 가 여전히 연결된 상태를 유지하는 간선이 있는가? 알고리즘의 실행 시간을 로 줄일 수 있는가? 5.4. 개의 정점을 가진 무방향 그래프가 개의 연결된 컴포넌트를 가진다면, 적어도 개의 간선을 가진다는 것을 보이시오. 5.5. 음이 아닌 간선 가중치 를 가진 무방향 그래프 를 고려하시오. 의 최소 신장 트리를 계산했고, 특정 노드 에서 모든 노드까지의 최단 경로도 계산했다고 가정하자. 이제 각 간선 가중치가 1씩 증가하여 새로운 가중치가 이 되었다고 가정하자. (a) 최소 신장 트리가 변하는가? 변하는 예시를 제시하거나 변할 수 없음을 증명하시오. (b) 최단 경로가 변하는가? 변하는 예시를 제시하거나 변할 수 없음을 증명하시오. 5.6. 가 무방향 그래프라고 하자. 모든 간선 가중치가 서로 다르다면, 유일한 최소 신장 트리를 가진다는 것을 증명하시오. 5.7. 그래프의 최대 신장 트리(maximum spanning tree), 즉 총 가중치가 가장 큰 신장 트리를 찾는 방법을 보이시오. 5.8. 양수이고 서로 다른 모든 간선 가중치를 가진 연결된 가중치 그래프 와 구별되는 정점 가 주어졌다고 가정하자. 에서 시작하는 최단 경로 트리와 의 최소 신장 트리가 어떤 간선도 공유하지 않는 것이 가능한가? 가능하다면 예시를 제시하시오. 불가능하다면 이유를 제시하시오. 5.9. 다음 진술들은 옳을 수도 있고 옳지 않을 수도 있다. 각 경우에 대해, 옳다면 증명하고(correct), 옳지 않다면 반례를 제시하시오(incorrect). 항상 그래프 가 무방향이고 연결되어 있다고 가정하시오. 간선 가중치가 명시적으로 다르다고 언급되지 않는 한, 다르다고 가정하지 마시오. (a) 그래프 가 개 이상의 간선을 가지고 있고, 유일하게 가장 무거운 간선이 있다면, 이 간선은 최소 신장 트리의 일부가 될 수 없다. (b) 가 유일하게 가장 무거운 간선 를 가진 사이클을 포함한다면, 는 어떤 MST의 일부도 될 수 없다. (c) 가 에서 최소 가중치를 가진 간선이라면, 는 어떤 MST의 일부여야 한다. (d) 그래프에서 가장 가벼운 간선이 유일하다면, 그것은 모든 MST의 일부여야 한다. (e) 가 의 어떤 MST의 일부라면, 그것은 의 어떤 cut을 가로지르는 가장 가벼운 간선이어야 한다. (f) 가 유일하게 가장 가벼운 간선 를 가진 사이클을 포함한다면, 는 모든 MST의 일부여야 한다. (g) Dijkstra의 알고리즘으로 계산된 최단 경로 트리는 반드시 MST이다. (h) 두 노드 사이의 최단 경로는 반드시 어떤 MST의 일부이다. (i) Prim의 알고리즘은 음수 간선이 있을 때도 올바르게 작동한다. (j) (어떤 에 대해, -경로를 모든 간선이 가중치 을 가지는 경로로 정의한다.) 가 노드 에서 까지의 -경로를 포함한다면, 의 모든 MST도 노드 에서 노드 까지의 -경로를 포함해야 한다. 5.10. 가 그래프 의 MST라고 하자. 의 연결된 부분 그래프 가 주어졌을 때, 가 의 어떤 MST에 포함된다는 것을 보이시오. 5.11. 단일 집합 에서 시작하여 다음 연산 시퀀스 후의 disjoint-sets data structure의 상태를 제시하시오. path compression을 사용하시오. 동점인 경우, 항상 더 작은 번호의 루트가 더 큰 번호의 루트를 가리키도록 하시오.
union(1,2), union(3,4), union(5,6), union(7,8), union(1,4),
union(6, 7), union(4, 5), find(1)
5.12. union-by-rank를 사용하지만 path compression을 사용하지 않는 disjoint-sets data structure를 구현한다고 가정하자. 개의 요소에 대해 시간이 걸리는 개의 union 및 find 연산 시퀀스를 제시하시오. 5.13. 긴 문자열이 네 가지 문자 로 구성되어 있으며, 각각 의 빈도로 나타난다. 이 네 문자의 Huffman encoding은 무엇인가? 5.14. 기호 가 각각 의 빈도로 나타난다고 가정하자. (a) 이 알파벳의 Huffman encoding은 무엇인가? (b) 이 인코딩이 주어진 빈도로 개의 문자로 구성된 파일에 적용된다면, 인코딩된 파일의 길이는 비트 단위로 얼마인가? 5.15. Huffman의 알고리즘을 사용하여 빈도 를 가진 알파벳 의 인코딩을 얻는다. 다음 각 경우에 대해, 지정된 코드를 생성할 빈도()의 예시를 제시하거나, 코드를 얻을 수 없는 이유를 설명하시오(빈도와 관계없이). (a) 코드: (b) 코드: (c) 코드: 5.16. Huffman encoding scheme의 다음 두 가지 속성을 증명하시오. (a) 어떤 문자가 보다 큰 빈도로 나타나면, 길이가 1인 코드워드가 보장된다. (b) 모든 문자가 보다 작은 빈도로 나타나면, 길이가 1인 코드워드가 없다는 것이 보장된다. 5.17. 빈도 을 가진 개의 기호에 대한 Huffman encoding에서 코드워드가 가질 수 있는 가장 긴 길이는 얼마인가? 이 경우를 생성할 빈도 집합의 예시를 제시하시오. 5.18. 다음 표는 특정 코퍼스에서 영어 알파벳(단어 구분을 위한 공백 포함)의 빈도를 제공한다.
| blank | r | y | |||
|---|---|---|---|---|---|
| e | d | p | |||
| t | l | b | |||
| a | c | v | |||
| o | u | k | |||
| i | m | j | |||
| n | w | x | |||
| s | f | q | |||
| h | g | z |
(a) 이 알파벳의 최적 Huffman encoding은 무엇인가? (b) 글자당 예상 비트 수는 얼마인가? (c) 이제 이 빈도의 엔트로피를 계산한다고 가정하자.
(143페이지의 상자를 참조하시오). 이 값이 위에서 얻은 답보다 크다고 예상하는가, 작다고 예상하는가? 설명하시오. (d) 이것이 영어 텍스트를 압축할 수 있는 한계라고 생각하는가? 더 나은 압축 스키마가 고려해야 할, 글자와 그 빈도 외의 영어 언어의 특징은 무엇인가? 5.19. 엔트로피. 확률 을 가진 가지 가능한 결과에 대한 분포를 고려하시오. (a) 이 문제의 이 부분에 대해서만, 각 가 2의 거듭제곱(즉, 형태)이라고 가정하자. 분포에서 개의 샘플로 구성된 긴 시퀀스가 추출되고, 모든 에 대해 번째 결과가 시퀀스에서 정확히 번 발생한다고 가정하자. 이 시퀀스에 Huffman encoding이 적용되면, 결과 인코딩의 길이가 다음과 같음을 보이시오.
(b) 이제 임의의 분포를 고려하시오. 즉, 확률 가 2의 거듭제곱으로 제한되지 않는다. 분포의 무작위성 양을 측정하는 가장 일반적으로 사용되는 척도는 엔트로피이다.
어떤 분포(가지 결과에 대한)에서 엔트로피가 가장 큰가? 가장 작은가? 5.20. 트리를 입력으로 받아 perfect matching(각 노드를 정확히 한 번씩 접하는 간선 집합)을 가지는지 여부를 결정하는 선형 시간 알고리즘을 제시하시오. 5.21. 무방향 그래프 의 feedback edge set은 그래프의 모든 사이클과 교차하는 간선 집합 이다. 따라서 간선 를 제거하면 그래프는 비순환(acyclic)이 된다.
다음 문제에 대한 효율적인 알고리즘을 제시하시오.
입력: 양수 간선 가중치 를 가진 무방향 그래프 출력: 최소 총 가중치 를 가진 feedback edge set 5.22. 이 문제에서는 최소 신장 트리를 찾는 새로운 알고리즘을 개발할 것이다. 이 알고리즘은 다음 속성을 기반으로 한다.
그래프에서 임의의 사이클을 선택하고, 그 사이클에서 가장 무거운 간선을 라고 하자. 그러면 를 포함하지 않는 최소 신장 트리가 존재한다. (a) 이 속성을 신중하게 증명하시오. (b) 다음은 새로운 MST 알고리즘이다. 입력은 간선 가중치 를 가진 무방향 그래프 (인접 리스트 형식)이다.
간선을 가중치에 따라 정렬한다.
각 간선 e \in E에 대해, we의 내림차순으로:
만약 e가 G의 사이클의 일부라면:
G = G - e (즉, G에서 e를 제거한다)
G를 반환한다.
이 알고리즘이 올바르다는 것을 증명하시오. (c) 각 반복에서 알고리즘은 특정 간선 를 포함하는 사이클이 있는지 확인해야 한다. 이 작업을 위한 선형 시간 알고리즘을 제시하고 그 정확성을 정당화하시오. (d) 이 알고리즘이 에 대해 걸리는 전체 시간은 얼마인가? 5.23. 양수 간선 가중치를 가진 그래프 와 이 가중치에 대한 최소 신장 트리 가 주어졌다고 가정하자. 와 는 인접 리스트로 주어진다고 가정할 수 있다. 이제 특정 간선 의 가중치가 에서 새로운 값 로 수정되었다고 가정하자. 전체 트리를 처음부터 다시 계산하지 않고 이 변경 사항을 반영하도록 최소 신장 트리 를 빠르게 업데이트하고자 한다. 네 가지 경우가 있다. 각 경우에 대해 트리를 업데이트하는 선형 시간 알고리즘을 제시하시오. (a) 이고 . (b) 이고 . (c) 이고 . (d) 이고 . 5.24. 때로는 특정 특별한 속성을 가진 가벼운 신장 트리를 원한다. 다음은 그 예시이다.
입력: 무방향 그래프 ; 간선 가중치 ; 정점의 부분 집합 출력: 의 노드들이 leaf인 가장 가벼운 신장 트리 (이 트리에는 다른 leaf도 있을 수 있다). (답은 반드시 최소 신장 트리는 아니다.) 시간으로 실행되는 이 문제에 대한 알고리즘을 제시하시오. (힌트: 최적 해에서 노드 를 제거하면 무엇이 남는가?) 5.25. 길이가 지정되지 않은 이진 카운터는 두 가지 연산을 지원한다: increment(값을 1 증가시킴) 및 reset(값을 0으로 재설정함). 초기 값이 0인 카운터에서 시작하여 개의 increment 및 reset 연산 시퀀스가 시간이 걸린다는 것을 보이시오. 즉, 연산당 **상환 시간(amortized time)**은 이다. 5.26. 다음은 자동 프로그램 분석에서 발생하는 문제이다. 변수 집합 에 대해, " " 형태의 등식 제약 조건과 " " 형태의 부등식 제약 조건이 주어진다. 이 모든 제약 조건을 만족시키는 것이 가능한가? 예를 들어, 다음 제약 조건은
만족될 수 없다. 개의 변수에 대한 개의 제약 조건을 입력으로 받아 제약 조건이 만족될 수 있는지 여부를 결정하는 효율적인 알고리즘을 제시하시오. 5.27. 주어진 차수 시퀀스를 가진 그래프. 개의 양의 정수 목록이 주어졌을 때, 노드의 차수가 정확히 인 무방향 그래프 가 존재하는지 효율적으로 결정하고자 한다. 즉, 이라면, 의 차수는 정확히 여야 한다. 우리는 ()을 의 **차수 시퀀스(degree sequence)**라고 부른다. 이 그래프 는 self-loop(양 끝점이 같은 노드인 간선) 또는 같은 노드 쌍 사이의 multiple edges를 포함해서는 안 된다. (a) 모든 이고 가 짝수이지만, 차수 시퀀스 ()를 가진 그래프가 존재하지 않는 의 예시를 제시하시오. (b) 이고 차수 시퀀스 를 가진 그래프 가 존재한다고 가정하자. 우리는 이 차수 시퀀스를 가지면서 추가적으로 의 이웃이 인 그래프가 존재해야 함을 보이고자 한다. 아이디어는 를 원하는 추가 속성을 가진 그래프로 점진적으로 변환하는 것이다. i. 에서 의 이웃이 이 아니라고 가정하자. 이고 인 및 가 존재함을 보이시오. ii. 와 동일한 차수 시퀀스를 가지며 () 인 새로운 그래프 를 얻기 위해 에 적용할 변경 사항을 지정하시오. iii. 이제 주어진 차수 시퀀스를 가지지만 이 이웃 을 가지는 그래프가 존재해야 함을 보이시오. (c) (b) 부분의 결과를 사용하여, 입력 (반드시 정렬되지 않아도 됨)에 대해 이 차수 시퀀스를 가진 그래프가 존재하는지 여부를 결정하는 알고리즘을 설명하시오. 알고리즘은 에 대해 다항 시간으로 실행되어야 한다. 5.28. 앨리스는 파티를 열고 누구를 초대할지 결정하고 있다. 그녀는 명의 사람 중에서 선택해야 하며, 이 사람들 중 어떤 쌍이 서로 아는지 목록을 작성했다. 그녀는 두 가지 제약 조건 하에 가능한 한 많은 사람을 선택하고자 한다: 파티에서 각 사람은 적어도 다섯 명의 아는 사람과 다섯 명의 모르는 사람을 가져야 한다. 명의 사람 목록과 서로 아는 쌍의 목록을 입력으로 받아 파티 초대자의 최적 선택을 출력하는 효율적인 알고리즘을 제시하시오. 에 대한 실행 시간을 제시하시오. 5.29. 유한 알파벳 의 prefix-free encoding은 의 각 기호에 이진 코드워드를 할당하며, 어떤 코드워드도 다른 코드워드의 접두사가 되지 않는다. prefix-free encoding은 일부 키워드를 축약하여 다른 prefix-free encoding(동일한 기호의)에 도달할 수 없을 때 minimal이다. 예를 들어, 인코딩 은 코드워드 101을 1로 축약해도 prefix-free 속성을 유지하므로 minimal이 아니다. minimal prefix-free encoding이 full binary tree로 표현될 수 있음을 보이시오. 이 트리에서 각 leaf는 의 고유한 요소에 해당하며, 해당 코드워드는 루트에서 해당 leaf까지의 경로(왼쪽 가지를 0, 오른쪽 가지를 1로 해석)에 의해 생성된다. 5.30. 삼진 Huffman. Trimedia Disks Inc.는 "삼진" 하드 디스크를 개발했다. 이제 디스크의 각 셀은 0, 1, 또는 2의 값을 저장할 수 있다(0 또는 1만 저장하는 대신). 이 새로운 기술을 활용하기 위해, 알려진 빈도 로 나타나는 크기 의 알파벳에서 문자 시퀀스를 압축하기 위한 수정된 Huffman 알고리즘을 제공하시오. 알고리즘은 각 문자를 0, 1, 2 값에 대한 가변 길이 코드워드로 인코딩해야 하며, 어떤 코드워드도 다른 코드워드의 접두사가 되지 않도록 하고 가능한 최대 압축을 얻어야 한다. 알고리즘이 올바르다는 것을 증명하시오. 5.31. Huffman의 알고리즘의 기본 직관은 빈번한 블록은 짧은 인코딩을 가져야 하고 빈번하지 않은 블록은 긴 인코딩을 가져야 한다는 것이다. 이는 영어에서도 작동하는데, I, you, is, and, to, from 등과 같은 일반적인 단어는 짧고, velociraptor와 같이 거의 사용되지 않는 단어는 더 길다. 그러나 fire!, help!, run!과 같은 단어는 빈번해서가 아니라, 아마도 사용되는 상황에서 시간이 소중하기 때문에 짧다.
이론적으로 설명하자면, 개의 다른 단어로 구성된 파일이 있고, 빈도는 이라고 가정하자. 또한 번째 단어에 대해 인코딩의 비트당 비용이 라고 가정하자. 따라서 번째 단어가 길이 의 코드워드를 가지는 prefix-free code를 찾으면, 인코딩의 총 비용은 가 된다. 최소 총 비용의 prefix-free encoding을 찾는 방법을 보이시오. 5.32. 서버에 명의 고객이 서비스를 기다리고 있다. 각 고객에게 필요한 서비스 시간은 미리 알려져 있다: 고객 에게는 분이다. 따라서 예를 들어, 고객들이 가 증가하는 순서로 서비스된다면, 번째 고객은 분 동안 기다려야 한다. 우리는 총 대기 시간을 최소화하고자 한다.
고객을 처리하는 최적의 순서를 계산하는 효율적인 알고리즘을 제시하시오. 5.33. Horn formula satisfiability를 위한 stingy algorithm(섹션 5.3)을 공식의 길이(리터럴의 발생 횟수)에 비례하는 시간으로 구현하는 방법을 보이시오. 5.34. 2의 거듭제곱인 임의의 정수 에 대해, 다음 속성을 가진 set cover problem(섹션 5.4)의 인스턴스가 존재함을 보이시오. i. 기본 집합에 개의 요소가 있다. ii. 최적 커버는 단 두 개의 집합만 사용한다. iii. **탐욕 알고리즘(greedy algorithm)**은 적어도 개의 집합을 선택한다.
따라서 이 장에서 도출한 근사 비율은 tight하다. 5.35. 개의 노드를 가진 비가중치 그래프는 최대 개의 서로 다른 minimum cuts를 가진다는 것을 보이시오.
Chapter 6
Dynamic programming
이전 장들에서 우리는 분할 정복(divide-and-conquer), 그래프 탐색(graph exploration), **탐욕적 선택(greedy choice)**과 같이 다양한 중요한 계산 task에 대한 명확한 알고리즘을 도출하는 몇 가지 우아한 설계 원칙들을 살펴보았다. 이러한 도구들의 단점은 매우 특정한 유형의 문제에만 사용될 수 있다는 점이다. 이제 우리는 알고리즘 기술의 두 가지 강력한 도구인 **동적 프로그래밍(dynamic programming)**과 **선형 프로그래밍(linear programming)**으로 넘어갈 것이다. 이들은 보다 전문화된 방법들이 실패할 때 호출될 수 있는 매우 광범위한 적용 가능성을 가진 기술들이다. 예상할 수 있듯이, 이러한 일반성은 종종 효율성 측면에서 비용을 수반한다.
6.1 Shortest paths in dags, revisited
최단 경로에 대한 연구(4장)를 마무리하면서, 우리는 **방향 비순환 그래프(dag)**에서 이 문제가 특히 쉽다는 것을 관찰했다. 이 경우가 동적 프로그래밍의 핵심에 있기 때문에 다시 한번 살펴보자.
dag의 특별한 특징은 노드를 선형화할 수 있다는 것이다. 즉, 모든 edge가 왼쪽에서 오른쪽으로 가도록 노드를 한 줄로 배열할 수 있다(그림 6.1). 이것이 최단 경로에 어떻게 도움이 되는지 이해하기 위해, 노드 에서 다른 노드까지의 거리를 알아내고 싶다고 가정해 보자. 구체적으로 노드 에 초점을 맞추자. 에 도달하는 유일한 방법은 선행 노드인 또는 를 통하는 것이다. 따라서 까지의 최단 경로를 찾으려면 이 두 경로를 비교하기만 하면 된다:
모든 노드에 대해 유사한 관계를 작성할 수 있다. 그림 6.1의 왼쪽에서 오른쪽 순서로 이러한 dist 값을 계산하면, 노드 에 도달할 때쯤에는 dist()를 계산하는 데 필요한 모든 정보를 이미 가지고 있다고 항상 확신할 수 있다. 따라서 우리는 단일 pass로 모든 거리를 계산할 수 있다:
initialize all dist(.) values to \(\infty\)
dist \((s)=0\)
for each \(v \in V \backslash\{s\}\), in linearized order:
dist \((v)=\min _{(u, v) \in E}\{\) dist \((u)+l(u, v)\}\)
이 알고리즘이 ist 와 같은 하위 문제(subproblems) 집합을 해결하고 있다는 점에 주목하자. 우리는 가장 작은 하위 문제인 dist(s)부터 시작하는데, 그 답이 0이라는 것을 즉시 알기 때문이다. 그런 다음 점진적으로 "더 큰" 하위 문제, 즉 선형화에서 점점 더 멀리 떨어진 정점까지의 거리를 진행한다. 여기서 하위 문제는 그것에 도달하기 전에 많은 다른 하위 문제를 해결해야 한다면 큰 것으로 간주한다.
이것은 매우 일반적인 기술이다. 각 노드에서 우리는 노드의 선행 노드 값에 대한 어떤 함수를 계산한다. 우리의 특정 함수는 합의 최솟값이지만, 최댓값으로 만들 수도 있으며, 이 경우 dag에서 최장 경로를 얻게 된다. 또는 괄호 안에 합 대신 곱을 사용할 수도 있으며, 이 경우 edge 길이의 곱이 가장 작은 경로를 계산하게 된다.
동적 프로그래밍은 문제 해결을 위해 하위 문제 집합을 식별하고, 가장 작은 것부터 하나씩 해결하며, 작은 문제의 답을 사용하여 더 큰 문제를 해결하는 데 도움을 주고, 결국 모든 문제를 해결하는 매우 강력한 알고리즘 패러다임이다. 동적 프로그래밍에서는 dag가 주어지지 않는다. dag는 암시적이다. 그 노드는 우리가 정의하는 하위 문제들이고, 그 edge는 하위 문제들 간의 의존성이다. 만약 하위 문제 를 해결하기 위해 하위 문제 의 답이 필요하다면, 에서 로의 (개념적인) edge가 존재한다. 이 경우 는 보다 작은 하위 문제로 간주되며, 항상 명백한 의미에서 더 작을 것이다.
하지만 이제 예시를 볼 때이다.
그림 6.1 dag와 그 선형화(위상 정렬).
6.2 Longest increasing subsequences
가장 긴 증가 부분 수열(longest increasing subsequence) 문제에서 입력은 숫자 시퀀스 이다. 부분 수열(subsequence)은 이 숫자들 중 순서대로 취한 모든 부분 집합으로, 형태의 이다. 증가 부분 수열(increasing subsequence)은 숫자가 엄격하게 커지는 부분 수열이다. 목표는 가장 긴 증가 부분 수열을 찾는 것이다. 예를 들어, 의 가장 긴 증가 부분 수열은 이다:
그림 6.2 증가 부분 수열의 dag.
이 예시에서 화살표는 최적 해의 연속적인 요소들 간의 전이(transition)를 나타낸다. 더 일반적으로, 해 공간을 더 잘 이해하기 위해 모든 허용 가능한 전이의 그래프를 만들어 보자: 각 요소 에 대해 노드 를 설정하고, 와 가 증가 부분 수열에서 연속적인 요소가 될 수 있을 때마다, 즉 이고 일 때마다 방향성 에지 를 추가한다 (그림 6.2).
(1) 이 그래프 는 모든 에지 가 를 가지므로 dag이며, (2) 증가 부분 수열과 이 dag의 경로 사이에 일대일 대응이 있다는 점에 주목하자. 따라서 우리의 목표는 단순히 dag에서 가장 긴 경로를 찾는 것이다!
다음은 알고리즘이다:
for \(j=1,2, \ldots, n\) :
\(L(j)=1+\max \{L(i):(i, j) \in E\}\)
return \(\max _{j} L(j)\)
는 에서 끝나는 가장 긴 경로(가장 긴 증가 부분 수열)의 길이이다 (엄밀히 말하면 에지가 아닌 경로상의 노드를 세어야 하므로 1을 더한다). 최단 경로에서와 동일한 방식으로 추론하면, 노드 로 가는 모든 경로는 그 선행 노드 중 하나를 통과해야 하므로, 는 이 선행 노드들의 최대 값에 1을 더한 값이다. 만약 로 들어오는 에지가 없다면, 빈 집합에 대한 최댓값인 0을 취한다. 그리고 최종 답은 가장 큰 인데, 이는 어떤 끝 위치도 허용되기 때문이다.
이것은 **동적 프로그래밍(dynamic programming)**이다. 원래 문제를 해결하기 위해, 우리는 다음과 같은 핵심 속성을 가진 하위 문제들의 집합 을 정의했다. 이 속성 덕분에 하위 문제들을 한 번의 통과로 해결할 수 있다: (*) 하위 문제들에 대한 순서가 존재하며, "더 작은" 하위 문제들, 즉 순서상 먼저 나타나는 하위 문제들의 답이 주어졌을 때 하위 문제를 해결하는 방법을 보여주는 관계가 존재한다.
우리의 경우, 각 하위 문제는 다음 관계를 사용하여 해결된다:
이 표현식은 더 작은 하위 문제들만을 포함한다. 이 단계는 얼마나 걸리는가? 의 선행 노드들을 알아야 한다. 이를 위해 선형 시간에 구성할 수 있는 역 그래프 의 인접 리스트(Exercise 3.5 참조)가 유용하다. 그러면 의 계산은 의 indegree에 비례하는 시간이 걸리며, 전체 실행 시간은 에 선형적이다. 이는 최대 이며, 입력 배열이 오름차순으로 정렬되어 있을 때 최댓값이 된다. 따라서 동적 프로그래밍 해법은 간단하고 효율적이다.
마지막으로 해결해야 할 문제가 하나 있다: -값은 최적 부분 수열의 길이만 알려주는데, 부분 수열 자체는 어떻게 복구하는가? 이것은 4장에서 최단 경로에 사용했던 것과 동일한 **기록 장치(bookkeeping device)**로 쉽게 관리할 수 있다. 를 계산하는 동안, 로 가는 가장 긴 경로에서 마지막에서 두 번째 노드인 prev도 기록해야 한다. 그러면 이 backpointer들을 따라가면서 최적 부분 수열을 재구성할 수 있다.
6.3 Edit distance
맞춤법 검사기가 오타를 발견하면, 사전에서 가까운 다른 단어를 찾는다. 이 경우 **가까움(closeness)**의 적절한 개념은 무엇일까?
두 문자열 간의 거리를 측정하는 자연스러운 방법은 정렬(alignment), 즉 서로 얼마나 잘 맞춰지는지이다. 기술적으로 정렬은 단순히 문자열을 서로 위아래로 쓰는 방식이다. 예를 들어, SNOWY와 SUNNY의 두 가지 가능한 정렬은 다음과 같다:
| - | 0 | - | 0 | - | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | - |
비용: 3
비용: 5
"-"는 "간격(gap)"을 나타내며, 이들은 어느 문자열에든 원하는 만큼 배치될 수 있다. **정렬의 비용(cost of an alignment)**은 문자가 다른 열의 수이다. 그리고 두 문자열 간의 **편집 거리(edit distance)**는 가능한 최상의 정렬 비용이다. SNOWY와 SUNNY의 정렬 중 비용이 3인 위 정렬보다 더 나은 정렬은 없다는 것을 알 수 있는가?
편집 거리는 첫 번째 문자열을 두 번째 문자열로 변환하는 데 필요한 **최소 편집 횟수(문자 삽입, 삭제, 대체)**로도 생각할 수 있기 때문에 그렇게 이름 붙여졌다. 예를 들어, 왼쪽에 표시된 정렬은 세 가지 편집에 해당한다: U 삽입, 대체, 삭제.
일반적으로 두 문자열 사이에 가능한 정렬이 너무 많아서 최상의 정렬을 찾기 위해 모든 정렬을 검색하는 것은 매우 비효율적일 것이다. 대신 우리는 **동적 프로그래밍(dynamic programming)**을 사용한다.
A dynamic programming solution
동적 프로그래밍으로 문제를 해결할 때 가장 중요한 질문은 "하위 문제(subproblem)는 무엇인가?" 이다. 하위 문제가 다음 속성을 갖도록 선택되는 한,
Recursion? No, thanks.
가장 긴 증가 부분 수열에 대한 논의로 돌아가서: 에 대한 공식은 대안적인 재귀 알고리즘을 제안하기도 한다. 그것이 훨씬 더 간단하지 않을까?
사실, 재귀는 매우 나쁜 생각이다. 그 결과로 나오는 절차는 지수 시간을 필요로 할 것이다! 그 이유를 이해하기 위해, DAG에 모든 에 대해 엣지 가 포함되어 있다고 가정해 보자. 즉, 주어진 숫자 시퀀스 가 정렬되어 있다고 가정해 보자. 이 경우, 하위 문제 에 대한 공식은 다음과 같이 된다.
다음 그림은 에 대한 재귀를 풀어낸다. 동일한 하위 문제들이 계속해서 반복적으로 해결되는 것을 주목하라!
의 경우 이 트리는 지수적으로 많은 노드를 가지므로(이를 제한할 수 있는가?), 재귀적 해결책은 치명적이다.
그렇다면 왜 divide-and-conquer에서는 재귀가 그렇게 잘 작동했을까? 핵심은 divide-and-conquer에서 문제는 상당히 작은 하위 문제, 예를 들어 절반 크기의 하위 문제로 표현된다는 점이다. 예를 들어, mergesort는 크기 의 배열을 크기 의 두 하위 배열을 재귀적으로 정렬함으로써 정렬한다. 문제 크기의 이러한 급격한 감소 때문에 전체 재귀 트리는 로그 깊이와 다항식 수의 노드만을 가진다.
대조적으로, 일반적인 dynamic programming 공식화에서는 문제가 약간만 작은 하위 문제로 축소된다. 예를 들어, 는 에 의존한다. 따라서 전체 재귀 트리는 일반적으로 다항식 깊이와 지수적으로 많은 노드를 가진다. 그러나 이 노드들 대부분은 반복되는 것이며, 그들 중 서로 다른 하위 문제의 수는 그리 많지 않다는 것이 밝혀졌다. 따라서 효율성은 서로 다른 하위 문제들을 명시적으로 열거하고 올바른 순서로 해결함으로써 얻어진다.
Programming?
dynamic programming이라는 용어의 기원은 코드를 작성하는 것과는 거의 관련이 없다. 이 용어는 1950년대 리처드 벨만(Richard Bellman)이 처음 만들었는데, 당시 컴퓨터 프로그래밍은 너무 소수의 사람들만이 행하는 난해한 활동이어서 이름조차 붙일 필요가 없었다. 그때 프로그래밍은 "계획(planning)"을 의미했고, "dynamic programming"은 다단계 프로세스를 최적으로 계획하기 위해 고안되었다. 그림 6.2의 DAG는 이러한 프로세스가 진화할 수 있는 가능한 방법을 설명하는 것으로 생각할 수 있다. 각 노드는 상태를 나타내고, 가장 왼쪽 노드는 시작점이며, 상태에서 나가는 엣지는 가능한 행동을 나타내어 다음 시간 단위에서 다른 상태로 이어진다.
7장의 주제인 linear programming의 어원도 이와 유사하다. (*) 158페이지에서. 알고리즘을 작성하는 것은 쉬운 일이다: 크기가 증가하는 순서대로 하나의 하위 문제를 차례로 반복적으로 해결한다.
우리의 목표는 두 문자열 과 사이의 **편집 거리(edit distance)**를 찾는 것이다. 좋은 하위 문제는 무엇일까? 전체 문제를 해결하는 데 부분적으로 기여해야 한다. 그렇다면 첫 번째 문자열의 접두사 와 두 번째 문자열의 접두사 사이의 편집 거리를 살펴보는 것은 어떨까? 이 하위 문제를 라고 부르자(그림 6.3 참조). 그렇다면 우리의 최종 목표는 을 계산하는 것이다.
이를 위해서는 를 더 작은 하위 문제들로 표현해야 한다. 와 사이의 최적 정렬에 대해 무엇을 알고 있을까? 최적 정렬의 가장 오른쪽 열은 다음 세 가지 중 하나일 수 있다:
| 또는 | - | 또는 | ||
|---|---|---|---|---|
| - | 또는 |
첫 번째 경우는 이 특정 열에 대해 1의 비용이 발생하며, 을 와 정렬하는 것이 남는다. 그런데 이것은 정확히 하위 문제 이다! 우리는 뭔가 진전을 보고 있는 것 같다. 두 번째 경우도 비용이 1이며, 를 과 정렬해야 한다. 이것은 또 다른 하위 문제인 이다. 그리고 마지막 경우, 비용이 1(만약 인 경우) 또는 0(만약 인 경우)이며, 남은 것은 하위 문제 이다. 요컨대, 우리는 를 다음의 세 가지 더 작은 하위 문제로 표현했다.
Figure 6.3 하위 문제 .
| E | X | P | O | N | E | N | T | I | A | L |
|---|---|---|---|---|---|---|---|---|---|---|
| P | O | L | Y | N | O | M | I | A | L |
세 가지 더 작은 하위 문제 로 표현했다. 우리는 이들 중 어느 것이 올바른 것인지 알 수 없으므로, 모두 시도하고 가장 좋은 것을 선택해야 한다:
여기서 편의상 는 이면 0, 그렇지 않으면 1로 정의된다. 예를 들어, EXPONENTIAL과 POLYNOMIAL 사이의 편집 거리를 계산할 때, 하위 문제 은 접두사 EXPO와 POL에 해당한다. 이들의 최적 정렬의 가장 오른쪽 열은 다음 중 하나여야 한다:
| 0 | 또는 | - | 또는 | 0 |
|---|---|---|---|---|
| - | b | L | L | L |
따라서 이다. 모든 하위 문제 의 답은 그림 6.4와 같이 2차원 테이블을 형성한다. 이 하위 문제들은 어떤 순서로 해결되어야 할까? , 그리고 이 보다 먼저 처리되는 한 어떤 순서든 상관없다. 예를 들어, 테이블을 한 번에 한 행씩, 위쪽 행에서 아래쪽 행으로, 그리고 각 행을 왼쪽에서 오른쪽으로 이동하면서 채울 수 있다. 또는 열별로 채울 수도 있다. 두 방법 모두 특정 테이블 항목을 계산할 때 필요한 다른 모든 항목이 이미 채워져 있도록 보장한다.
하위 문제와 순서가 모두 지정되었으므로 거의 완료되었다. 이제 dynamic programming의 "기본 사례(base cases)", 즉 가장 작은 하위 문제들만 남았다. 현재 상황에서 이들은 와 이며, 둘 다 쉽게 해결된다. 는 의 길이가 0인 접두사, 즉 빈 문자열과 의 첫 개 문자 사이의 편집 거리이다. 분명히 이다. 마찬가지로 이다.
Figure 6.4 (a) 하위 문제 테이블. 를 채우기 위해 , 그리고 항목이 필요하다. (b) dynamic programming으로 찾은 최종 값 테이블.
(a)
 (b)
(b)
| P | O | L | Y | N | O | M | I | A | L | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| E | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| X | 2 | 2 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| P | 3 | 2 | 3 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| O | 4 | 3 | 2 | 3 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |
| N | 5 | 4 | 3 | 3 | 4 | 4 | 5 | 6 | 7 | 8 | 9 |
| E | 6 | 5 | 4 | 4 | 4 | 5 | 5 | 6 | 7 | 8 | 9 |
| N | 7 | 6 | 5 | 5 | 5 | 4 | 5 | 6 | 7 | 8 | 9 |
| T | 8 | 7 | 6 | 6 | 6 | 5 | 5 | 6 | 7 | 8 | 9 |
| I | 9 | 8 | 7 | 7 | 7 | 6 | 6 | 6 | 6 | 7 | 8 |
| A | 10 | 9 | 8 | 8 | 8 | 7 | 7 | 7 | 7 | 6 | 7 |
| L | 11 | 10 | 9 | 8 | 9 | 8 | 8 | 8 | 8 | 7 | 6 |
이 시점에서 편집 거리 알고리즘은 기본적으로 저절로 작성된다.
for \(i=0,1,2, \ldots, m\) :
\(E(i, 0)=i\)
for \(j=1,2, \ldots, n\) :
\(E(0, j)=j\)
for \(i=1,2, \ldots, m\) :
for \(j=1,2, \ldots, n\) :
\(E(i, j)=\min \{E(i-1, j)+1, E(i, j-1)+1, E(i-1, j-1)+\operatorname{diff}(i, j)\}\)
return \(E(m, n)\)
이 절차는 테이블을 행별로, 그리고 각 행 내에서 왼쪽에서 오른쪽으로 채운다. 각 항목을 채우는 데는 상수 시간이 걸리므로, 전체 실행 시간은 테이블의 크기인 이다.
그리고 우리 예시에서 편집 거리는 6으로 밝혀졌다:
| 0 | - | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| - | - | 0 | 0 |
The underlying dag
모든 **동적 프로그래밍(dynamic program)**은 기저에 DAG(directed acyclic graph) 구조를 가지고 있다. 각 노드를 하위 문제(subproblem)로, 각 엣지를 하위 문제를 해결할 수 있는 순서에 대한 선행 제약 조건(precedence constraint)으로 생각할 수 있다. 노드 가 를 가리킨다는 것은 "하위 문제 는 에 대한 답을 알게 된 후에만 해결될 수 있다"는 의미이다.
현재 편집 거리(edit distance) 애플리케이션에서, 기저 DAG의 노드는 하위 문제, 또는 동일하게 테이블의 위치 에 해당한다. DAG의 엣지는 , , 그리고 형태의 선행 제약 조건이다 (Figure 6.5). 사실, 여기서 한 걸음 더 나아가 엣지에 가중치를 부여하여 편집 거리가 DAG의 **최단 경로(shortest paths)**로 주어지도록 할 수 있다! 이를 위해, (그림에서 점선으로 표시됨)를 제외한 모든 엣지 길이를 1로 설정하고, 해당 엣지의 길이는 0으로 설정한다. 그러면 최종 답은 단순히 노드 와 사이의 거리가 된다. 이전에 찾았던 정렬(alignment)을 생성하는 하나의 가능한 최단 경로가 그림에 표시되어 있다. 이 경로에서 아래로 이동하는 각 동작은 삭제(deletion), 오른쪽으로 이동하는 각 동작은 삽입(insertion), 그리고 대각선으로 이동하는 각 동작은 일치(match) 또는 **대체(substitution)**이다.
이 DAG의 가중치를 변경함으로써, 삽입, 삭제, 대체에 서로 다른 비용이 할당되는 **일반화된 형태의 편집 거리(generalized forms of edit distance)**를 허용할 수 있다.
Figure 6.5 기저 DAG와 길이 6의 경로.

6.4 Knapsack
강도가 강도 중에 예상보다 훨씬 많은 전리품을 발견하고 무엇을 가져갈지 결정해야 한다. 그의 가방(또는 "knapsack")은 총 최대 파운드의 무게를 담을 수 있다. 선택할 수 있는 개의 아이템이 있으며, 각 아이템의 무게는 이고 달러 가치는 이다. 가방에 넣을 수 있는 아이템들의 가장 가치 있는 조합은 무엇일까?
예를 들어, 이고 다음과 같은 아이템들이 있다고 가정해 보자.
| 아이템 | 무게 | 가치 |
|---|---|---|
| 1 | 6 | \ 30$ |
| 2 | 3 | \ 14$ |
| 3 | 4 | \ 16$ |
| 4 | 2 | \ 9$ |
Common subproblems
올바른 subproblem을 찾는 것은 창의력과 실험이 필요한 일이다. 하지만 dynamic programming에서 반복적으로 나타나는 몇 가지 표준적인 선택지가 있다.
i. 입력은 이고, subproblem은 이다.
따라서 subproblem의 수는 선형적이다. ii. 입력은 과 이다. subproblem은 와 이다.
subproblem의 수는 이다. iii. 입력은 이고, subproblem은 이다.
subproblem의 수는 이다.
iv. 입력은 rooted tree이다. subproblem은 rooted subtree이다.
트리에 개의 노드가 있다면, subproblem의 수는 몇 개일까?
우리는 이미 처음 두 가지 경우를 접했으며, 다른 경우들은 곧 다루게 될 것이다.
Of mice and men
우리 몸은 기능적으로 유연하고, 새로운 환경에 적응하며, 상호작용하고 번식할 수 있는 놀라운 기계이다. 이러한 모든 능력은 우리 각자에게 고유한 프로그램, 즉 알파벳으로 구성된 30억 자 길이의 문자열인 DNA에 의해 결정된다.
두 사람의 DNA 서열은 약 0.1%만 다르다. 그러나 이 작은 차이에도 불구하고 3백만 개의 위치에서 변이가 발생하며, 이는 인간 다양성의 광범위한 범위를 설명하기에 충분하다. 이러한 차이점은 과학적, 의학적으로 큰 관심을 끈다. 예를 들어, 특정 질병에 취약한 사람들을 예측하는 데 도움이 될 수 있다.
DNA는 방대하고 겉보기에는 이해하기 어려운 프로그램이지만, 서브루틴처럼 역할이 더 구체적인 작은 단위로 나눌 수 있다. 이를 **유전자(genes)**라고 한다. 컴퓨터는 인간 및 다른 유기체의 유전자를 이해하는 데 중요한 도구가 되었으며, **계산 유전체학(computational genomics)**은 이제 독립적인 분야로 자리 잡았다. 다음은 발생하는 일반적인 질문의 예시이다.
- 새로운 유전자가 발견되면, 그 기능을 이해하는 한 가지 방법은 밀접하게 일치하는 알려진 유전자를 찾는 것이다. 이는 쥐와 같이 잘 연구된 종의 지식을 인간에게 이전하는 데 특히 유용하다. 이러한 검색 문제의 기본적인 원시 연산은 두 문자열이 대략적으로 일치하는 시점을 효율적으로 계산할 수 있는 개념을 정의하는 것이다. 생물학적 관점은 edit distance의 일반화를 제안하며, dynamic programming을 사용하여 이를 계산할 수 있다. 그다음에는 알려진 유전자들의 방대한 숲을 검색하는 문제가 있다. GenBank 데이터베이스는 이미 총 길이가 을 넘으며, 이 숫자는 빠르게 증가하고 있다. 현재 가장 선호되는 방법은 BLAST이다. 이는 알고리즘적 기법과 생물학적 직관의 영리한 조합으로, 계산 생물학에서 가장 널리 사용되는 소프트웨어가 되었다.
- DNA 시퀀싱(즉, DNA를 구성하는 문자열을 결정하는 것) 방법은 일반적으로 자 길이의 **조각(fragments)**만 찾아낸다. 수십억 개의 무작위로 흩어진 조각들을 생성할 수 있지만, 이들을 어떻게 일관된 DNA 서열로 조립할 수 있을까? 우선, 최종 서열에서 어떤 조각의 위치도 알 수 없으며, 겹치는 조각들을 이어 붙여서 추론해야 한다. 이러한 노력의 대표적인 예시는 2001년에 두 그룹이 동시에 완성한 인간 DNA 초안이다: 공공 자금으로 운영되는 Human Genome Consortium과 민간 기업인 Celera Genomics.
- 특정 유전자가 여러 종에서 각각 시퀀싱되었을 때, 이 정보를 사용하여 이들 종의 진화 역사를 재구성할 수 있을까? 우리는 이 장의 끝에 있는 연습 문제에서 이러한 문제들을 탐구할 것이다. dynamic programming은 이들 중 일부와 계산 생물학 전반에 걸쳐 매우 귀중한 도구임이 밝혀졌다.
이 문제에는 두 가지 버전이 있다. 각 품목이 무제한으로 제공되는 경우, 최적의 선택은 품목 1과 품목 4 두 개를 선택하는 것이다(총: ). 반면에 각 품목이 하나씩만 있는 경우(예를 들어, 도둑이 미술관에 침입한 경우), 최적의 배낭에는 품목 1과 3이 포함된다(총: ).
8장에서 보겠지만, 이 문제의 어떤 버전도 다항 시간 알고리즘을 가질 가능성은 낮다. 그러나 dynamic programming을 사용하면 둘 다 시간에 해결할 수 있다. 이는 가 작을 때는 합리적이지만, 입력 크기가 가 아닌 에 비례하므로 다항 시간이 아니다.
Knapsack with repetition
반복을 허용하는 버전부터 시작해 보자. 언제나 그렇듯이, 동적 프로그래밍의 주요 질문은 **하위 문제(subproblems)**가 무엇인가 하는 것이다. 이 경우, 우리는 원래 문제를 두 가지 방식으로 축소할 수 있다: 더 작은 배낭 용량 를 고려하거나, 더 적은 수의 아이템(예: 인 아이템 )을 고려하는 것이다. 어떤 방식이 정확히 작동하는지 파악하려면 약간의 실험이 필요하다.
첫 번째 제약 조건은 더 작은 용량을 요구한다. 따라서 다음과 같이 정의한다:
이것을 더 작은 하위 문제로 표현할 수 있을까? 만약 에 대한 최적해가 아이템 를 포함한다면, 이 아이템을 배낭에서 제거하면 에 대한 최적해가 남는다. 다시 말해, 는 어떤 에 대해 단순히 이다. 우리는 어떤 인지 모르므로, 모든 가능성을 시도해야 한다.
여기서 평소와 같이 빈 집합에 대한 최댓값은 0으로 간주한다. 끝났다! 이제 알고리즘은 저절로 작성되며, 특징적으로 간단하고 우아하다.
\(K(0)=0\)
for \(w=1\) to \(W\) :
\(K(w)=\max \left\{K\left(w-w_{i}\right)+v_{i}: w_{i} \leq w\right\}\)
return \(K(W)\)
이 알고리즘은 길이 의 1차원 테이블을 왼쪽에서 오른쪽 순서로 채운다. 각 항목을 계산하는 데는 최대 시간이 걸릴 수 있으므로, 전체 실행 시간은 이다.
언제나 그렇듯이, **기저 DAG(directed acyclic graph)**가 존재한다. 이를 구성해 보면 놀라운 통찰력을 얻게 될 것이다: 이 특정 knapsack 변형은 DAG에서 가장 긴 경로를 찾는 문제로 귀결된다!
Knapsack without repetition
두 번째 변형으로 넘어가서, 만약 반복이 허용되지 않는다면 어떻게 될까? 우리의 이전 하위 문제들은 이제 완전히 쓸모없게 된다. 예를 들어, 값이 매우 높다는 것을 아는 것은 우리에게 도움이 되지 않는다. 왜냐하면 항목 이 이 부분 해에서 이미 사용되었는지 여부를 알 수 없기 때문이다. 따라서 우리는 사용되는 항목에 대한 추가 정보를 포함하도록 하위 문제의 개념을 다듬어야 한다. 우리는 두 번째 매개변수 를 추가한다:
용량 의 배낭과 항목 를 사용하여 달성할 수 있는 최대 가치.
우리가 찾는 답은 이다.
하위 문제 를 더 작은 하위 문제들로 어떻게 표현할 수 있을까? 아주 간단하다: 최적의 가치를 달성하기 위해 항목 가 필요하거나, 필요하지 않거나 둘 중 하나이다:
(첫 번째 경우는 일 때만 호출된다.) 다시 말해, 우리는 를 하위 문제 로 표현할 수 있다.
알고리즘은 개의 행과 개의 열을 가진 2차원 테이블을 채우는 것으로 구성된다. 각 테이블 항목은 상수 시간만 소요되므로, 테이블이 이전 경우보다 훨씬 크더라도 실행 시간은 로 동일하게 유지된다. 코드는 다음과 같다.
Initialize all \(K(0, j)=0\) and all \(K(w, 0)=0\)
for \(j=1\) to \(n\) :
for \(w=1\) to \(W\) :
if \(w_{j}>w: K(w, j)=K(w, j-1)\)
else: \(K(w, j)=\max \left\{K(w, j-1), K\left(w-w_{j}, j-1\right)+v_{j}\right\}\)
return \(K(W, n)\)
6.5 Chain matrix multiplication
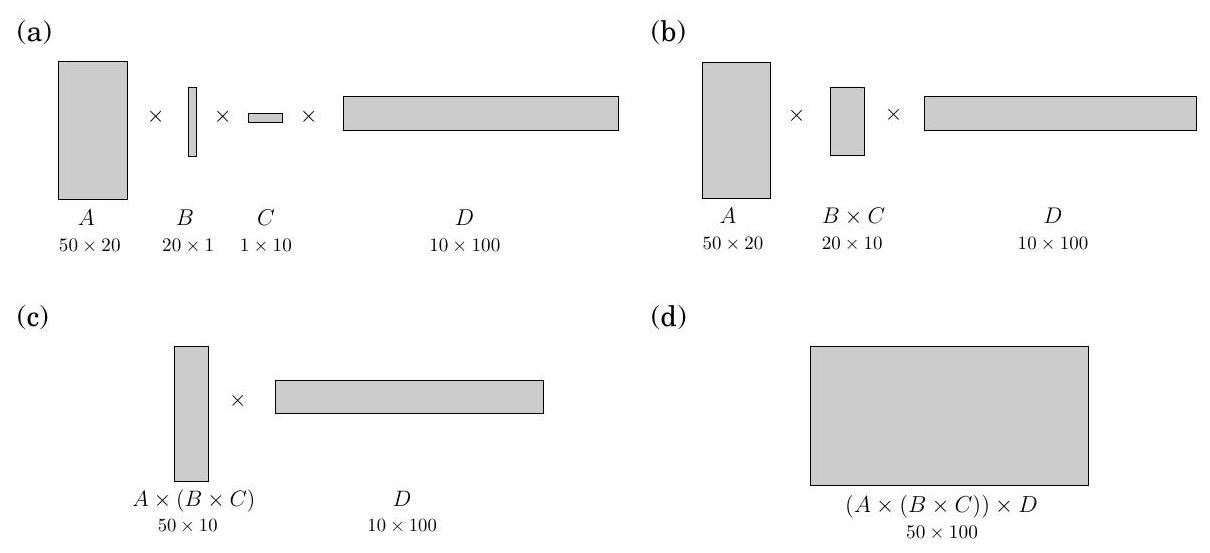
차원의 네 행렬 를 곱한다고 가정해 보자(Figure 6.6). 이 과정은 한 번에 두 행렬을 반복적으로 곱하는 것을 포함한다. 행렬 곱셈은
Figure 6.6 .
Memoization
**동적 계획법(dynamic programming)**에서는 큰 문제를 작은 문제로 표현하는 재귀 공식을 작성한 다음, 가장 작은 하위 문제부터 가장 큰 하위 문제까지 상향식(bottom-up) 방식으로 해답 값 테이블을 채워 나간다.
이 공식은 재귀 알고리즘을 제안하기도 하지만, 이전에 살펴보았듯이 **순진한 재귀(naive recursion)**는 동일한 하위 문제를 반복해서 해결하기 때문에 매우 비효율적일 수 있다. 그렇다면 이전 호출을 기억하여 반복을 피하는 더 지능적인 재귀 구현은 어떨까?
배낭 문제(knapsack problem)(반복 허용)의 경우, 이러한 알고리즘은 해시 테이블(섹션 1.5 참조)을 사용하여 이미 계산된 값을 저장한다. 를 요청하는 각 재귀 호출에서 알고리즘은 먼저 해시 테이블에 답이 있는지 확인하고, 없는 경우에만 계산을 진행한다. 이 기법을 **메모이제이션(memoization)**이라고 한다:
A hash table, initially empty, holds values of \(K(w)\) indexed by \(w\)
function knapsack ( \(w\) )
if \(w\) is in hash table: return \(K(w)\)
\(K(w)=\max \left\{\operatorname{knapsack}\left(w-w_{i}\right)+v_{i}: w_{i} \leq w\right\}\)
insert \(K(w)\) into hash table, with key \(w\)
return \(K(w)\)
이 알고리즘은 하위 문제를 반복하지 않으므로, 실행 시간은 동적 계획법과 마찬가지로 이다. 그러나 재귀의 오버헤드 때문에 이 **빅-O 표기법(big-O notation)**의 상수 인자는 상당히 더 크다.
하지만 어떤 경우에는 메모이제이션이 효과를 발휘한다. 그 이유는 다음과 같다: 동적 계획법은 잠재적으로 필요할 수 있는 모든 하위 문제를 자동으로 해결하는 반면, 메모이제이션은 실제로 사용되는 문제만 해결한다. 예를 들어, 와 모든 가중치 가 100의 배수라고 가정해 보자. 그러면 100이 를 나누지 않으면 하위 문제 는 쓸모가 없다. 메모이제이션된 재귀 알고리즘은 이러한 불필요한 테이블 항목을 전혀 보지 않을 것이다. (일반적으로 )이지만, **결합적(associative)**이므로 예를 들어 이다. 따라서 네 개의 행렬 곱셈은 괄호를 어떻게 묶느냐에 따라 여러 가지 방법으로 계산할 수 있다. 이들 중 일부가 다른 것보다 더 나을까?
행렬과 행렬을 곱하는 데는 번의 곱셈이 필요하다는 것이 충분히 좋은 근사치이다. 이 공식을 사용하여 를 평가하는 여러 가지 방법을 비교해 보자:
| Parenthesization | Cost computation | Cost |
|---|---|---|
| 120,200 | ||
| 60,200 | ||
| 7,000 |
보시다시피, 곱셈 순서는 최종 실행 시간에 큰 차이를 만든다! 더욱이, 항상 가장 저렴한 행렬 곱셈을 수행하는 자연스러운 그리디(greedy) 접근 방식은 여기에 표시된 두 번째 괄호 묶음으로 이어지므로 실패한다.
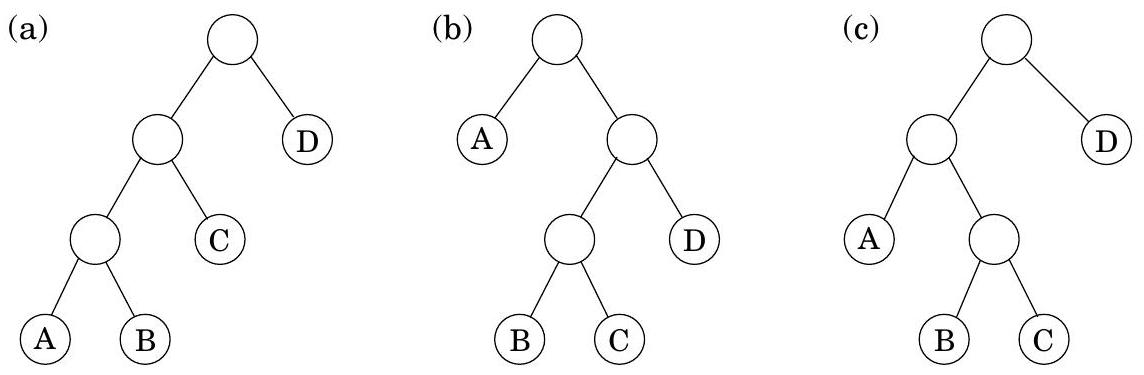
을 계산할 때 최적의 순서를 어떻게 결정할까? 여기서 는 각각 차원을 가진 행렬이다. 가장 먼저 주목할 점은 특정 괄호 묶음이 **이진 트리(binary tree)**로 매우 자연스럽게 표현될 수 있다는 것이다. 이 트리에서 개별 행렬은 **리프(leaves)**에 해당하고, **루트(root)**는 최종 곱셈이며, **내부 노드(interior nodes)**는 중간 곱셈이다(Figure 6.7). 곱셈을 수행할 수 있는 가능한 순서는 개의 리프를 가진 다양한 **완전 이진 트리(full binary trees)**에 해당하며, 그 수는 에 대해 **지수적(exponential)**이다(연습 문제 2.13). 우리는 분명히 모든 트리를 시도할 수 없으며, **무차별 대입(brute force)**이 배제되었으므로 동적 계획법으로 전환한다.
Figure 6.7의 이진 트리는 시사하는 바가 있다: 트리가 최적이라면, 그 **서브트리(subtrees)**도 최적이어야 한다. 서브트리에 해당하는 하위 문제는 무엇일까? 그것들은 형태의 곱셈이다. 이것이 작동하는지 살펴보자: 에 대해 다음을 정의한다.
이 하위 문제의 크기는 행렬 곱셈의 수인 이다. 가장 작은 하위 문제는 일 때이며, 이 경우 곱할 것이 없으므로 이다. 인 경우, 에 대한 최적의 서브트리를 고려해 보자. 이 서브트리의 첫 번째 분기, 즉 맨 위 분기는 곱셈을 와 의 두 부분으로 나눌 것이다. 여기서 는 와 사이의 어떤 값이다. 서브트리의 비용은 이 두 부분 곱셈의 비용과 이들을 결합하는 비용의 합이다: . 그리고 우리는 이것이 가장 작은 분할점 를 찾아야 한다:
이제 코드를 작성할 준비가 되었다! 다음 코드에서 변수 는 하위 문제의 크기를 나타낸다.
for \(i=1\) to \(n: \quad C(i, i)=0\)
for \(s=1\) to \(n-1\) :
for \(i=1\) to \(n-s\) :
\(j=i+s\)
\(C(i, j)=\min \left\{C(i, k)+C(k+1, j)+m_{i-1} \cdot m_{k} \cdot m_{j}: i \leq k<j\right\}\)
return \(C(1, n)\)
하위 문제들은 2차원 테이블을 구성하며, 각 항목을 계산하는 데 시간이 걸린다. 따라서 전체 실행 시간은 이다.
Figure 6.7 (a) ; (b) ;
(c) .
6.6 Shortest paths
우리는 이 장을 DAG에서 최단 경로를 찾는 기본적인 task를 위한 동적 프로그래밍 알고리즘으로 시작했다. 이제 더 정교한 최단 경로 문제로 넘어가서 이러한 문제들도 우리의 강력한 알고리즘 기법으로 어떻게 해결할 수 있는지 살펴본다.
Shortest reliable paths
삶은 복잡하며, 그래프, 엣지 길이, 최단 경로와 같은 추상적인 개념들이 전체 진실을 포착하는 경우는 드물다. 예를 들어, 통신 네트워크에서 엣지 길이가 전송 지연을 충실히 반영하더라도 경로를 선택하는 데 다른 고려 사항이 있을 수 있다. 예를 들어, 경로의 각 추가 엣지는 패킷 손실의 불확실성과 위험이 따르는 추가적인 "홉(hop)"일 수 있다. 이러한 경우, 우리는 너무 많은 엣지를 가진 경로를 피하고 싶을 것이다. 그림 6.8은 이 문제를 설명하는 그래프를 보여준다. 이 그래프에서 에서 까지의 최단 경로는 네 개의 엣지를 가지는 반면, 약간 더 길지만 두 개의 엣지만 사용하는 다른 경로가 있다. 만약 네 개의 엣지가 감당할 수 없는 불안정성을 의미한다면, 우리는 후자의 경로를 선택해야 할 수도 있다.
그림 6.8 우리는 짧고 엣지 수가 적은 에서 까지의 경로를 원한다.
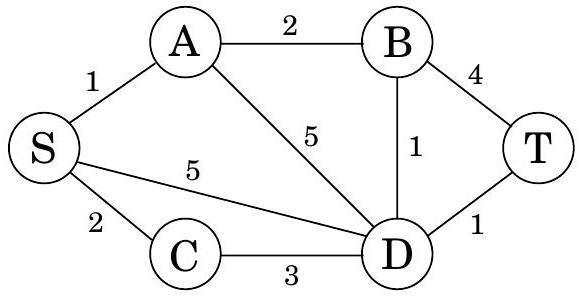
그렇다면 엣지에 길이가 부여된 그래프 와 두 노드 , , 그리고 정수 가 주어졌을 때, 최대 개의 엣지를 사용하는 에서 까지의 최단 경로를 찾는다고 가정해 보자.
이 새로운 task에 Dijkstra 알고리즘을 빠르게 적용할 수 있는 방법이 있을까? 그렇지는 않다. 이 알고리즘은 경로의 홉 수를 "기억"하지 않고 각 최단 경로의 길이에만 초점을 맞추는데, 홉 수는 이제 중요한 정보가 되었다.
동적 프로그래밍에서 핵심은 모든 중요한 정보가 기억되고 다음 단계로 전달되도록 **하위 문제(subproblems)**를 선택하는 것이다. 이 경우, 각 정점 와 각 정수 에 대해, **dist()**를 개의 엣지를 사용하는 에서 까지의 최단 경로의 길이라고 정의하자. 시작 값 dist()는 를 제외한 모든 정점에 대해 이고, 에 대해서는 0이다. 그리고 일반적인 업데이트 방정식은 당연하게도 다음과 같다.
더 설명할 필요가 있을까?
All-pairs shortest paths
와 뿐만 아니라 모든 정점 쌍 사이의 최단 경로를 찾고 싶다면 어떻게 해야 할까? 한 가지 접근 방식은 (음수 간선이 있을 수 있으므로) 4.6.1절의 일반적인 최단 경로 알고리즘을 각 시작 노드에 대해 한 번씩, 총 번 실행하는 것이다. 그러면 총 실행 시간은 가 된다. 이제 우리는 더 나은 대안인 동적 프로그래밍 기반 Floyd-Warshall 알고리즘을 살펴볼 것이다.
그래프의 모든 정점 쌍 사이의 거리를 계산하는 데 적합한 subproblem이 있을까? 단순히 점점 더 많은 쌍이나 시작점에 대해 문제를 푸는 것은 도움이 되지 않는다. 왜냐하면 이는 알고리즘으로 다시 돌아가기 때문이다.
한 가지 아이디어가 떠오른다: 와 사이의 최단 경로 는 여러 개의 중간 노드를 사용한다(아마도 없을 수도 있다). 중간 노드를 전혀 허용하지 않는다고 가정해 보자. 그러면 모든 쌍 최단 경로를 한 번에 해결할 수 있다: 에서 까지의 최단 경로는 존재하는 경우 단순히 직접적인 간선 이다. 이제 허용되는 중간 노드 집합을 점진적으로 확장하면 어떻게 될까? 우리는 한 번에 하나의 노드씩 이 작업을 수행하여 각 단계에서 최단 경로 길이를 업데이트할 수 있다. 결국 이 집합은 전체로 확장되고, 이 시점에는 모든 정점이 모든 경로에 허용되며, 우리는 그래프 정점 사이의 진정한 최단 경로를 찾게 된다!
더 구체적으로, 의 정점들에 으로 번호를 매기고, 를 중간 노드로 만 사용할 수 있는 에서 까지의 최단 경로 길이라고 하자. 초기에는 는 와 사이의 직접적인 간선 길이가 존재하면 그 길이고, 그렇지 않으면 이다.
중간 집합을 확장하여 추가 노드 를 포함하면 어떻게 될까? 우리는 모든 쌍 를 다시 검토하고 를 중간 지점으로 사용하는 것이 에서 까지 더 짧은 경로를 제공하는지 확인해야 한다. 하지만 이것은 쉽다: 와 다른 낮은 번호의 중간 노드를 사용하여 에서 까지 가는 최단 경로는 를 한 번만 통과한다(왜냐하면 음수 사이클이 없다고 가정하기 때문이다). 그리고 우리는 이미 낮은 번호의 정점만 사용하여 에서 까지, 그리고 에서 까지의 최단 경로 길이를 계산했다:
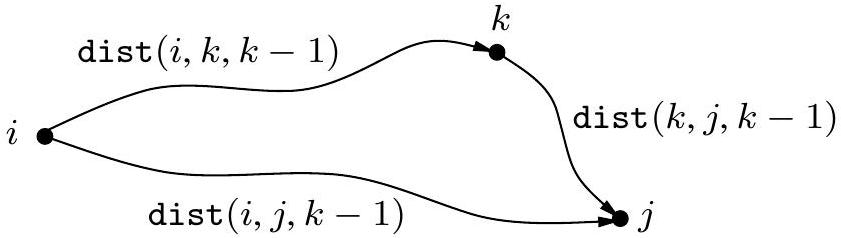
따라서 를 사용하는 것이 에서 까지 더 짧은 경로를 제공하는 경우는 다음과 같을 때뿐이다.
이 경우 는 그에 따라 업데이트되어야 한다. 다음은 Floyd-Warshall 알고리즘이며, 보시다시피 시간이 소요된다.
for i=1 to n:
for j=1 to n:
dist(i,j,0)=\infty
for all (i,j)\inE:
dist(i,j,0)=\ell(i,j)
for k=1 to n:
for i=1 to n:
for j=1 to n:
dist(i, j,k)=min{dist(i,k,k-1)+dist(k,j,k-1), dist(i,j,k-1)}
The traveling salesman problem
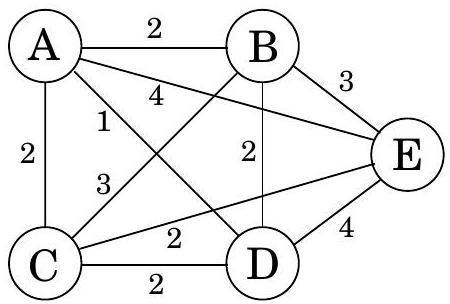
한 외판원이 대규모 판매 투어를 준비하고 있다. 고향에서 여행 가방을 들고 출발하여, 각 목표 도시를 정확히 한 번씩 방문한 후 집으로 돌아오는 여정을 수행할 것이다. 도시 간의 쌍별 거리가 주어졌을 때, 전체 이동 거리를 최소화하기 위해 도시들을 방문하는 가장 좋은 순서는 무엇일까?
도시들을 으로 나타내고, 외판원의 고향을 1이라고 하자. 그리고 도시 간 거리 행렬을 라고 하자. 목표는 1에서 시작하여 1에서 끝나고, 다른 모든 도시를 정확히 한 번씩 포함하며, 총 길이가 최소인 투어를 설계하는 것이다. 그림 6.9는 다섯 개 도시를 포함하는 예시를 보여준다. 최적의 투어를 찾을 수 있는가? 이 작은 예시에서도 사람이 해결책을 찾는 것은 까다롭다. 수백 개의 도시가 포함될 때 어떤 일이 벌어질지 상상해 보라.
이 문제는 컴퓨터에게도 어려운 것으로 밝혀졌다. 사실, **외판원 문제(Traveling Salesman Problem, TSP)**는 가장 악명 높은 계산 문제 중 하나이다. 이 문제를 해결하려는 시도는 오랜 역사를 가지고 있으며, 실패와 부분적인 성공의 긴 서사시를 거쳐 알고리즘 및 복잡성 이론에 큰 발전을 가져왔다. TSP에 대한 가장 기본적인
그림 6.9 최적의 외판원 투어는 길이가 10이다.
나쁜 소식은, 8장에서 더 잘 이해하겠지만, 다항 시간(polynomial time) 내에 해결될 가능성이 매우 낮다는 것이다.
그렇다면 얼마나 오래 걸릴까? 무차별 대입(brute-force) 방식은 가능한 모든 투어를 평가하고 가장 좋은 것을 반환하는 것이다. 가지 가능성이 있으므로, 이 전략은 시간이 걸린다. 이제 **동적 프로그래밍(dynamic programming)**이 다항 시간은 아니지만 훨씬 빠른 해결책을 제공한다는 것을 알게 될 것이다.
TSP에 적합한 **하위 문제(subproblem)**는 무엇일까? 하위 문제는 부분적인 해결책을 의미하며, 이 경우 가장 명확한 부분적인 해결책은 투어의 초기 부분이다. 요구 사항에 따라 도시 1에서 시작하여 몇 개의 도시를 방문했고, 현재 도시 에 있다고 가정해 보자. 이 부분적인 투어를 확장하기 위해 어떤 정보가 필요할까? 다음으로 방문하기 가장 편리한 도시를 결정할 것이므로 를 알아야 한다. 그리고 지금까지 방문한 모든 도시를 알아야 중복 방문을 피할 수 있다. 따라서 적절한 하위 문제는 다음과 같다.
도시들의 부분집합 에 1이 포함되고 일 때, 를 1에서 시작하여 에서 끝나고 의 각 노드를 정확히 한 번씩 방문하는 최단 경로의 길이라고 하자.
일 때, 경로는 1에서 시작하고 1에서 끝날 수 없으므로 로 정의한다.
이제 를 더 작은 하위 문제들로 표현해 보자. 1에서 시작하여 에서 끝나야 한다. 두 번째로 마지막 도시로 무엇을 선택해야 할까? 그것은 에 있는 어떤 여야 하므로, 전체 경로 길이는 1에서 까지의 거리, 즉 에 마지막 간선 의 길이를 더한 것이다. 우리는 그러한 중에서 가장 좋은 것을 선택해야 한다:
On time and memory
동적 프로그래밍(dynamic programming) 알고리즘의 실행 시간은 **서브문제(subproblem)의 DAG(Directed Acyclic Graph)**를 통해 쉽게 파악할 수 있다. 많은 경우, 이는 단순히 DAG의 총 간선(edge) 수와 같다! 우리가 실제로 하는 일은 노드를 선형화된 순서로 방문하고, 각 노드의 in-edge를 검사하며, 대부분의 경우 각 간선당 일정한 양의 작업을 수행하는 것이다. 결국 DAG의 각 간선은 한 번씩 검사된다.
하지만 필요한 컴퓨터 메모리 양은 얼마나 될까? 이를 특징짓는 간단한 DAG 매개변수는 없다. 서브문제의 수에 비례하는 메모리로 작업을 수행하는 것은 확실히 가능하지만, 보통은 훨씬 적은 양으로도 가능하다. 그 이유는 특정 서브문제의 값은 해당 서브문제에 의존하는 더 큰 서브문제들이 해결될 때까지만 기억하면 되기 때문이다. 그 이후에는 해당 메모리를 재사용을 위해 해제할 수 있다.
예를 들어, Floyd-Warshall 알고리즘에서 값은 값들이 계산되면 더 이상 필요하지 않다. 따라서 값을 저장하기 위해 두 개의 배열만 있으면 된다. 하나는 의 홀수 값용이고 다른 하나는 짝수 값용이다. 를 계산할 때, 우리는 를 덮어쓴다. (그리고 동적 프로그래밍에서 항상 그렇듯이, 현재 에서 까지의 최단 경로에서 마지막에서 두 번째 정점(vertex)을 저장하는 라는 배열이 하나 더 필요하다는 것을 잊지 말자. 이 값은 와 함께 업데이트되어야 한다. 우리는 이 평범하지만 중요한 기록 관리 단계를 동적 프로그래밍 알고리즘에서 생략한다.)
그림 6.5의 편집 거리(edit distance) DAG가 왜 더 짧은 문자열의 길이에 비례하는 메모리만 필요한지 알 수 있는가?
서브문제는 에 따라 정렬된다. 코드는 다음과 같다.
\(C(\{1\}, 1)=0\)
for \(s=2\) to \(n\) :
for all subsets \(S \subseteq\{1,2, \ldots, n\}\) of size \(s\) and containing 1:
\(C(S, 1)=\infty\)
for all \(j \in S, j \neq 1\) :
\(C(S, j)=\min \left\{C(S-\{j\}, i)+d_{i j}: i \in S, i \neq j\right\}\)
return \(\min _{j} C(\{1, \ldots, n\}, j)+d_{j 1}\)
최대 개의 서브문제가 있으며, 각 서브문제를 해결하는 데 선형 시간이 걸린다. 따라서 총 실행 시간은 이다.
6.7 Independent sets in trees
노드들의 부분집합 가 그래프 의 independent set이라는 것은 그 노드들 사이에 엣지가 없다는 의미이다. 예를 들어, 그림 6.10에서 노드 는 independent set을 형성하지만, 노드 는 4와 5 사이에 엣지가 있기 때문에 independent set이 아니다. 가장 큰 independent set은 이다.
Figure 6.10 이 그래프에서 가장 큰 independent set의 크기는 3이다.
이 장에서 보았던 다른 여러 문제들(knapsack, traveling salesman)과 마찬가지로, 그래프에서 가장 큰 independent set을 찾는 것은 다루기 힘든(intractable) 문제로 알려져 있다. 그러나 그래프가 tree인 경우에는 **동적 프로그래밍(dynamic programming)**을 사용하여 선형 시간 안에 문제를 해결할 수 있다. 그렇다면 적절한 하위 문제(subproblem)는 무엇일까? chain matrix multiplication 문제에서 이미 우리는 tree의 계층적 구조가 하위 문제의 자연스러운 정의를 제공한다는 것을 알았다. 단, tree의 한 노드가 root로 식별되어야 한다.
따라서 알고리즘은 다음과 같다: 임의의 노드 을 root로 하여 tree를 시작한다. 이제 각 노드는 자신으로부터 뻗어 나가는 subtree를 정의한다. 이는 즉시 하위 문제를 제안한다:
우리의 최종 목표는 이다. 동적 프로그래밍은 항상 작은 하위 문제에서 큰 하위 문제로 진행된다. 즉, rooted tree에서 bottom-up 방식으로 진행된다. 특정 노드 아래의 모든 subtree에 대해 가장 큰 independent set을 알고 있다고 가정해 보자. 다시 말해, 의 모든 자손 에 대해 를 알고 있다고 가정해 보자. 를 어떻게 계산할 수 있을까? 계산을 두 가지 경우로 나누어 보자: 어떤 independent set이 를 포함하거나 포함하지 않는 경우(그림 6.11).
만약 independent set이 를 포함한다면, 에 대해 1점을 얻지만, 의 자식들은 포함할 수 없다. 따라서 손자들로 넘어간다. 이것이 공식의 첫 번째 경우이다. 반면에 를 포함하지 않는다면, 에 대해 점수를 얻지 못하지만, 의 자식들로 넘어갈 수 있다.
하위 문제의 수는 정확히 정점의 수와 같다. 약간의 주의를 기울이면 실행 시간은 선형 시간인 로 만들 수 있다.
Figure 는 를 root로 하는 subtree의 가장 큰 independent set의 크기이다. 두 가지 경우: 가 이 independent set에 포함되거나, 포함되지 않는 경우.
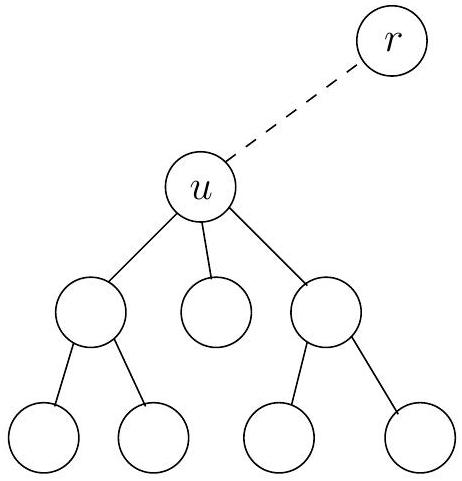
Exercises
6.1. 리스트 의 **연속 부분 수열(contiguous subsequence)**은 의 연속적인 요소들로 구성된 부분 수열이다. 예를 들어, 가 다음과 같을 때:
은 연속 부분 수열이지만 은 아니다. 다음 task에 대한 선형 시간 알고리즘을 제시하시오:
입력: 숫자 리스트 . 출력: 합이 최대가 되는 연속 부분 수열 (길이가 0인 부분 수열의 합은 0이다). 위 예시의 경우, 답은 이며 합은 55이다. (힌트: 각 에 대해, 정확히 위치 에서 끝나는 연속 부분 수열을 고려하시오.)
6.2. 당신은 장거리 여행을 떠난다. 0마일 지점에서 출발한다. 도중에 개의 호텔이 마일 지점 에 있으며, 각 는 출발 지점으로부터 측정된 거리이다. 당신이 멈출 수 있는 유일한 장소는 이 호텔들이지만, 어떤 호텔에 멈출지는 선택할 수 있다. 당신은 최종 호텔(거리 에 위치)에 멈춰야 하며, 그곳이 목적지이다.
이상적으로는 하루에 200마일을 여행하고 싶지만, 호텔 간격에 따라 불가능할 수도 있다. 하루 동안 마일을 여행하면, 그날의 **벌점(penalty)**은 이다. 당신은 총 벌점을 최소화하도록 여행을 계획하고 싶다. 즉, 모든 여행 일수에 대한 일일 벌점의 합을 최소화해야 한다. 멈출 최적의 호텔 순서를 결정하는 효율적인 알고리즘을 제시하시오.
6.3. Yuckdonald's는 Quaint Valley Highway(QVH)를 따라 일련의 레스토랑을 개점하는 것을 고려하고 있다. 개의 가능한 위치는 직선상에 있으며, QVH 시작점으로부터의 거리는 마일 단위로 증가하는 순서로 이다. 제약 조건은 다음과 같다:
- 각 위치에서 Yuckdonald's는 최대 하나의 레스토랑을 개점할 수 있다. 위치 에 레스토랑을 개점할 때 예상되는 이익은 이며, 이고 이다.
- 두 레스토랑은 최소 마일 떨어져 있어야 하며, 는 양의 정수이다.
주어진 제약 조건 하에서 최대 예상 총 이익을 계산하는 효율적인 알고리즘을 제시하시오.
6.4. 당신은 개의 문자 로 구성된 문자열을 가지고 있는데, 모든 구두점이 사라진 손상된 텍스트 문서("itwasthebestoftimes...")라고 생각한다. 당신은 **사전(dictionary)**을 사용하여 문서를 재구성하고 싶다. 사전은 부울 함수 dict(.) 형태로 제공된다: 어떤 문자열 에 대해,
(a) 문자열 이 유효한 단어들의 시퀀스로 재구성될 수 있는지 여부를 결정하는 동적 프로그래밍(dynamic programming) 알고리즘을 제시하시오. dict 호출이 단위 시간을 소요한다고 가정할 때, 실행 시간은 최대 이어야 한다. (b) 문자열이 유효한 경우, 해당 단어 시퀀스를 출력하도록 알고리즘을 만드시오.
6.5. 체커보드 페블링. 4개의 행과 개의 열을 가진 체커보드가 주어지며, 각 칸에는 정수가 쓰여 있다. 또한 개의 조약돌(pebble) 세트가 주어지며, 이 중 일부 또는 전부를 체커보드에 놓아(각 조약돌은 정확히 한 칸에 놓을 수 있음) 조약돌로 덮인 칸의 정수 합을 최대화하고자 한다. 한 가지 제약 조건이 있다: 조약돌 배치가 **유효(legal)**하려면, 두 조약돌이 수평 또는 수직으로 인접한 칸에 있을 수 없다(대각선 인접은 허용된다). (a) 어떤 열에서 발생할 수 있는 **유효한 패턴(legal patterns)**의 수를 결정하고(인접 열의 조약돌을 무시하고 독립적으로) 이 패턴들을 설명하시오.
두 패턴이 인접한 열에 배치되어 유효한 배치를 형성할 수 있다면 **호환 가능(compatible)**하다고 하자. 첫 개 열 으로 구성된 부분 문제들을 고려하자. 각 부분 문제는 마지막 열에 나타나는 패턴인 **유형(type)**을 할당받을 수 있다. (b) 호환성과 유형의 개념을 사용하여, 최적의 배치를 계산하는 시간 동적 프로그래밍 알고리즘을 제시하시오.
6.6. 세 기호 에 대한 곱셈 연산을 다음 표에 따라 정의하자; 따라서 등이다. 표에 정의된 곱셈 연산은 **결합 법칙(associative)**도 **교환 법칙(commutative)**도 성립하지 않음에 유의하라.
와 같은 기호 문자열을 검사하여, 결과 표현식의 값이 가 되도록 문자열에 괄호를 묶는 것이 가능한지 여부를 결정하는 효율적인 알고리즘을 찾으시오. 예를 들어, 입력 에 대해 알고리즘은 이므로 '예'를 반환해야 한다.
6.7. 회문(palindromic) 부분 수열은 왼쪽에서 오른쪽으로 읽거나 오른쪽에서 왼쪽으로 읽거나 동일한 부분 수열이다. 예를 들어, 다음 시퀀스는
와 를 포함하여 많은 회문 부분 수열을 가지고 있다(반면에 부분 수열 는 회문이 아니다). 시퀀스 를 입력으로 받아 가장 긴 회문 부분 수열의 길이를 반환하는 알고리즘을 고안하시오. 실행 시간은 이어야 한다.
6.8. 두 문자열 와 가 주어졌을 때, 우리는 **가장 긴 공통 부분 문자열(longest common substring)**의 길이를 찾고자 한다. 즉, 를 만족하는 인덱스 와 가 존재하는 가장 큰 를 찾는 것이다. 이를 시간에 수행하는 방법을 보이시오.
6.9. 특정 문자열 처리 언어는 문자열을 두 조각으로 분할하는 기본 연산을 제공한다. 이 연산은 원본 문자열을 복사하는 것을 포함하므로, 절단 위치에 관계없이 길이가 인 문자열에 대해 단위의 시간이 소요된다. 이제, 문자열을 여러 조각으로 나누고 싶다고 가정하자. 분할이 이루어지는 순서는 총 실행 시간에 영향을 미칠 수 있다. 예를 들어, 20자 문자열을 위치 3과 10에서 자르고 싶을 때, 위치 3에서 먼저 자르면 총 비용은 이 발생하지만, 위치 10에서 먼저 자르면 으로 더 나은 비용이 발생한다.
길이 인 문자열에서 개의 절단 위치가 주어졌을 때, 문자열을 개의 조각으로 분할하는 최소 비용을 찾는 동적 프로그래밍 알고리즘을 제시하시오.
6.10. 앞면 세기. 정수 과 , 그리고 이 주어졌을 때, 개의 편향된 동전을 독립적으로 무작위로 던졌을 때 정확히 개의 앞면이 나올 확률을 결정하고자 한다. 여기서 는 번째 동전이 앞면이 나올 확률이다. 이 task에 대한 알고리즘을 제시하시오. 범위의 두 숫자를 시간에 곱하고 더할 수 있다고 가정한다.
6.11. 두 문자열 와 가 주어졌을 때, 우리는 **가장 긴 공통 부분 수열(longest common subsequence)**의 길이를 찾고자 한다. 즉, 를 만족하는 와 인 인덱스가 존재하는 가장 큰 를 찾는 것이다. 이를 시간에 수행하는 방법을 보이시오.
6.12. 평면상에 개의 꼭짓점(x, y 좌표로 지정됨)을 가진 볼록 다각형(convex polygon) 가 주어진다. 의 **삼각 분할(triangulation)**은 의 개 대각선들의 집합으로, 어떤 두 대각선도 (끝점에서 만나는 경우를 제외하고) 교차하지 않는다. 삼각 분할은 다각형의 내부를 개의 서로 다른 삼각형으로 나눈다. 삼각 분할의 **비용(cost)**은 그 안에 있는 대각선 길이의 합이다. 최소 비용 삼각 분할을 찾는 효율적인 알고리즘을 제시하시오. (힌트: 임의의 꼭짓점에서 시작하여 시계 방향으로 의 꼭짓점에 으로 레이블을 지정하시오. 에 대해, 부분 문제 를 꼭짓점 로 이루어진 다각형의 최소 비용 삼각 분할로 정의하시오.)
6.13. 다음 게임을 고려하시오. "딜러"는 의 "카드" 시퀀스를 앞면이 보이도록 제시하며, 각 카드 는 값 를 가진다. 그런 다음 두 플레이어는 번갈아 가며 시퀀스에서 카드를 한 장씩 가져가지만, (남아있는) 시퀀스의 첫 번째 또는 마지막 카드만 가져갈 수 있다. 목표는 가장 큰 총 가치의 카드를 모으는 것이다. (예를 들어, 카드를 다른 액면가의 지폐로 생각할 수 있다.) 은 짝수라고 가정한다. (a) 첫 번째 플레이어가 사용 가능한 카드 중 더 큰 가치의 카드를 선택하는 것이 최적이 아닌 카드 시퀀스를 보이시오. 즉, 자연스러운 탐욕적 전략(greedy strategy)이 최적이 아님을 보이시오. (b) 첫 번째 플레이어의 최적 전략을 계산하는 알고리즘을 제시하시오. 초기 시퀀스가 주어지면, 알고리즘은 시간에 일부 정보를 미리 계산해야 하며, 그런 다음 첫 번째 플레이어는 미리 계산된 정보를 찾아봄으로써 각 움직임을 시간에 최적으로 수행할 수 있어야 한다.
6.14. 천 자르기. 크기의 직사각형 천 조각이 주어지며, 와 는 양의 정수이다. 또한 천을 사용하여 만들 수 있는 가지 제품 목록이 주어진다. 각 제품 에 대해 크기의 천 조각이 필요하며, 제품의 최종 판매 가격은 임을 알고 있다. 는 모두 양의 정수라고 가정한다. 당신은 어떤 직사각형 천 조각이든 수평 또는 수직으로 두 조각으로 자를 수 있는 기계를 가지고 있다. 크기의 천 조각에 대한 최고의 수익을 결정하는 알고리즘을 설계하시오. 즉, 결과 조각으로 만들어진 제품들이 최대 판매 가격 합계를 제공하도록 천을 자르는 전략을 찾는 것이다. 원하는 경우 주어진 제품을 원하는 만큼 만들거나 전혀 만들지 않아도 된다.
6.15. 두 팀 A와 B가 게임을 먼저 이기는 팀을 가리는 경기를 한다고 가정하자. A와 B는 동등한 실력을 가지고 있으므로, 각 팀은 어떤 특정 게임에서든 50%의 승리 확률을 가진다고 가정할 수 있다. 이미 게임을 플레이했으며, A가 승, B가 승을 거두었다고 가정하자. A가 계속해서 경기를 이길 확률을 계산하는 효율적인 알고리즘을 제시하시오. 예를 들어, 이고 이라면, A가 다음 세 게임 중 어떤 게임이든 이겨야 하므로 A가 경기를 이길 확률은 이다.
6.16. 차고 판매 문제. 주어진 일요일 아침에 개의 차고 판매(garage sales)가 진행 중이다: . 각 차고 판매 에 대해, 당신에게 주는 가치 에 대한 추정치가 있다. 어떤 두 차고 판매에 대해서도 에서 로 이동하는 교통 비용(transportation cost) 에 대한 추정치가 있다. 또한 집과 각 차고 판매 사이를 오가는 비용 와 도 주어진다. 당신은 집에서 시작하여 집으로 돌아오는 주어진 차고 판매의 부분 집합에 대한 **경로(tour)**를 찾아, 총 이익에서 총 교통 비용을 뺀 값을 최대화하고자 한다. 이 문제를 시간에 해결하는 알고리즘을 제시하시오. (힌트: 이 문제는 **외판원 문제(traveling salesman problem)**와 밀접하게 관련되어 있다.)
6.17. 액면가 의 동전을 무제한으로 공급받았을 때, 우리는 값 에 대한 **거스름돈(change)**을 만들고자 한다. 즉, 총 가치가 인 동전 세트를 찾고자 한다. 이것이 불가능할 수도 있다: 예를 들어, 액면가가 5와 10이라면 15에 대한 거스름돈은 만들 수 있지만 12에 대해서는 만들 수 없다. 다음 문제에 대한 동적 프로그래밍 알고리즘을 제시하시오.
6.18. 거스름돈 문제(연습 문제 6.17)의 다음 변형을 고려하시오: 액면가 가 주어지고, 값 에 대한 거스름돈을 만들고 싶지만, 각 액면가는 최대 한 번만 사용할 수 있다. 예를 들어, 액면가가 이라면, 와 에 대한 거스름돈은 만들 수 있지만 40에 대해서는 만들 수 없다(20을 두 번 사용할 수 없기 때문).
입력: 양의 정수 ; 또 다른 정수 . 출력: 각 액면가 를 최대 한 번 사용하여 에 대한 거스름돈을 만들 수 있는가? 이 문제를 시간에 해결하는 방법을 보이시오.
6.19. 거스름돈 문제(연습 문제 6.17)의 또 다른 변형이다.
액면가 의 동전을 무제한으로 공급받았을 때, 우리는 최대 개의 동전을 사용하여 값 에 대한 거스름돈을 만들고자 한다. 즉, 총 가치가 인 개의 동전 세트를 찾고자 한다. 이것이 불가능할 수도 있다: 예를 들어, 액면가가 5와 10이고 이라면, 55에 대한 거스름돈은 만들 수 있지만 65에 대해서는 만들 수 없다. 다음 문제에 대한 효율적인 동적 프로그래밍 알고리즘을 제시하시오.
\begin{aligned} & \text { 입력: } x_{1}, \ldots, x_{n} ; k ; v \text {. } \\ & \text { 질문: 액면가 } x_{1}, \ldots, x_{n} \text>의 동전을 사용하여 최대 } k \text>개의 동전으로 } v \text>에 대한 거스름돈을 만들 수 있는가? } \end{aligned}그림 6.12 프로그래밍 언어 키워드를 위한 두 개의 이진 탐색 트리.
6.20. 최적 이진 탐색 트리(Optimal binary search trees). 특정 언어의 프로그램에서 키워드가 나타나는 빈도를 알고 있다고 가정하자. 예를 들어:
| begin | |
|---|---|
| do | |
| else | |
| end | |
| if | |
| then | |
| while |
우리는 이 키워드들을 **이진 탐색 트리(binary search tree)**로 구성하여, 루트의 키워드가 왼쪽 서브트리의 모든 키워드보다 알파벳 순으로 크고 오른쪽 서브트리의 모든 키워드보다 작도록 하고자 한다(이 규칙은 모든 노드에 적용된다).
그림 6.12의 왼쪽에는 균형 잡힌 예시가 있다. 이 경우, 키워드를 찾을 때 필요한 비교 횟수는 최대 3회이다: 예를 들어, "while"을 찾을 때 "end", "then", "while" 세 노드만 검사된다. 그러나 키워드가 접근되는 빈도를 알고 있으므로, 단어를 찾는 평균 비교 횟수라는 더 세밀한 비용 함수를 사용할 수 있다. 왼쪽 탐색 트리의 경우, 비용은 다음과 같다:
이 측정치에 따르면, 가장 좋은 탐색 트리는 오른쪽의 트리이며, 비용은 2.18이다.
다음 task에 대한 효율적인 알고리즘을 제시하시오. 입력: 개의 단어(정렬된 순서); 이 단어들의 빈도:
출력: 가장 낮은 비용(위에서 정의된 단어를 찾는 예상 비교 횟수)을 가진 이진 탐색 트리.
6.21. 그래프 의 **정점 커버(vertex cover)**는 의 모든 엣지의 적어도 하나의 끝점을 포함하는 정점의 부분 집합 이다. 다음 task에 대한 선형 시간 알고리즘을 제시하시오.
입력: 무방향 트리 .
출력: 의 가장 작은 정점 커버의 크기.
예를 들어, 다음 트리에서 가능한 정점 커버는 와 를 포함하지만 는 아니다. 가장 작은 정점 커버의 크기는 3이다: .
6.22. 다음 task에 대한 알고리즘을 제시하시오.
입력: 개의 양의 정수 리스트; 양의 정수 . 질문: 들의 어떤 부분 집합이 로 합산되는가? (각 는 최대 한 번만 사용할 수 있다.)
6.23. 미션 크리티컬 생산 시스템은 순차적으로 수행되어야 하는 개의 단계를 가지고 있으며; 단계는 기계 에 의해 수행된다. 각 기계 는 신뢰성 있게 작동할 확률 와 고장 날 확률 를 가진다(고장은 독립적이다). 따라서 각 단계를 단일 기계로 구현하면 전체 시스템이 작동할 확률은 이다. 이 확률을 개선하기 위해, 단계를 수행하는 기계 의 개 복사본을 가짐으로써 **중복성(redundancy)**을 추가한다. 개 복사본 모두가 동시에 고장 날 확률은 에 불과하므로, 단계가 올바르게 완료될 확률은 이고 전체 시스템이 작동할 확률은 이다. 각 기계 는 비용 를 가지며, 기계를 구매하기 위한 총 예산 가 있다. (와 는 양의 정수라고 가정한다.) 확률 , 비용 , 그리고 예산 가 주어졌을 때, 사용 가능한 예산 내에서 시스템이 올바르게 작동할 확률을 최대화하는 중복성 을 찾으시오.
6.24. 동적 프로그래밍의 시간 및 공간 복잡도. 길이 과 인 문자열 간의 **편집 거리(edit distance)**를 계산하는 우리의 동적 프로그래밍 알고리즘은 크기의 테이블을 생성하므로 시간과 공간이 필요하다. 실제로는 시간 부족보다 공간 부족이 먼저 발생할 것이다. 이 공간 요구 사항을 어떻게 줄일 수 있는가? (a) 편집 거리의 값만 계산하려는 경우(최적 편집 시퀀스 대신), 어떤 주어진 시간에 테이블의 작은 부분만 유지하면 되므로 공간만 필요함을 보이시오. (b) 이제 최적 편집 시퀀스도 원한다고 가정하자. 이전에 보았듯이, 이 문제는 해당 그리드 형태의 DAG(grid-shaped dag) 문제로 재구성될 수 있으며, 목표는 노드 에서 노드 까지의 최적 경로를 찾는 것이다. 이 공식을 사용하는 것이 편리할 것이며, 편의를 위해 이 2의 거듭제곱이라고 가정할 수도 있다.
편집 거리 알고리즘에 매우 유용할 작은 추가 사항부터 시작하자. DAG의 최적 경로는 어떤 에 대해 중간 노드 를 통과해야 한다; 알고리즘을 수정하여 이 값 도 반환하도록 하는 방법을 보이시오. (c) 이제 재귀적인 방식을 고려하시오:
procedure find-path \(((0,0) \rightarrow(n, m))\)
compute the value \(k\) above
find-path \(((0,0) \rightarrow(k, m / 2))\)
find-path \(((k, m / 2) \rightarrow(n, m))\)
concatenate these two paths, with \(k\) in the middle
이 방식이 시간과 공간에서 실행될 수 있음을 보이시오.
6.25. 다음 **3-분할 문제(3-partition problem)**를 고려하시오. 정수 이 주어졌을 때, 을 세 개의 서로 다른 부분 집합 로 분할하여 다음을 만족하는 것이 가능한지 여부를 결정하고자 한다:
예를 들어, 입력 에 대한 답은 '예'이다. 왜냐하면 분할이 있기 때문이다. 반면에 입력 에 대한 답은 '아니오'이다.
과 에 대해 다항 시간으로 실행되는 3-분할 문제에 대한 동적 프로그래밍 알고리즘을 고안하고 분석하시오.
6.26. 서열 정렬(Sequence alignment). 새로운 유전자가 발견되면, 그 기능을 이해하기 위한 표준적인 접근 방식은 알려진 유전자 데이터베이스를 검색하여 유사한 일치 항목을 찾는 것이다. 두 유전자의 유사성은 정렬되는 정도에 따라 측정된다. 이를 공식화하기 위해, 유전자를 알파벳 에 대한 긴 문자열로 생각해보자. 두 유전자(문자열) 와 를 고려하자. 와 의 정렬은 이 두 문자열을 열로 작성하여 일치시키는 방법이다. 예를 들어:
| - | - | |||||
|---|---|---|---|---|---|---|
| - |
여기서 "-"는 "갭(gap)"을 나타낸다. 각 문자열의 문자는 순서대로 나타나야 하며, 각 열은 적어도 하나의 문자열에서 문자를 포함해야 한다. 정렬의 **점수(score)**는 갭을 수용하기 위한 추가 행과 열을 포함하는 크기 의 스코어링 행렬(scoring matrix) 에 의해 지정된다. 예를 들어, 이전 정렬은 다음 점수를 가진다:
두 문자열 와 및 스코어링 행렬 를 입력으로 받아 가장 높은 점수를 가진 정렬을 반환하는 동적 프로그래밍 알고리즘을 제시하시오. 실행 시간은 이어야 한다.
6.27. 갭 페널티를 사용한 정렬(Alignment with gap penalties). 연습 문제 6.26의 정렬 알고리즘은 서로 유사한 DNA 서열을 식별하는 데 도움이 된다. 이러한 유사한 서열 간의 불일치는 종종 DNA 복제 오류로 인해 발생한다. 그러나 생물학적 복제 과정을 자세히 살펴보면, 이전에 고려했던 스코어링 함수에 질적인 문제가 있음을 알 수 있다: 자연은 한 번에 한 위치만 편집하는 대신 전체 뉴클레오타이드 부분 문자열을 삽입하거나 제거하는 경우가 많다(긴 갭 생성). 따라서 길이 10의 갭에 대한 페널티는 길이 1의 갭에 대한 페널티의 10배가 아니라 훨씬 작아야 한다.
연습 문제 6.26을 반복하되, 이번에는 길이 의 갭에 대한 페널티가 인 수정된 스코어링 함수를 사용하시오. 여기서 와 은 주어진 상수이다(는 보다 크다).
6.28. 국소 서열 정렬(Local sequence alignment). 종종 두 DNA 서열은 상당히 다르지만, 매우 유사하고 고도로 보존된 영역을 포함한다. 두 문자열 와 및 스코어링 행렬 (연습 문제 6.26에서 정의됨)를 입력으로 받아, 모든 부분 문자열 쌍 중에서 가장 높은 점수를 가진 정렬을 가지는 와 의 부분 문자열 와 를 출력하는 알고리즘을 설계하시오. 알고리즘은 시간이 소요되어야 한다.
6.29. 엑손 연결(Exon chaining). 각 유전자는 전체 게놈(DNA 서열)의 하위 영역에 해당하지만, 이 영역의 일부는 "정크 DNA"일 수 있다. 종종 유전자는 **엑손(exons)**이라고 불리는 여러 조각으로 구성되며, 이 조각들은 **인트론(introns)**이라고 불리는 정크 단편에 의해 분리된다. 이는 새로 시퀀싱된 게놈에서 유전자를 식별하는 과정을 복잡하게 만든다. 새로운 DNA 서열이 있고 특정 유전자(문자열)가 그 안에 존재하는지 확인하고 싶다고 가정하자. 유전자가 연속적인 부분 서열일 것이라고 기대할 수 없으므로, 우리는 **부분 일치(partial matches)**를 찾는다. 즉, DNA의 단편들이 유전자에도 존재하는지 확인한다(실제로는 이러한 부분 일치조차도 완벽하지 않고 근사치일 것이다). 그런 다음 이러한 단편들을 조립하려고 시도한다.
를 DNA 서열이라고 하자. 각 부분 일치는 세 개의 값 으로 표현될 수 있다. 여기서 는 단편이고 는 일치의 강도를 나타내는 **가중치(weight)**이다(이는 국소 정렬 점수 또는 다른 통계량일 수 있다). 이러한 잠재적 일치 중 다수는 거짓일 수 있으므로, 목표는 일관성 있는(겹치지 않는) 세 개의 값의 부분 집합을 찾아 총 가중치를 최대화하는 것이다.
이를 효율적으로 수행하는 방법을 보이시오.
6.30. 최대 절약(maximum parsimony)을 통한 진화 트리 재구성. 다양한 종에 걸쳐 특정 유전자를 시퀀싱하는 데 성공했다고 가정하자. 구체적으로, 개의 종이 있고, 서열은 알파벳 에 대한 길이 의 문자열이라고 하자. 이 정보를 사용하여 이 종들의 **진화 역사(evolutionary history)**를 어떻게 재구성할 수 있을까?
진화 역사는 일반적으로 잎이 다른 종들이고, 뿌리가 그들의 공통 조상이며, 내부 가지가 종 분화 사건(speciation events)(즉, 새로운 종이 기존 종에서 분리된 순간)을 나타내는 **트리(tree)**로 표현된다. 따라서 다음을 찾아야 한다:
- 잎에 주어진 종들이 있는 (이진) 진화 트리.
- 각 내부 노드에 대해 길이 의 문자열: 해당 특정 조상의 유전자 서열.
각 노드 에 서열 가 주석으로 달린 가능한 모든 트리 에 대해, 우리는 **절약 원칙(principle of parsimony)**에 기반하여 점수를 할당할 수 있다: 돌연변이가 적을수록 더 가능성이 높다.
가장 높은 점수를 가진 트리를 찾는 것은 어려운 문제이다. 여기서는 그 중 작은 부분만 고려할 것이다: 트리의 구조를 알고 있고, 내부 노드 의 서열 를 채우고 싶다고 가정하자. 다음은 이고 인 예시이다:
 (a) 이 특정 예시에서, 내부 노드 서열의 여러 **최대 절약 재구성(maximum parsimony reconstructions)**이 있다. 그 중 하나를 찾으시오.
(b) 이 task에 대한 효율적인( 과 에 대한) 알고리즘을 제시하시오. (힌트: 서열이 길더라도 한 번에 한 위치씩만 처리할 수 있다.)
(a) 이 특정 예시에서, 내부 노드 서열의 여러 **최대 절약 재구성(maximum parsimony reconstructions)**이 있다. 그 중 하나를 찾으시오.
(b) 이 task에 대한 효율적인( 과 에 대한) 알고리즘을 제시하시오. (힌트: 서열이 길더라도 한 번에 한 위치씩만 처리할 수 있다.)