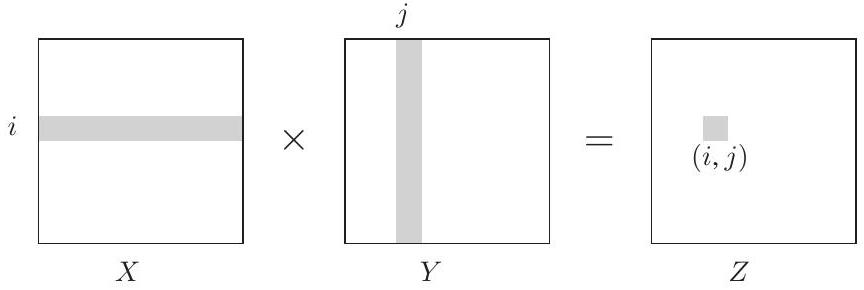
algorithms-part2-4
algorithms-part2-4
algorithms-part2-4
Chapter 2
Divide-and-conquer algorithms
분할 정복(divide-and-conquer) 전략은 다음과 같은 방식으로 문제를 해결한다:
- 문제를 더 작은 동일 유형의 하위 문제(subproblems)로 나눈다.
- 이 하위 문제들을 재귀적으로(recursively) 해결한다.
- 하위 문제들의 답을 적절히 결합한다.
실제 작업은 세 가지 다른 지점에서 조금씩 수행된다: 문제를 하위 문제로 분할하는 과정에서; 재귀의 가장 마지막 단계에서 하위 문제들이 너무 작아져서 즉시 해결될 때; 그리고 부분적인 답들을 하나로 합치는 과정에서. 이 모든 과정은 알고리즘의 핵심적인 재귀 구조에 의해 통합되고 조정된다.
도입 예시로, 이 기법이 우리가 초등학교에서 배운 방법보다 훨씬 더 효율적인 새로운 숫자 곱셈 알고리즘을 어떻게 만들어내는지 살펴볼 것이다.
2.1 Multiplication
수학자 Carl Friedrich Gauss(1777-1855)는 두 복소수의 곱셈
이 네 번의 실수 곱셈을 포함하는 것처럼 보이지만, 실제로는 세 번의 곱셈으로 충분하다는 것을 알아차렸다. 그 이유는 다음과 같다.
우리의 big-O 사고방식에서는 곱셈 횟수를 4회에서 3회로 줄이는 것이 낭비된 독창성처럼 보일 수 있다. 그러나 이 작은 개선은 재귀적으로 적용될 때 매우 중요해진다.
복소수에서 벗어나 이것이 일반적인 곱셈에 어떻게 도움이 되는지 살펴보자. 와 가 두 개의 -비트 정수라고 가정하고, 편의상 이 2의 거듭제곱이라고 가정한다 (더 일반적인 경우는 거의 다르지 않다). 와 를 곱하는 첫 번째 단계로, 각각을 왼쪽 절반과 오른쪽 절반으로 나눈다. 이들은 비트 길이이다.

Carl Friedrich Gauss 1777-1855 (C) Corbis
예를 들어, (아래 첨자 2는 "이진수"를 의미)인 경우 , 이며, 이다. 와 의 곱은 다음과 같이 다시 쓸 수 있다.
우리는 오른쪽 표현식을 통해 를 계산할 것이다. 덧셈은 선형 시간(linear time)이 걸리며, 2의 거듭제곱을 곱하는 것(단순히 왼쪽 시프트)도 마찬가지이다. 중요한 연산은 네 번의 -비트 곱셈인 이다. 이들은 네 번의 재귀 호출로 처리할 수 있다. 따라서 -비트 숫자를 곱하는 우리의 방법은 이 네 쌍의 -비트 숫자를 곱하기 위해 재귀 호출을 수행하는 것으로 시작하고 (크기가 절반인 네 개의 하위 문제), 그 다음 시간에 앞선 표현식을 평가한다. -비트 입력에 대한 전체 실행 시간을 으로 나타내면, 다음과 같은 점화 관계를 얻는다.
이러한 방정식을 푸는 일반적인 전략은 곧 살펴보겠지만, 이 특정 방정식은 로 계산되며, 이는 전통적인 초등학교 곱셈 기법과 동일한 실행 시간이다. 따라서 우리는 근본적으로 새로운 알고리즘을 가지고 있지만, 아직 효율성 면에서는 어떤 진전도 이루지 못했다. 우리의 방법을 어떻게 가속화할 수 있을까?
여기서 Gauss의 트릭이 떠오른다. 에 대한 표현식이 네 번의 -비트 곱셈을 요구하는 것처럼 보이지만, 이전과 마찬가지로 세 번의 곱셈으로 충분하다. 그 이유는 이기 때문이다. 그 결과로
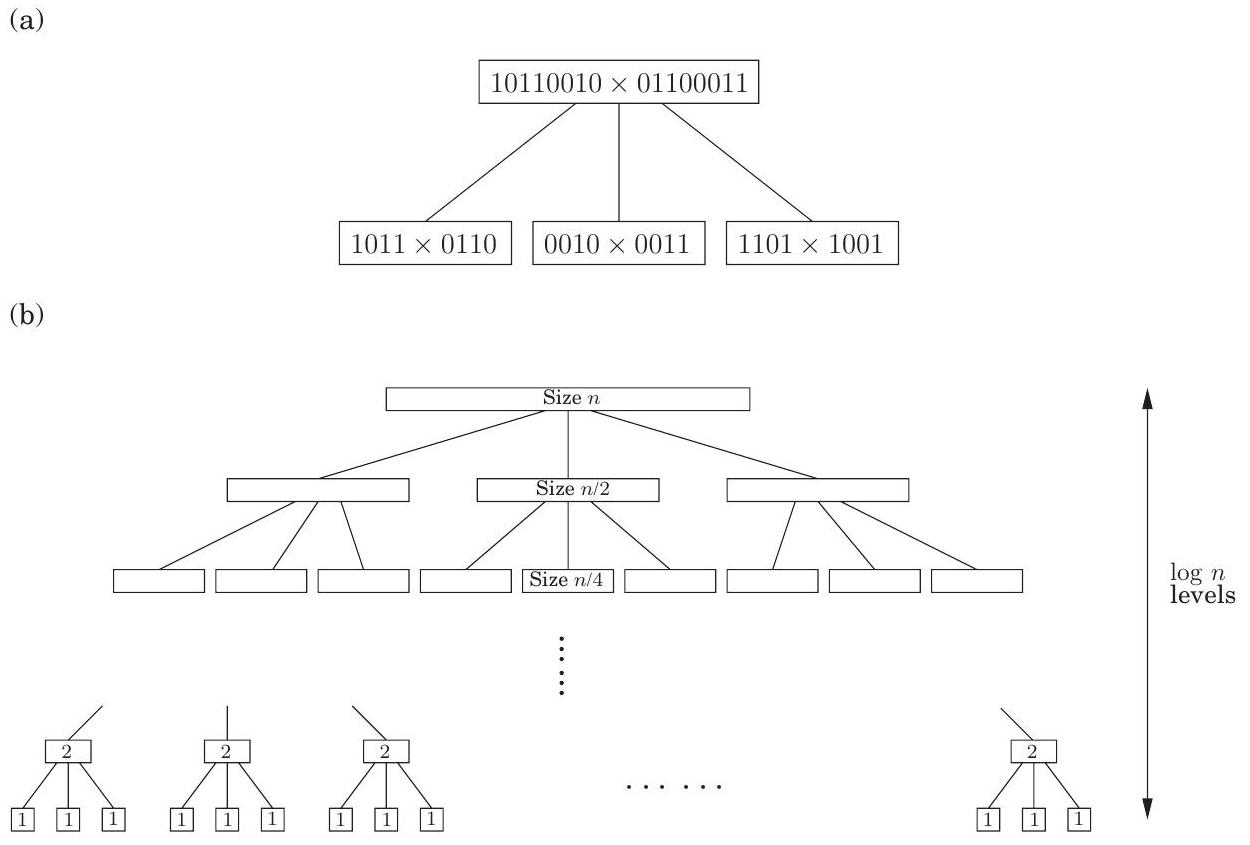
Figure 2.1 정수 곱셈을 위한 분할 정복(divide-and-conquer) 알고리즘.
function multiply( \(x, y\) )
Input: \(n\)-bit positive integers \(x\) and \(y\)
Output: Their product
if \(n=1\) : return xy
\(x_{L}, x_{R}=\) leftmost \(\lceil n / 2\rceil\), rightmost \(\lfloor n / 2\rfloor\) bits of \(x\)
\(y_{L}, y_{R}=\) leftmost \(\lceil n / 2\rceil\), rightmost \(\lfloor n / 2\rfloor\) bits of \(y\)
\(P_{1}=\) multiply \(\left(x_{L}, y_{L}\right)\)
\(P_{2}=\) multiply \(\left(x_{R}, y_{R}\right)\)
\(P_{3}=\) multiply \(\left(x_{L}+x_{R}, y_{L}+y_{R}\right)\)
return \(P_{1} \times 2^{n}+\left(P_{3}-P_{1}-P_{2}\right) \times 2^{n / 2}+P_{2}\)
그림 2.1에 나타난 알고리즘은 개선된 실행 시간을 갖는다.
핵심은 이제 상수 인자 개선, 즉 4에서 3으로의 개선이 재귀의 모든 수준에서 발생하며, 이 복합적인 효과가 라는 극적으로 낮은 시간 경계로 이어진다는 점이다.
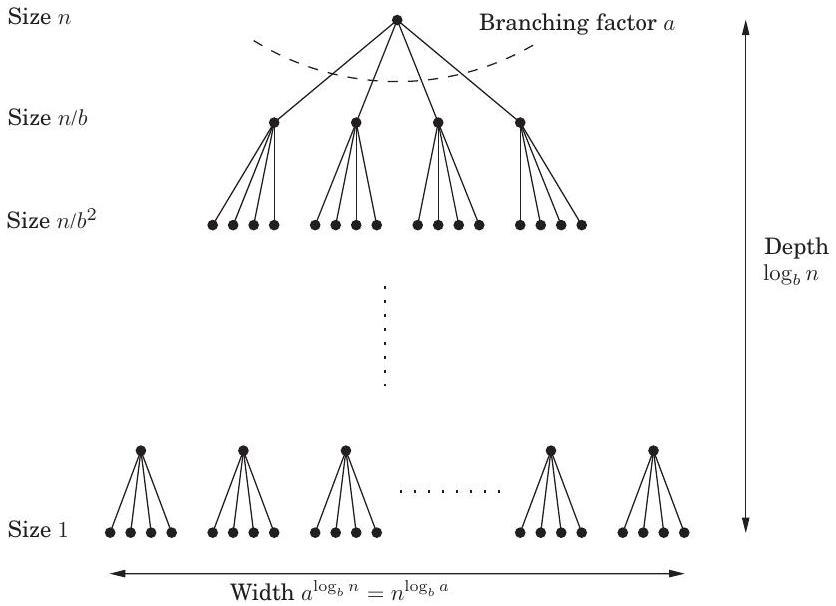
이 실행 시간은 그림 2.2와 같이 트리 구조를 형성하는 알고리즘의 재귀 호출 패턴을 살펴보면 도출할 수 있다. 이 트리의 형태를 이해해 보자. 재귀의 각 연속적인 수준에서 하위 문제의 크기는 절반으로 줄어든다. 수준에서 하위 문제는 크기가 1로 줄어들고, 따라서 재귀가 종료된다. 그러므로 트리의 높이는 이다. 분기 계수는 3이다. 즉, 각 문제는 재귀적으로 세 개의 더 작은 문제를 생성하며, 그 결과 트리의 깊이 에는 개의 하위 문제가 있고, 각 하위 문제의 크기는 이다.
각 하위 문제에 대해 추가 하위 문제를 식별하고 그들의 답을 결합하는 데 선형적인 양의 작업이 수행된다. 따라서 트리의 깊이 에서 소요되는 총 시간은 다음과 같다.
실제로, 점화식은 다음과 같아야 한다.
이는 과 의 길이가 비트일 수 있기 때문이다. 우리가 사용하는 식은 다루기 더 간단하며 정확히 동일한 big-O 실행 시간을 의미한다는 것을 알 수 있다.
Figure 2.2 분할 정복 정수 곱셈. (a) 각 문제는 세 개의 하위 문제로 나뉜다. (b) 재귀의 수준.
가장 상위 수준, 즉 일 때, 이는 으로 계산된다. 가장 하위 수준, 즉 일 때, 이는 이며, 이는 로 다시 쓸 수 있다 (이유를 아는가?). 이 두 끝점 사이에서 수행되는 작업은 에서 까지 기하급수적으로 증가하며, 각 수준마다 배 증가한다. 증가하는 기하급수열의 합은 상수 인자 내에서 단순히 그 수열의 마지막 항과 같다. 이것이 증가의 빠르기이다 (연습 문제 0.2). 따라서 전체 실행 시간은 이며, 이는 약 이다.
Gauss의 트릭이 없었다면, 재귀 트리는 동일한 높이를 가졌겠지만, 분기 계수는 4였을 것이다. 개의 리프가 있었을 것이고, 따라서 실행 시간은 적어도 이만큼이었을 것이다. 분할 정복(divide-and-conquer) 알고리즘에서 하위 문제의 수는 재귀 트리의 분기 계수로 변환된다. 이 계수의 작은 변화는 실행 시간에 큰 영향을 미칠 수 있다.
실용적인 참고: 일반적으로 1비트까지 재귀하는 것은 의미가 없다. 대부분의 프로세서에서 16비트 또는 32비트 곱셈은 단일 연산이므로, 숫자가 이 범위에 도달하면 내장된 프로시저에 넘겨야 한다.
마지막으로, 영원한 질문: 더 나은 방법이 있을까? 섹션 2.6에서 설명할 또 다른 중요한 분할 정복(divide-and-conquer) 알고리즘인 **고속 푸리에 변환(fast Fourier transform)**을 기반으로 하는 훨씬 빠른 숫자 곱셈 알고리즘이 존재한다.
2.2 Recurrence relations
분할 정복(Divide-and-conquer) 알고리즘은 종종 일반적인 패턴을 따른다: 크기 의 문제를 개의 크기 의 하위 문제로 재귀적으로 해결한 다음, 이 해답들을 시간에 결합한다 (여기서 이고, 곱셈 알고리즘에서는 이다). 따라서 이들의 실행 시간은 방정식으로 나타낼 수 있다. 우리는 이 일반적인 재귀식에 대한 **닫힌 형태(closed-form)**의 해를 도출하여, 더 이상 새로운 인스턴스마다 명시적으로 해결할 필요가 없도록 할 것이다.
마스터 정리(Master theorem) 만약 이고, 상수 이라면,
이 단일 정리는 우리가 사용할 대부분의 분할 정복(divide-and-conquer) 절차의 실행 시간을 알려준다.
증명. 주장을 증명하기 위해, 편의상 이 의 거듭제곱이라고 가정하는 것부터 시작하자. 이것은 최종 경계에 어떤 중요한 방식으로도 영향을 미치지 않을 것이다. 결국, 은 의 어떤 거듭제곱으로부터 기껏해야 의 곱셈 인자만큼 떨어져 있으며(연습문제 2.2), 이를 통해 의 반올림 효과를 무시할 수 있다.
다음으로, 하위 문제의 크기가 각 재귀 수준마다 인자만큼 감소하므로, 수준 후에 **기저 사례(base case)**에 도달한다는 점에 주목하자. 이것이 **재귀 트리(recursion tree)**의 높이이다. **분기 인자(branching factor)**는 이므로, 트리의 번째 수준은 각각 크기 인 개의 하위 문제로 구성된다(그림 2.3). 이 수준에서 수행되는 총 작업량은 다음과 같다.
가 0(루트)부터 (리프)까지 진행됨에 따라, 이 숫자들은 비율 를 갖는 **등비수열(geometric series)**을 형성한다. **빅-O 표기법(big-O notation)**으로 이러한 수열의 합을 찾는 것은 쉽고(연습문제 0.2), 세 가지 경우로 나뉜다.
-
비율이 1보다 작은 경우. 이 경우 수열은 감소하며, 그 합은 첫 번째 항인 로 주어진다.
-
비율이 1보다 큰 경우. 수열은 증가하며, 그 합은 마지막 항인 로 주어진다.
-
비율이 정확히 1인 경우. 이 경우 수열의 모든 항은 와 같다.
이러한 경우들은 정리 진술의 세 가지 우발 상황으로 직접 변환된다.
Binary search
궁극적인 분할 정복(divide-and-conquer) 알고리즘은 물론 **이진 탐색(binary search)**이다. 정렬된 순서로 키 를 포함하는 큰 파일에서 키 를 찾기 위해, 우리는 먼저 를 와 비교하고, 그 결과에 따라 파일의 첫 번째 절반인 또는 두 번째 절반인 에 대해 재귀적으로 탐색한다. 이 경우의 **점화식(recurrence)**은 이며, 이는 인 경우이다. **마스터 정리(master theorem)**에 대입하면 익숙한 해인 의 실행 시간을 얻는다.
Figure 2.3 크기 의 각 문제는 크기 의 개 하위 문제로 나뉜다.
2.3 Mergesort
숫자 리스트를 정렬하는 문제는 분할 정복(divide-and-conquer) 전략에 즉시 적용될 수 있다: 리스트를 두 개의 절반으로 나누고, 각 절반을 재귀적으로 정렬한 다음, 두 개의 정렬된 하위 리스트를 병합하는 방식이다.
function mergesort(a[1...n])
Input: An array of numbers a[1...n]
Output: A sorted version of this array
if n>1:
return merge(mergesort(a[1...\lfloorn/2]]),
mergesort(a[\lfloorn/2]+1...n]))
else:
return a
이 알고리즘의 정확성은 올바른 merge 서브루틴이 명시되는 한 자명하다. 만약 두 개의 정렬된 배열 와 이 주어졌을 때, 이들을 단일 정렬된 배열 로 효율적으로 병합하는 방법은 무엇일까? 의 첫 번째 요소는 또는 중 더 작은 값이 된다. 나머지 는 재귀적으로 구성될 수 있다.
function merge(x[1...k], y[1...l])
if k=0: return y[1...l]
if l=0: return x[1...k]
if x[1]\leqy[1]:
return x[1]omerge(x[2...k],y[1...l])
else:
return y[1]omerge(x[1...k],y[2...l])
여기서 는 **연결(concatenation)**을 나타낸다. 이 merge 프로시저는 재귀 호출당 일정한 양의 작업을 수행하며(필요한 배열 공간이 미리 할당되었다고 가정할 때), 총 실행 시간은 이다. 따라서 merge는 선형적이며, mergesort에 의해 소요되는 전체 시간은 다음과 같다.
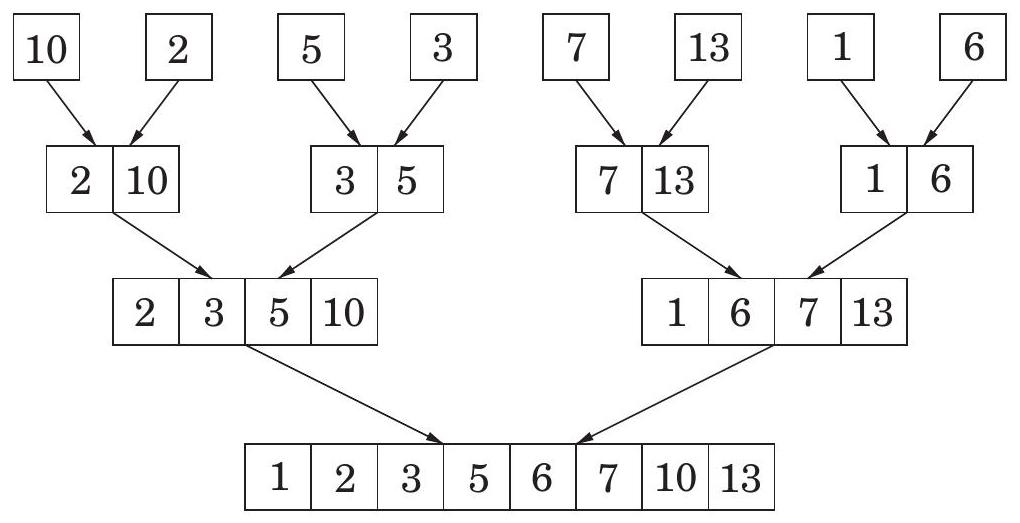
즉, 이다. mergesort 알고리즘을 다시 살펴보면, 모든 실제 작업은 **병합(merging)**에서 이루어지며, 이는 재귀가 단일 요소 배열에 도달할 때까지 시작되지 않는다. 단일 요소들은 쌍으로 병합되어 두 개의 요소를 가진 배열을 생성한다. 그런 다음 이 2-튜플 쌍들이 병합되어 4-튜플을 생성하는 식이다. 그림 2.4는 그 예시를 보여준다.
이러한 관점은 mergesort를 **반복적(iterative)**으로 만드는 방법을 제안하기도 한다. 주어진 순간에 "활성(active)" 배열들의 집합이 있는데, 처음에는 단일 요소들이며, 이들은 쌍으로 병합되어 다음 활성 배열들의 묶음을 생성한다. 이 배열들은 큐에 조직될 수 있으며, 큐의 앞에서 두 배열을 반복적으로 제거하고, 병합한 다음, 결과를 큐의 끝에 넣는 방식으로 처리된다.
다음 의사 코드에서, 기본 연산인 inject는 큐의 끝에 요소를 추가하고, eject는 큐의 앞에서 요소를 제거하고 반환한다.
function iterative-mergesort ( \(a[1 \ldots n]\) )
Input: elements \(a_{1}, a_{2}, \ldots, a_{n}\) to be sorted
\(Q=[]\) (empty queue)
for \(i=1\) to \(n\) :
inject \(\left(Q,\left[a_{i}\right]\right)\)
while \(|Q|>1\) :
inject( \(Q\), merge(eject( \(Q\) ), eject ( \(Q\) )))
return eject( \(Q\) )
Figure 2.4 mergesort의 병합 연산 시퀀스. Input: | 10 | 2 | 5 | 3 | 7 | 13 | 1 | 6 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
Figure 2.4 mergesort의 병합 연산 시퀀스.
An lower bound for sorting
정렬 알고리즘은 트리 형태로 나타낼 수 있다. 다음 그림의 트리는 세 개의 요소 로 구성된 배열을 정렬한다. 이 트리는 과 를 비교하는 것으로 시작하며, 만약 첫 번째 요소가 더 크면 와 비교하고, 그렇지 않으면 와 를 비교한다. 이러한 방식으로 진행하여 결국 리프 노드에 도달하게 되며, 이 리프 노드에는 세 요소의 실제 순서가 1, 2, 3의 permutation으로 표시된다. 예를 들어, 인 경우 "213"으로 레이블된 리프 노드를 얻게 된다.
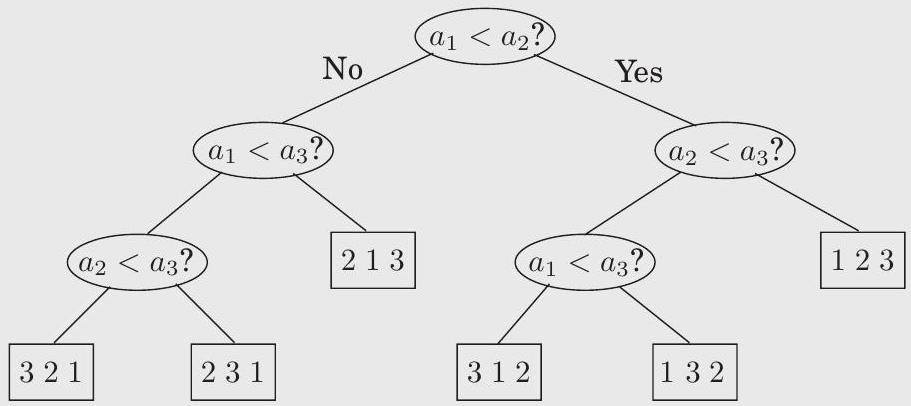
트리의 깊이, 즉 루트에서 리프까지의 가장 긴 경로에 있는 비교 횟수(이 경우 3)는 알고리즘의 **최악의 경우 시간 복잡도(worst-case time complexity)**와 정확히 일치한다.
An lower bound for sorting (continued)
정렬 알고리즘을 이러한 방식으로 살펴보는 것은 mergesort가 최적이라는 것을 주장할 수 있게 해주기 때문에 유용하다. 즉, 개의 요소를 정렬하는 데 번의 비교가 필요하다는 의미에서 말이다.
다음은 그 주장이다: 개의 요소로 구성된 배열을 정렬하는 이러한 트리를 생각해 보자. 각 leaf는 의 순열로 레이블이 지정된다. 사실, 모든 순열은 leaf의 레이블로 나타나야 한다. 그 이유는 간단하다: 만약 특정 순열이 누락되었다면, 이 동일한 순열에 따라 정렬된 입력을 알고리즘에 제공하면 어떻게 될까? 그리고 개의 요소에 대한 순열이 개이므로, 트리는 적어도 개의 leaf를 가져야 한다.
거의 다 왔다: 이것은 이진 트리이며, 우리는 이 트리가 적어도 개의 leaf를 가진다고 주장했다. 이제 깊이 인 이진 트리는 최대 개의 leaf를 가진다는 것을 상기하자(증명: 에 대한 쉬운 귀납법). 따라서 우리 트리의 깊이, 즉 우리 알고리즘의 복잡성은 적어도 이어야 한다.
그리고 (단, )이라는 것은 잘 알려져 있다. 이를 확인하는 방법은 여러 가지가 있다. 가장 쉬운 방법은 임을 알아차리는 것이다. 왜냐하면 에는 보다 큰 인수가 적어도 개 포함되어 있기 때문이다. 그리고 양변에 로그를 취하는 것이다. 다른 방법은 스털링 공식(Stirling's formula)을 상기하는 것이다.
어떤 방법이든, 우리는 개의 요소를 정렬하는 모든 비교 트리는 최악의 경우 번의 비교를 수행해야 하며, 따라서 mergesort가 최적이라는 것을 입증했다! 음, 약간의 세부 사항이 있다: 이 깔끔한 주장은 비교를 사용하는 알고리즘에만 적용된다. 정교한 수치 조작을 사용하여 선형 시간에 작동하는 대체 정렬 전략이 있을 수 있을까? 답은 특정 예외적인 상황에서는 '그렇다'이다. 대표적인 예는 정렬할 요소가 작은 범위 내에 있는 정수일 때이다(연습문제 2.20).
2.4 Medians
숫자 목록의 **중앙값(median)**은 50번째 백분위수이다. 즉, 절반의 숫자는 중앙값보다 크고, 절반은 중앙값보다 작다. 예를 들어, 의 중앙값은 25이다. 이는 숫자를 순서대로 정렬했을 때 중간에 위치하는 요소이기 때문이다. 만약 목록의 길이가 짝수라면, 중간 요소가 될 수 있는 두 가지 선택지가 있는데, 이 경우 우리는 둘 중 더 작은 값을 선택한다.
중앙값의 목적은 일련의 숫자를 단일의 **대표적인 값(typical value)**으로 요약하는 것이다. 평균(mean) 또는 **산술 평균(average)**도 이를 위해 매우 일반적으로 사용되지만, 중앙값은 어떤 의미에서는 데이터에 더 대표적이다. 중앙값은 평균과 달리 항상 데이터 값 중 하나이며, **이상치(outliers)**에 덜 민감하다. 예를 들어, 100개의 1로 이루어진 목록의 중앙값은 (당연히) 1이며, 평균도 마찬가지이다. 그러나 이 숫자들 중 하나가 실수로 10,000으로 손상되면 평균은 100 이상으로 치솟는 반면, 중앙값은 영향을 받지 않는다.
개의 숫자의 중앙값을 계산하는 것은 쉽다. 단순히 정렬하면 된다. 단점은 이 과정이 시간이 걸린다는 것이다. 반면 우리는 이상적으로 선형 시간을 원한다. 우리가 희망을 가질 만한 이유는, 정렬이 실제로 필요한 것보다 훨씬 더 많은 작업을 수행하기 때문이다. 우리는 단지 중간 요소를 원할 뿐이며 나머지 요소들의 상대적인 순서에는 관심이 없다.
재귀적 해결책을 찾을 때, 역설적으로 문제의 더 일반적인 버전을 다루는 것이 종종 더 쉽다. 이는 재귀를 수행할 수 있는 더 강력한 단계를 제공하기 때문이다. 우리의 경우, 우리가 고려할 일반화는 **선택(selection)**이다.
Selection
입력: 숫자 리스트 ; 정수 출력: 의 번째로 작은 원소 예를 들어, 이면 의 최솟값을 찾고, 이면 **중앙값(median)**을 찾는다.
A randomized divide-and-conquer algorithm for selection
다음은 선택(selection)을 위한 분할 정복(divide-and-conquer) 접근 방식이다. 임의의 숫자 에 대해, 리스트 를 세 가지 범주로 나눈다고 상상해 보자: 보다 작은 요소들, 와 같은 요소들(중복이 있을 수 있음), 그리고 보다 큰 요소들. 이들을 각각 이라고 부른다. 예를 들어, 배열
| 2 | 36 | 5 | 21 | 8 | 13 | 11 | 20 | 5 | 4 | 1 | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- | :--- |
이 를 기준으로 분할되면, 생성되는 세 개의 부분 배열은 다음과 같다.
| 2 | 4 | 1 | | :--- | :--- | :--- || 5 | 5 | | :--- | :--- || 36 | 21 | 8 | 13 | 11 | 20 | | :--- | :--- | :--- | :--- | :--- | :--- |.
검색은 이 부분 리스트 중 하나로 즉시 좁혀질 수 있다. 예를 들어, 의 여덟 번째로 작은 요소를 찾고 싶다면, 이므로 의 세 번째로 작은 요소여야 한다는 것을 알 수 있다. 즉, 이다. 더 일반적으로, 를 부분 배열의 크기와 비교함으로써, 원하는 요소가 어느 부분 배열에 있는지 빠르게 결정할 수 있다:
세 개의 부분 리스트 은 로부터 선형 시간(linear time) 안에 계산될 수 있다. 사실, 이 계산은 in place, 즉 새로운 메모리를 할당하지 않고도 수행될 수 있다(연습문제 2.15). 그런 다음 적절한 부분 리스트에 대해 재귀 호출한다. 따라서 분할의 효과는 요소의 수를 에서 로 줄이는 것이다.
선택을 위한 우리의 분할 정복 알고리즘은 이제 를 선택하는 방법에 대한 중요한 세부 사항을 제외하고는 완전히 명시되었다. 는 빠르게 선택되어야 하며, 배열을 상당히 줄여야 한다. 이상적인 상황은 이다. 만약 우리가 항상 이 상황을 보장할 수 있다면, 다음과 같은 실행 시간을 얻을 것이다.
이는 원하는 대로 선형 시간이다. 그러나 이것은 를 **중앙값(median)**으로 선택해야 하는데, 이것이 바로 우리의 궁극적인 목표이다! 대신, 우리는 훨씬 더 간단한 대안을 따른다: 에서 를 무작위로(randomly) 선택한다.
Efficiency analysis
당연히 우리 알고리즘의 실행 시간은 의 무작위 선택에 따라 달라진다. 지속적으로 운이 나빠 를 배열의 가장 큰 요소(또는 가장 작은 요소)로 계속 선택하여 매번 배열을 단 하나의 요소만큼만 축소할 수도 있다. 이전 예시에서는 을 먼저 선택한 다음 을 선택하는 식이다. 이러한 최악의 시나리오는 우리의 선택 알고리즘이 (중앙값을 계산할 때) 다음을 수행하도록 강제할 것이다.
연산을 수행하게 되지만, 이러한 상황이 발생할 가능성은 극히 낮다. 마찬가지로 이전에 논의했던 최상의 시나리오, 즉 무작위로 선택된 각 가 배열을 완벽하게 절반으로 나누어 의 실행 시간을 초래하는 경우도 발생할 가능성이 낮다. 에서 에 이르는 이 스펙트럼에서 평균 실행 시간은 어디에 위치할까? 다행히도 평균 실행 시간은 최상의 경우 시간과 매우 가깝다.
의 운 좋은 선택과 운 나쁜 선택을 구별하기 위해, 가 선택된 배열의 25번째에서 75번째 백분위수 내에 있을 경우 good하다고 부를 것이다. 우리는 이러한 의 선택을 선호하는데, 이는 서브리스트 과 의 크기가 의 4분의 3 이하가 되도록 보장하여 (이유를 알겠는가?) 배열이 상당히 축소되기 때문이다. 다행히도 good한 는 풍부하다: 어떤 리스트의 절반은 25번째에서 75번째 백분위수 사이에 있어야 한다!
무작위로 선택된 가 good할 확률이 50%라고 할 때, good한 를 얻기 위해 평균적으로 몇 개의 를 선택해야 할까? 다음은 더 익숙한 재구성이다 (연습문제 1.34도 참조):
보조정리 평균적으로 공정한 동전은 "앞면"이 나올 때까지 두 번 던져야 한다.
증명. 앞면이 나올 때까지 던져야 하는 예상 횟수를 라고 하자. 우리는 적어도 한 번은 던져야 하며, 만약 앞면이 나오면 끝이다. 만약 뒷면이 나오면 (확률 로 발생), 반복해야 한다. 따라서 가 되며, 이를 계산하면 이다. I
그러므로 평균적으로 두 번의 분할 연산 후에 배열은 크기의 4분의 3 이하로 줄어들 것이다. 크기 의 배열에 대한 예상 실행 시간을 이라고 하면, 다음을 얻는다.
이는 다음 진술의 양변에 기댓값을 취함으로써 얻어진다: 크기 의 배열에서 걸리는 시간
그리고 우변에 대해서는 합의 기댓값은 기댓값의 합이라는 익숙한 속성을 사용한다.
The unix sort command
정렬 및 중앙값 찾기 알고리즘을 비교해 보면, 공통적인 divide-and-conquer 철학과 구조를 넘어 정확히 반대되는 특징을 가지고 있음을 알 수 있다. Mergesort는 배열을 가장 편리한 방식(첫 번째 절반, 두 번째 절반)으로 두 개로 분할하며, 각 절반에 있는 요소들의 크기에는 전혀 신경 쓰지 않는다. 하지만 정렬된 부분 배열들을 합치는 데 많은 노력을 기울인다. 이와 대조적으로, 중앙값 알고리즘은 분할에 신중하며(작은 숫자 먼저, 그 다음 큰 숫자), 재귀 호출로 작업이 끝난다.
Quicksort는 중앙값 알고리즘과 정확히 동일한 방식으로 배열을 분할하는 정렬 알고리즘이다. 두 번의 재귀 호출을 통해 부분 배열들이 정렬되면 더 이상 할 일이 없다. Quicksort의 최악의 경우 성능은 중앙값 찾기와 마찬가지로 이다. 그러나 평균적인 경우 임이 증명될 수 있으며(연습문제 2.24), 경험적으로 다른 정렬 알고리즘보다 뛰어난 성능을 보인다. 이러한 이유로 Quicksort는 많은 애플리케이션에서 선호되는 알고리즘이 되었는데, 예를 들어 매우 큰 파일을 정렬하는 코드의 기반이 된다.
이 재귀 관계로부터 우리는 이라는 결론을 내릴 수 있다. 즉, 어떤 입력에 대해서도 우리 알고리즘은 평균적으로 선형적인 단계 수 후에 올바른 답을 반환한다.
2.5 Matrix multiplication
두 행렬 와 의 곱은 세 번째 행렬 이며, 번째 원소는 다음과 같다.
더 시각적으로 설명하자면, 는 의 번째 행과 의 번째 열의 **내적(dot product)**이다.
일반적으로 는 와 같지 않다. 즉, 행렬 곱셈은 교환법칙이 성립하지 않는다.
위의 공식은 행렬 곱셈에 대한 알고리즘을 의미한다. 계산해야 할 원소가 개이고, 각 원소는 시간이 걸리기 때문이다. 한동안 이것이 가능한 최상의 실행 시간이라고 널리 믿어졌으며, 특정 계산 모델에서는 어떤 알고리즘도 더 나은 성능을 낼 수 없다는 것이 증명되기도 했다. 따라서 1969년 독일 수학자 Volker Strassen이 **분할 정복(divide-and-conquer)**에 기반한 훨씬 더 효율적인 알고리즘을 발표했을 때 큰 반향을 일으켰다.
행렬 곱셈은 **블록 단위(blockwise)**로 수행될 수 있기 때문에 하위 문제로 나누기가 특히 쉽다. 이것이 무엇을 의미하는지 이해하기 위해 를 네 개의 블록으로 나누고, 도 마찬가지로 나눈다.
그러면 이들의 곱은 이 블록들을 사용하여 표현될 수 있으며, 마치 블록들이 단일 원소인 것처럼 정확히 표현된다 (연습문제 2.11).
이제 분할 정복 전략을 갖게 되었다. 크기 의 곱 를 계산하기 위해, 여덟 개의 크기 곱 를 재귀적으로 계산한 다음, 몇 번의 시간 덧셈을 수행한다. 총 실행 시간은 다음 점화식으로 설명된다.
이것은 기본 알고리즘과 동일한 으로, 인상적이지 않은 결과이다. 그러나 효율성은 더욱 향상될 수 있으며, 정수 곱셈과 마찬가지로 핵심은 영리한 대수학에 있다. 놀랍게도 는 단지 일곱 개의 하위 문제로부터 계산될 수 있는데, 그 분해 방식이 너무나 교묘하고 복잡해서 Strassen이 어떻게 이를 발견할 수 있었는지 궁금할 정도이다!
여기서
새로운 실행 시간은 다음과 같다.
이는 **마스터 정리(master theorem)**에 의해 이 된다.
2.6 The fast Fourier transform
지금까지 우리는 **분할 정복(divide-and-conquer)**이 정수와 행렬을 곱하는 빠른 알고리즘을 어떻게 제공하는지 살펴보았다. 다음 목표는 다항식이다. 차수 인 두 다항식의 곱은 차수 인 다항식이 된다. 예를 들어:
더 일반적으로, 이고 일 때, 이들의 곱 의 계수는 다음과 같다.
(인 경우, 와 는 0으로 간주한다.) 이 공식으로 를 계산하는 데는 단계가 필요하며, 모든 개의 계수를 찾는 데는 시간이 소요될 것으로 보인다. 과연 이보다 더 빠르게 다항식을 곱할 수 있을까?
우리가 개발할 **고속 푸리에 변환(fast Fourier transform)**이라는 해법은 신호 처리 분야에 혁명을 일으켰고, 사실상 이 분야를 정의했다(다음 박스 참조). 그 엄청난 중요성과 다양한 연구 분야에서 얻은 풍부한 통찰력 때문에, 우리는 평소보다 좀 더 여유롭게 접근할 것이다. 핵심 알고리즘만 원하는 독자는 2.6.4절로 바로 건너뛸 수 있다.
2.6.1 An alternative representation of polynomials
다항식 곱셈을 위한 빠른 알고리즘을 도출하기 위해 우리는 다항식의 중요한 속성에서 영감을 얻는다.
사실 차 다항식은 개의 서로 다른 점에서 그 값에 의해 고유하게 특징지어진다.
이것의 친숙한 예시는 "두 점은 하나의 직선을 결정한다"는 것이다. 우리는 나중에 더 일반적인 진술이 왜 참인지 알게 될 것이지만(64페이지), 당분간은 이것이 다항식의 대안적인 표현을 제공한다. 서로 다른 점 를 고정하자. 우리는 차 다항식 를 다음 중 하나로 지정할 수 있다:
- 계수
- 값
이 두 가지 표현 중 두 번째가 다항식 곱셈에 더 매력적이다. 곱 는 차이므로, 개의 점에서 그 값에 의해 완전히 결정된다. 그리고 주어진 점 에서의 값은 와 를 곱하는 것만으로도 쉽게 알아낼 수 있다. 따라서 값 표현(value representation)에서 다항식 곱셈은 선형 시간(linear time)이 소요된다.
문제는 입력 다항식과 그 곱이 계수로 지정될 것으로 예상된다는 점이다. 따라서 우리는 먼저 계수에서 값으로 변환해야 한다. 이는 선택된 점에서 다항식을 평가하는 문제일 뿐이다. 그런 다음 값 표현에서 곱셈을 수행하고, 마지막으로 계수로 다시 변환해야 하는데, 이 과정을 **보간(interpolation)**이라고 한다.
 그림 2.5는 결과 알고리즘을 보여준다.
그림 2.5는 결과 알고리즘을 보여준다.
Why multiply polynomials?
우선, 정수 곱셈을 위한 가장 빠른 알고리즘은 다항식 곱셈에 크게 의존한다는 것이 밝혀졌다. 결국, 다항식과 이진 정수는 상당히 유사하다. 변수 를 2진수로 대체하고 올림수(carry)에 주의하면 된다. 그러나 아마도 더 중요한 것은, 다항식 곱셈이 신호 처리에 매우 중요하다는 점이다.
신호는 시간(그림 (a) 참조) 또는 위치의 함수인 모든 양을 의미한다. 예를 들어, 스피커 입 근처의 기압 변동을 측정하여 사람의 목소리를 포착하거나, 각도의 함수로 밝기를 측정하여 밤하늘의 별 패턴을 포착할 수 있다.
 (a)
(a)
 (b)
(b)
 (c)
(c)
신호에서 정보를 추출하려면 먼저 샘플링을 통해 신호를 디지털화한 다음(그림 (b) 참조), 어떤 방식으로든 신호를 변환하는 시스템을 거쳐야 한다. 이 출력은 시스템의 **응답(response)**이라고 불린다:
중요한 시스템 클래스 중 하나는 선형(linear) 시스템(두 신호의 합에 대한 응답은 개별 응답의 합과 같다)과 시불변(time invariant) 시스템(입력 신호를 시간 만큼 이동시키면 동일한 출력이 만큼 이동되어 생성된다)이다. 이러한 속성을 가진 모든 시스템은 가장 간단한 입력 신호인 단위 임펄스(unit impulse) 에 대한 응답으로 완전히 특성화된다. 는 에서만 "급격한 변화(jerk)"를 포함한다(그림 (c) 참조). 이를 이해하기 위해 먼저 라는 밀접한 관련이 있는 **이동된 임펄스(shifted impulse)**를 고려해보자. 이 임펄스에서는 시점에서 급격한 변화가 발생한다. 모든 신호 는 가 시점에서의 동작을 선택하도록 하여 이들의 선형 조합으로 표현될 수 있다.
(신호가 개의 샘플로 구성된 경우). 선형성에 의해, 입력 에 대한 시스템 응답은 다양한 에 대한 응답에 의해 결정된다. 그리고 시불변성에 의해, 이들은 다시 에 대한 응답인 임펄스 응답(impulse response) 의 이동된 복사본에 불과하다.
다시 말해, 시간 에서의 시스템 출력은 다음과 같다.
이는 다항식 곱셈 공식과 정확히 일치한다!
그림 2.5 다항식 곱셈
Input: 차수 \(d\)인 두 다항식 \(A(x)\)와 \(B(x)\)의 계수
Output: 이들의 곱 \(C=A \cdot B\)
Selection
\(n \geq 2 d+1\)인 점 \(x_{0}, x_{1}, \ldots, x_{n-1}\)을 선택한다.
Evaluation
\(A\left(x_{0}\right), A\left(x_{1}\right), \ldots, A\left(x_{n-1}\right)\)와 \(B\left(x_{0}\right), B\left(x_{1}\right), \ldots, B\left(x_{n-1}\right)\)를 계산한다.
Multiplication
모든 \(k=0, \ldots, n-1\)에 대해 \(C\left(x_{k}\right)=A\left(x_{k}\right) B\left(x_{k}\right)\)를 계산한다.
Interpolation
\(C(x)=c_{0}+c_{1} x+\cdots+c_{2 d} x^{2 d}\)를 복구한다.
두 다항식 표현의 등가성은 이 상위 수준 접근 방식이 정확하다는 것을 명확히 보여주지만, 얼마나 효율적일까? 분명히 selection 단계와 번의 multiplication은 전혀 문제가 되지 않으며, 단지 선형 시간(linear time)이 소요된다. (보간(interpolation)은 차치하고, 이에 대해서는 아는 바가 더 적다) evaluation은 어떨까? 차수 인 다항식을 한 점에서 평가하는 데는 단계가 필요하므로(연습문제 2.29), 개 점에 대한 기본 시간은 이다. 이제 우리는 **고속 푸리에 변환(FFT)**이 시간 안에 이를 수행한다는 것을 알게 될 것이다. 이는 의 특히 영리한 선택으로, 개별 점에 필요한 계산이 서로 겹치고 공유될 수 있도록 한다.
2.6.2 Evaluation by divide-and-conquer
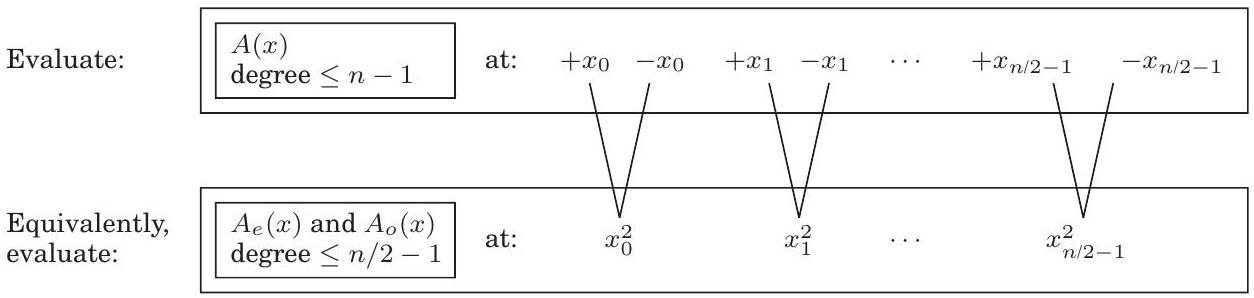
차수 인 다항식 를 평가할 개의 점을 선택하는 방법에 대한 아이디어가 있다. 만약 이 점들을 양-음 쌍으로 선택한다면, 즉,
의 짝수 제곱은 의 짝수 제곱과 일치하기 때문에 각 와 에 필요한 계산이 많이 겹치게 된다.
이를 조사하기 위해 를 홀수 차수와 짝수 차수로 분리해야 한다. 예를 들어,
괄호 안의 항들은 에 대한 다항식임을 주목하자. 더 일반적으로,
여기서 짝수 계수를 갖는 와 홀수 계수를 갖는 는 차수 인 다항식이다 (편의상 이 짝수라고 가정한다). 쌍을 이루는 점 가 주어졌을 때, 계산에 필요한 연산은 계산에 재활용될 수 있다:
다시 말해, 개의 쌍을 이루는 점 에서 를 평가하는 것은 의 절반 차수를 갖는 와 를 단지 개의 점 에서 평가하는 것으로 줄어든다.
크기 의 원래 문제는 이 방식으로 크기 의 두 가지 하위 문제로 재구성되며, 그 다음에는 선형 시간 산술 연산이 따른다. 만약 재귀를 사용할 수 있다면, 실행 시간이
인 분할 정복(divide-and-conquer) 절차를 얻게 될 것이며, 이는 우리가 원하는 이다.
하지만 문제가 있다: 플러스-마이너스 트릭은 재귀의 최상위 레벨에서만 작동한다. 다음 레벨에서 재귀를 수행하려면 개의 평가점 자체가 플러스-마이너스 쌍이어야 한다. 하지만 제곱이 어떻게 음수가 될 수 있을까? 이 작업은 불가능해 보인다! 물론, 복소수를 사용하지 않는 한 말이다.
좋다, 그렇다면 어떤 복소수를 사용해야 할까? 이를 알아내기 위해 과정을 "역설계"해보자. 재귀의 가장 아래쪽에는 단일 점이 있다. 이 점은 1이라고 가정할 수 있으며, 이 경우 그 위의 레벨은 1의 제곱근인 로 구성되어야 한다.
그 다음 레벨은 뿐만 아니라 복소수 를 포함한다. 여기서 는 허수 단위이다. 이 방식으로 계속하면 결국 개의 초기 점 집합에 도달하게 된다. 아마도 당신은 이미 그것이 무엇인지 짐작했을 것이다.
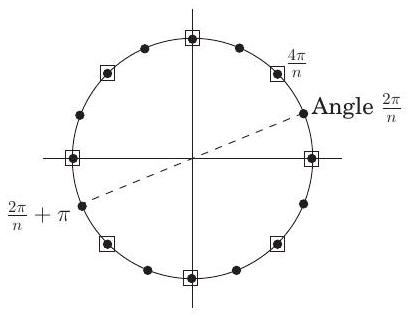
 그것은 바로 복소수 차 단위근(complex nth roots of unity), 즉 방정식 의 개의 복소수 해이다.
그것은 바로 복소수 차 단위근(complex nth roots of unity), 즉 방정식 의 개의 복소수 해이다.
그림 2.6은 복소수에 대한 몇 가지 기본 사실을 그림으로 보여준다. 이 그림의 세 번째 패널은 차 단위근을 소개한다: 복소수 이며, 여기서 이다. 만약 이 짝수라면,
- 차 단위근은 플러스-마이너스 쌍을 이룬다: .
- 이들을 제곱하면 차 단위근이 생성된다.
따라서 이 2의 거듭제곱인 경우 이 숫자들로 시작하면, 재귀의 연속적인 레벨에서 에 대해 차 단위근을 갖게 될 것이다. 이 모든 숫자 집합은 플러스-마이너스 쌍을 이루므로, 마지막 패널에 표시된 것처럼 우리의 **분할 정복(divide-and-conquer)**은 완벽하게 작동한다. 결과 알고리즘은 **고속 푸리에 변환(fast Fourier transform)**이다 (그림 2.7).
2.6.3 Interpolation
현재 상황을 정리해 보자. 우리는 먼저 다항식을 계수(coefficients)로 표현하는 방식과 선택된 점들의 집합에서 값(values)으로 표현하는 두 가지 방식이 있다는 관찰을 기반으로, 다항식 곱셈을 위한 상위 수준의 계획을 개발했다(그림 2.5).

값 표현 방식은 다항식 곱셈을 매우 간단하게 만들지만, 전체 알고리즘의 입력과 출력이 계수 표현 방식으로 지정되기 때문에 이를 무시할 수 없다.
그래서 우리는 FFT를 설계했다. 이는 점들 이 복소수 차 단위근 일 때, 계수에서 값으로 시간에 이동하는 방법이다.
그림 2.6 복소수 단위근은 우리의 divide-and-conquer 방식에 이상적이다.
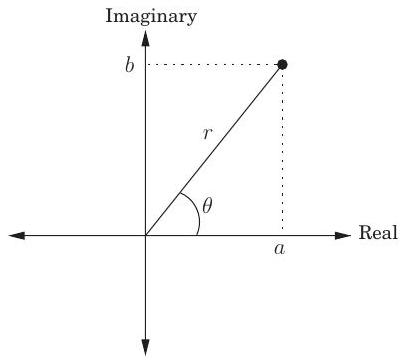 | 복소 평면 <br> 는 위치 에 그려진다. <br> 극좌표: 로 다시 작성되며, 로 표기된다. <br> - 길이 . <br> - 각도 . <br> - 는 항상 를 법으로 하여 줄일 수 있다. <br> 예시: 숫자 -1 <br> 극좌표 |
|---|---|
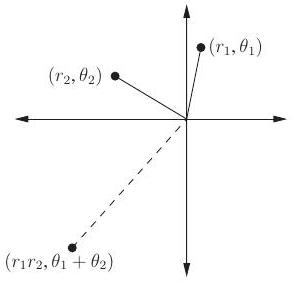 | 극좌표에서 곱셈은 쉽다 <br> 길이를 곱하고 각도를 더한다: <br> . <br> 임의의 에 대해, <br> - (왜냐하면 ). <br> - 만약 가 단위 원 위에 있다면 (즉, ), 이다. |
 | 차 복소수 단위근 <br> 방정식 의 해. <br> 곱셈 규칙에 따라: 해는 이며, 는 의 배수이다 (여기서는 에 대해 표시됨). <br> 이 짝수일 때: <br> - 이 숫자들은 플러스-마이너스 쌍을 이룬다: . <br> - 이들의 제곱은 차 단위근이며, 여기서는 상자로 표시되어 있다. |
| Divide-and-conquer 단계 |
그림 2.7 고속 푸리에 변환 (다항식 공식)
function FFT ( \(A, \omega\) )
Input: 차수가 \(\leq n-1\)인 다항식 \(A(x)\)의 계수 표현, 여기서 \(n\)은 2의 거듭제곱이다.
\(\omega\), \(n\)차 단위근
Output: 값 표현 \(A\left(\omega^{0}\right), \ldots, A\left(\omega^{n-1}\right)\)
if \(\omega=1\) : return \(A(1)\)
\(A(x)\)를 \(A_{e}\left(x^{2}\right)+x A_{o}\left(x^{2}\right)\) 형태로 표현한다.
FFT ( \(A_{e}, \omega^{2}\) )를 호출하여 \(\omega\)의 짝수 거듭제곱에서 \(A_{e}\)를 평가한다.
FFT \(\left(A_{o}, \omega^{2}\right)\)를 호출하여 \(\omega\)의 짝수 거듭제곱에서 \(A_{o}\)를 평가한다.
for \(j=0\) to \(n-1\) :
\(A\left(\omega^{j}\right)=A_{e}\left(\omega^{2 j}\right)+\omega^{j} A_{o}\left(\omega^{2 j}\right)\)를 계산한다.
return \(A\left(\omega^{0}\right), \ldots, A\left(\omega^{n-1}\right)\)
남아있는 마지막 퍼즐 조각은 역 연산인 **보간(interpolation)**이다. 놀랍게도 다음과 같은 사실이 밝혀질 것이다.
따라서 보간은 우리가 바랄 수 있는 가장 간단하고 우아한 방식으로 해결된다. 즉, 동일한 FFT 알고리즘을 사용하되, 대신 를 사용하여 호출하는 것이다! 이것은 기적적인 우연처럼 보일 수 있지만, 다항식 연산을 선형 대수의 언어로 다시 표현하면 훨씬 더 합리적으로 이해될 것이다. 그동안 우리의 다항식 곱셈 알고리즘(그림 2.5)은 이제 완전히 명시되었다.
A matrix reformulation
interpolation을 더 명확하게 이해하기 위해, 차수가 인 다항식 에 대한 두 가지 표현 사이의 관계를 명시적으로 설정해 보자. 이들은 모두 개의 숫자로 이루어진 벡터이며, 하나는 다른 하나의 선형 변환이다:
가운데 행렬을 이라고 부르자. 이 행렬의 특수한 형식인 Vandermonde matrix는 많은 놀라운 속성을 가지며, 그중 다음 속성은 우리에게 특히 중요하다.
만약 가 서로 다른 숫자라면, 은 invertible하다.
의 존재는 앞선 행렬 방정식을 역변환하여 계수를 값으로 표현할 수 있게 해준다. 요약하자면,
Evaluation은 을 곱하는 것이고, interpolation은 를 곱하는 것이다. 다항식 연산에 대한 이러한 재구성은 그 본질을 더욱 명확하게 드러낸다. 무엇보다도, 이는 우리가 계속해서 가정해 왔던, 가 임의의 개 지점에서의 값으로 고유하게 특징지어진다는 가정을 마침내 정당화한다. 사실, 우리는 이제 이러한 상황에서 의 계수를 제공하는 명시적인 공식을 갖게 되었다. Vandermonde matrix는 또한 일반적인 행렬보다 더 빠르게 invert할 수 있다는 특징이 있다. 시간 대신 시간에 가능하다. 그러나 이를 interpolation에 사용하는 것은 여전히 우리에게 충분히 빠르지 않으므로, 우리는 다시 특별히 선택한 지점인 complex roots of unity로 눈을 돌린다.
Interpolation resolved
선형대수학적 관점에서, FFT는 우리가 **계수 표현(coefficient representation)**이라고 부르는 임의의 차원 벡터에 행렬을 곱하는 연산이다.
여기서 는 복소수 차 **단위근(root of unity)**이며, 은 2의 거듭제곱이다. 이 행렬이 얼마나 간단하게 설명되는지 주목하라: 번째 원소(행과 열의 인덱스를 0부터 시작)는 이다.
를 곱하는 것은 번째 좌표축(위치 에 1이 있고 나머지는 모두 0인 벡터)을 의 번째 열로 매핑한다. 이제 중요한 관찰이 있는데, 곧 증명할 것이다: 의 열들은 서로 직교한다(orthogonal). 따라서 이 열들은 **푸리에 기저(Fourier basis)**라고 불리는 대안적인 좌표계의 축으로 생각할 수 있다. 벡터에 을 곱하는 효과는 벡터를 표준 기저(일반적인 축 집합)에서 의 열로 정의되는 푸리에 기저로 회전시키는 것이다(Figure 2.8). 따라서 **FFT는 기저 변환(change of basis), 즉 강체 회전(rigid rotation)**이다. 의 역행렬은 푸리에 기저에서 표준 기저로 되돌아가는 반대 회전이다. 직교 조건을 정확하게 작성하면 이 역변환을 쉽게 파악할 수 있다.
역변환 공식 .
그러나 또한 차 단위근이므로, 보간(interpolation)—또는 동등하게 를 곱하는 것—은 가 로 대체된 FFT 연산 자체이다.
이제 자세히 살펴보자. 편의상 를 으로 두고, 의 열들을 의 벡터로 생각해보자. 에서 두 벡터 와 사이의 각도는 그들의 **내적(inner product)**에 스케일링 인자를 곱한 값이다.
Figure 2.8 FFT는 표준 좌표계(여기서는 로 표시된 축)의 점들을 가져와 푸리에 기저(여기서는 로 표시된 의 열들)로 회전시킨다. 예를 들어, 방향의 점들은 방향으로 매핑된다.
여기서 는 의 **복소 켤레(complex conjugate)**를 나타낸다. 이 값은 벡터들이 같은 방향에 있을 때 최대가 되고, 서로 직교할 때 0이 된다.
우리가 필요한 근본적인 관찰은 다음과 같다. 보조정리(Lemma) 행렬 의 열들은 서로 직교한다. 증명. 행렬 의 임의의 열 와 열 의 내적을 취하면 다음과 같다.
이것은 첫 항이 1이고, 마지막 항이 이며, 공비가 인 **등비수열(geometric series)**이다. 따라서 이 값은 로 평가되며, 이는 인 경우를 제외하고는 0이다. 인 경우에는 모든 항이 1이 되고 합은 이 된다.
직교성은 단일 방정식으로 요약될 수 있다.
이는 가 의 번째 열과 번째 열의 내적이기 때문이다. (이유를 알겠는가?) 이는 즉시 를 의미한다. 우리는 역변환 공식을 얻었다! 하지만 이것이 우리가 이전에 주장했던 것과 같은 공식일까? 살펴보자. 의 번째 원소는 의 해당 원소의 복소 켤레, 즉 이다. 따라서 이며, 증명이 완료된다.
이제 우리는 마침내 한 걸음 물러서서 전체 과정을 기하학적으로 볼 수 있다. 우리가 수행해야 할 **다항식 곱셈(polynomial multiplication)**이라는 task는 표준 기저보다 푸리에 기저에서 훨씬 쉽다. 따라서 우리는 먼저 벡터를 푸리에 기저로 회전시킨 다음(평가(evaluation)), task를 수행하고(곱셈(multiplication)), 마지막으로 다시 회전시킨다(보간(interpolation)). 초기 벡터는 **계수 표현(coefficient representations)**이고, 회전된 벡터는 **값 표현(value representations)**이다. 이들 사이를 효율적으로 앞뒤로 전환하는 것이 FFT의 영역이다.
2.6.4 A closer look at the fast Fourier transform
이제 다항식 곱셈을 위한 효율적인 방식이 완전히 구현되었으므로, 이 모든 것을 가능하게 하는 핵심 서브루틴인 **고속 푸리에 변환(fast Fourier transform)**에 대해 더 자세히 살펴보자.
The definitive FFT algorithm
FFT는 입력으로 벡터 와 복소수 를 받는데, 이 의 거듭제곱 은 복소수 차 단위근이다. FFT는 벡터 에 행렬 를 곱하는데, 이 행렬의 번째 원소(행과 열 카운트는 0부터 시작)는 이다. 이 행렬-벡터 곱셈에서 divide-and-conquer를 사용할 가능성은 의 열을 짝수와 홀수로 분리할 때 명확해진다:

두 번째 단계에서는 과 을 사용하여 행렬의 아래쪽 절반에 있는 원소들을 단순화했다. 왼쪽 위 부분 행렬이 이고, 왼쪽 아래 부분 행렬도 마찬가지임을 알 수 있다. 그리고 오른쪽 위와 오른쪽 아래 부분 행렬은 와 거의 동일하지만, 각각 번째 행에 와 가 곱해져 있다. 따라서 최종 결과는 다음 벡터이다.
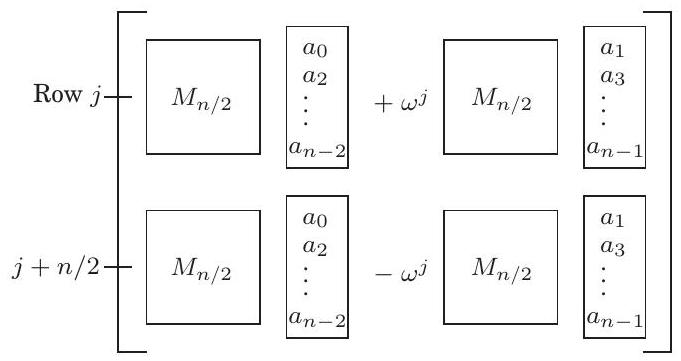
요약하자면, 크기 문제인 와 벡터 의 곱은 두 개의 크기 문제로 표현될 수 있다: 와 의 곱, 그리고 와 의 곱이다. 이 divide-and-conquer 전략은 그림 2.9의 FFT 알고리즘으로 이어지며, 이 알고리즘의 실행 시간은 이다.
Figure 2.9 고속 푸리에 변환
function \(\operatorname{FFT}(a, \omega)\)
Input: An array \(a=\left(a_{0}, a_{1}, \ldots, a_{n-1}\right)\), for \(n\) a power of 2
A primitive \(n\)th root of unity, \(\omega\)
Output: \(M_{n}(\omega) a\)
if \(\omega=1\) : return \(a\)
\(\left(s_{0}, s_{1}, \ldots, s_{n / 2-1}\right)=\operatorname{FFT}\left(\left(a_{0}, a_{2}, \ldots, a_{n-2}\right), \omega^{2}\right)\)
\(\left(s_{0}^{\prime}, s_{1}^{\prime}, s_{n / 2-1}^{\prime}\right)=\operatorname{FFT}\left(\left(a_{1}, a_{3}, \ldots, a_{n-1}\right), \omega^{2}\right)\)
for \(j=0\) to \(n / 2-1\) :
\(r_{j}=s_{j}+\omega^{j} s_{j}^{\prime}\)
\(r_{j+n / 2}=s_{j}-\omega^{j} s_{j}^{\prime}\)
return \(\left(r_{0}, r_{1}, \ldots, r_{n-1}\right)\)
The fast Fourier transform unraveled
지금까지의 모든 논의에서 **고속 푸리에 변환(fast Fourier transform, FFT)**은 분할 정복(divide-and-conquer) 형식 내에 단단히 갇혀 있었다. 이제 그 구조를 완전히 드러내기 위해 재귀를 풀어보자.
FFT의 분할 정복 단계는 매우 간단한 회로로 그릴 수 있다. 다음은 크기 의 문제가 크기 의 두 하위 문제로 축소되는 방식이다 (명확성을 위해 하나의 출력 쌍 ()이 강조되어 있다):
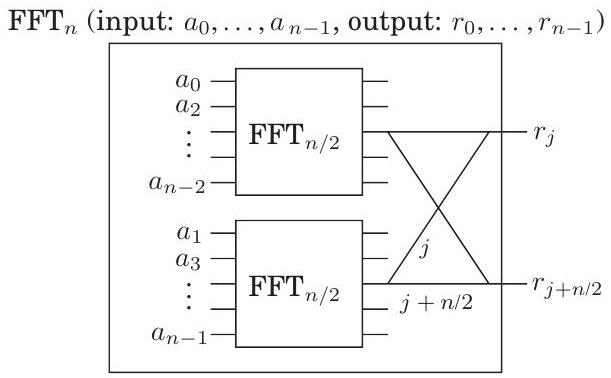
우리는 특정 약어를 사용하고 있다: **가장자리(edge)**는 왼쪽에서 오른쪽으로 복소수를 전달하는 **와이어(wire)**이다. 의 **가중치(weight)**는 "이 와이어의 숫자에 를 곱하라"는 의미이다. 그리고 두 와이어가 왼쪽에서 한 **접합점(junction)**으로 들어오면, 그들이 전달하는 숫자들은 합산된다. 따라서 묘사된 두 출력은 FFT 알고리즘(그림 2.9)에서 다음 명령을 실행한다:
이는 **버터플라이(butterfly)**라고 알려진 와이어 패턴 을 통해 이루어진다. 요소에 대해 FFT 회로를 완전히 풀면 그림 2.10을 얻는다. 다음 사항에 주목하라.
- 개의 입력에 대해 개의 레벨이 있으며, 각 레벨에는 개의 노드가 있어 총 개의 연산이 수행된다.
- 입력은 이라는 특이한 순서로 배열되어 있다.
왜 그럴까? 재귀의 최상위 레벨에서 우리는 먼저 입력의 짝수 계수를 가져온 다음 홀수 계수로 넘어간다는 것을 상기하라. 그런 다음 다음 레벨에서는 이 첫 번째 그룹의 짝수 계수(따라서 4의 배수이거나, 동등하게, 두 개의 최하위 비트가 0인)가 가져와지고, 이런 식으로 계속된다. 다르게 말하면, 입력은 인덱스의 이진 표현의 마지막 비트가 증가하는 순서로 배열되며, 동점일 경우 다음으로 더 중요한 비트를 확인한다. 결과적으로 이진 순서는 이며, 이는 자연적인 순서인 과 동일하지만 비트가 **미러링(mirrored)**되어 있다! 3. 각 입력 와 각 출력 사이에는 고유한 경로가 존재한다.
이 경로는 와 의 이진 표현을 사용하여 가장 쉽게 설명할 수 있다(그림 2.10 참조). 각 노드에서 두 개의 **가장자리(edge)**가 나오는데, 하나는 위로 가는 (0-edge) 가장자리이고
그림 2.10 고속 푸리에 변환 회로.
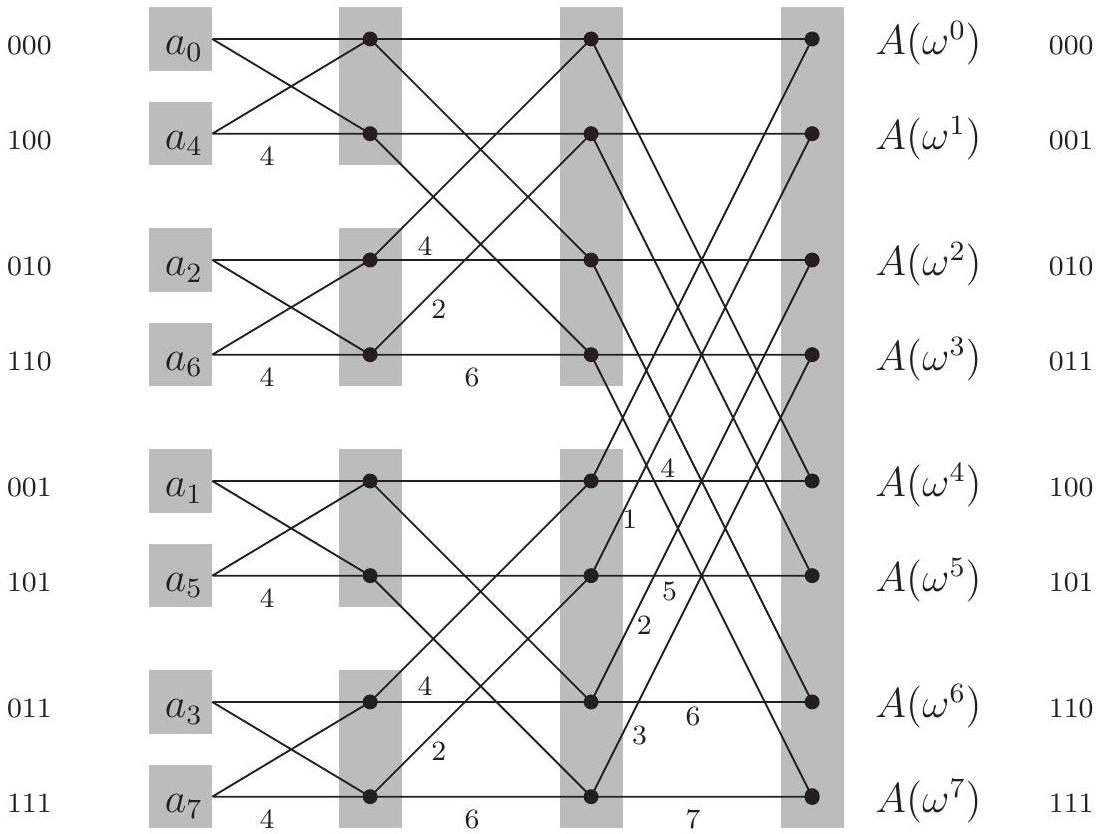
다른 하나는 아래로 가는 (1-edge) 가장자리이다. 어떤 입력 노드에서 로 가려면, 의 비트 표현에 지정된 가장자리를 가장 오른쪽 비트부터 따라가면 된다. (유사하게 역방향 경로를 지정할 수 있는가?) 4. 와 사이의 경로에서 **레이블(label)**은 로 합산된다.
이므로, 이는 출력 에 대한 입력 의 기여가 임을 의미하며, 따라서 회로는 다항식 의 값을 올바르게 계산한다. 5. 마지막으로, FFT 회로는 **병렬 계산(parallel computation)**과 **하드웨어 직접 구현(direct implementation in hardware)**에 적합하다는 점에 주목하라.
The slow spread of a fast algorithm
1963년, 케네디 대통령의 과학 자문 회의에서 프린스턴의 수학자 John Tukey는 IBM의 Dick Garwin에게 **푸리에 변환(Fourier transforms)**을 계산하는 빠른 방법을 설명했다. Garwin은 당시 지진 데이터를 통해 핵폭발을 감지하는 방법을 연구하고 있었고, 푸리에 변환이 그의 방법에서 병목 현상이었기 때문에 주의 깊게 들었다. IBM으로 돌아온 그는 John Cooley에게 Tukey의 알고리즘을 구현해달라고 요청했고, 그들은 이 아이디어가 특허화되지 않도록 논문을 발표하기로 결정했다.
Tukey는 이 주제에 대해 논문을 쓰는 것을 별로 좋아하지 않았기 때문에 Cooley가 주도권을 잡았다. 그리고 이렇게 해서 1965년에 Cooley와 Tukey가 공동 저술한 가장 유명하고 가장 많이 인용된 과학 논문 중 하나가 출판되었다. Tukey가 **FFT(Fast Fourier Transform)**를 발표하기를 꺼려했던 이유는 비밀주의나 특허를 통한 이윤 추구가 아니었다. 그는 이것이 이미 알려져 있을 법한 단순한 관찰이라고 생각했을 뿐이다. 이것은 그 시대의 전형적인 모습이었다. 당시(그리고 한동안 그 이후에도) 알고리즘은 깊이와 우아함이 결여된 2류 수학적 대상으로 간주되어 진지한 주목을 받을 가치가 없다고 여겨졌다.
그러나 Tukey는 한 가지에 대해서는 옳았다. 나중에 밝혀진 바에 따르면, 영국 엔지니어들은 1930년대 후반에 수동 계산을 위해 FFT를 사용했다. 그리고 이 장을 시작했던 위대한 수학자로 마무리하자면, 1800년대 초 **가우스(Gauss)**의 (무엇에 대한?) **보간법(interpolation)**에 관한 논문에는 본질적으로 동일한 아이디어가 담겨 있었다! 가우스의 논문이 오랫동안 비밀로 남아 있었던 것은 구식 암호화 기술로 보호되었기 때문이다. 즉, 그 시대의 대부분의 과학 논문처럼 라틴어로 작성되었기 때문이다.
Exercises
2.1. divide-and-conquer 정수 곱셈 알고리즘을 사용하여 두 이진 정수 10011011과 10111010을 곱하시오. 2.2. 임의의 양의 정수 과 임의의 밑 에 대해, 범위 안에 의 거듭제곱이 존재함을 보이시오. 2.3. 섹션 2.2에서는 **재귀 트리(recursion tree)**를 분석하고 각 레벨에서 수행되는 작업에 대한 공식을 도출하는 재귀 관계 해결 방법을 설명한다. 또 다른 (밀접하게 관련된) 방법은 패턴이 나타날 때까지 재귀를 몇 번 확장하는 것이다. 예를 들어, 익숙한 부터 시작해보자. 을 어떤 상수 에 대해 으로 생각하면 다음과 같다: . 이 규칙을 반복적으로 적용하여 을 , 그 다음 , 그 다음 등으로 제한할 수 있으며, 각 단계에서 우리가 아는 값, 즉 에 더 가까워진다.
패턴이 나타나고 있다. . . 일반항은 다음과 같다.
을 대입하면 을 얻는다. (a) 재귀 관계 에 대해 동일한 작업을 수행하시오. 이 경우 일반적인 번째 항은 무엇인가? 그리고 답을 얻기 위해 어떤 값을 대입해야 하는가? (b) 이제 **마스터 정리(master theorem)**로 다룰 수 없는 경우인 재귀 관계 를 시도해보시오. 이것도 풀 수 있는가? 2.4. 다음 세 가지 알고리즘 중에서 선택한다고 가정해보자:
- 알고리즘 A는 문제를 절반 크기의 다섯 가지 하위 문제로 나누고, 각 하위 문제를 재귀적으로 해결한 다음, 선형 시간으로 해를 결합하여 문제를 해결한다.
- 알고리즘 B는 크기 의 문제를 크기 의 두 가지 하위 문제를 재귀적으로 해결한 다음, 상수 시간으로 해를 결합하여 문제를 해결한다.
- 알고리즘 C는 크기 의 문제를 크기 의 아홉 가지 하위 문제로 나누고, 각 하위 문제를 재귀적으로 해결한 다음, 시간으로 해를 결합하여 문제를 해결한다.
각 알고리즘의 실행 시간(빅-O 표기법)은 얼마이며, 어떤 알고리즘을 선택하겠는가?
2.5. 다음 재귀 관계를 풀고 각각에 대해 경계를 제시하시오.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h) (여기서 은 상수)
(i) (여기서 은 어떤 상수)
(j)
(k)
2.6. 선형 시불변 시스템은 다음과 같은 **임펄스 응답(impulse response)**을 갖는다:
 (a) 이 시스템의 효과를 말로 설명하시오.
(b) 해당 다항식은 무엇인가?
2.7. **차 단위근(nth roots of unity)**의 합은 무엇인가? 이 홀수일 때 그 곱은 무엇인가? 이 짝수일 때는 무엇인가?
2.8. 고속 푸리에 변환(fast Fourier transform, FFT) 연습.
(a) 의 FFT는 무엇인가? 이 경우 적절한 값은 무엇인가? 그리고 은 어떤 시퀀스의 FFT인가?
(b) 에 대해 반복하시오.
2.9. FFT를 이용한 다항식 곱셈 연습.
(a) FFT를 사용하여 두 다항식 과 을 곱하고 싶다고 가정해보자. 적절한 2의 거듭제곱을 선택하고, 두 시퀀스의 FFT를 찾고, 결과를 요소별로 곱한 다음, 역 FFT를 계산하여 최종 결과를 얻으시오.
(b) 다항식 쌍 와 에 대해 반복하시오.
2.10. 값을 갖는 유일한 4차 다항식을 찾으시오. 답을 계수 표현으로 작성하시오.
2.11. 행렬 곱셈 알고리즘(섹션 2.5)을 정당화하면서, 우리는 다음과 같은 블록별 속성을 주장했다: 와 가 행렬이고,
(a) 이 시스템의 효과를 말로 설명하시오.
(b) 해당 다항식은 무엇인가?
2.7. **차 단위근(nth roots of unity)**의 합은 무엇인가? 이 홀수일 때 그 곱은 무엇인가? 이 짝수일 때는 무엇인가?
2.8. 고속 푸리에 변환(fast Fourier transform, FFT) 연습.
(a) 의 FFT는 무엇인가? 이 경우 적절한 값은 무엇인가? 그리고 은 어떤 시퀀스의 FFT인가?
(b) 에 대해 반복하시오.
2.9. FFT를 이용한 다항식 곱셈 연습.
(a) FFT를 사용하여 두 다항식 과 을 곱하고 싶다고 가정해보자. 적절한 2의 거듭제곱을 선택하고, 두 시퀀스의 FFT를 찾고, 결과를 요소별로 곱한 다음, 역 FFT를 계산하여 최종 결과를 얻으시오.
(b) 다항식 쌍 와 에 대해 반복하시오.
2.10. 값을 갖는 유일한 4차 다항식을 찾으시오. 답을 계수 표현으로 작성하시오.
2.11. 행렬 곱셈 알고리즘(섹션 2.5)을 정당화하면서, 우리는 다음과 같은 블록별 속성을 주장했다: 와 가 행렬이고,
여기서 는 부분 행렬일 때, 곱 는 이 블록들로 표현될 수 있다:
이 속성을 증명하시오. 2.12. 다음 프로그램은 의 함수( 형식)로 몇 줄을 출력하는가? 재귀 관계를 작성하고 푸시오. 은 2의 거듭제곱이라고 가정할 수 있다.
function f(n)
if n > 1:
print_line("still going")
f(n/2)
f (n/2)
2.13. **이진 트리(binary tree)**는 모든 정점이 자식이 없거나 두 개의 자식을 가질 때 **완전(full)**하다고 한다. 을 개의 정점을 가진 완전 이진 트리의 수라고 하자. (a) 3, 5, 7개의 정점을 가진 모든 완전 이진 트리를 그려서 의 정확한 값을 결정하시오. 왜 와 같은 짝수 개의 정점은 제외했는가? (b) 일반적인 에 대해 에 대한 재귀 관계를 도출하시오. (c) 귀납법으로 이 임을 보이시오. 2.14. 개의 요소로 구성된 배열이 주어졌을 때, 일부 요소가 중복되어 배열에 두 번 이상 나타나는 것을 발견했다. 배열에서 모든 중복을 시간에 제거하는 방법을 보이시오. 2.15. 중앙값 찾기 알고리즘(섹션 2.4)에서 기본 원시 연산은 분할(split) 연산이다. 이 연산은 배열 와 값 를 입력으로 받아 를 세 가지 집합으로 나눈다: 보다 작은 요소, 와 같은 요소, 보다 큰 요소. 이 분할 연산을 **제자리(in place)**에서, 즉 새로운 메모리를 할당하지 않고 구현하는 방법을 보이시오. 2.16. 첫 개의 셀에 정렬된 정수가 포함되어 있고 나머지 셀은 로 채워진 무한 배열 이 주어졌다. 의 값은 주어지지 않는다. 정수 를 입력으로 받아, 그러한 위치가 존재한다면 배열에서 를 포함하는 위치를 시간에 찾는 알고리즘을 설명하시오. (배열 의 길이가 무한하다는 사실이 불편하다면, 대신 길이가 이지만 이 길이를 알지 못하고, 프로그래밍 언어의 배열 데이터 타입 구현이 인 요소 에 접근할 때마다 오류 메시지 를 반환한다고 가정하시오.) 2.17. 서로 다른 정수로 정렬된 배열 이 주어졌을 때, 인 인덱스 가 있는지 알아내고 싶다. 시간에 실행되는 분할 정복(divide-and-conquer) 알고리즘을 제시하시오. 2.18. 주어진 요소 에 대해 정렬된 배열 을 검색하는 작업을 고려해보자: 이 작업은 일반적으로 **이진 탐색(binary search)**으로 시간에 수행한다. 배열에 비교를 통해서만 접근하는(즉, " 인가?"와 같은 질문을 하는) 모든 알고리즘은 단계를 거쳐야 함을 보이시오. 2.19. -way 병합(merge) 연산. 각각 개의 요소를 가진 개의 정렬된 배열이 있고, 이들을 개의 요소로 구성된 단일 정렬된 배열로 결합하고 싶다고 가정해보자. (a) 한 가지 전략은 다음과 같다: 섹션 2.3의 병합 절차를 사용하여 처음 두 배열을 병합하고, 그 다음 세 번째 배열을 병합하고, 그 다음 네 번째 배열을 병합하는 식으로 계속한다. 이 알고리즘의 시간 복잡도는 와 의 함수로 얼마인가? (b) 분할 정복을 사용하여 이 문제에 대한 더 효율적인 해결책을 제시하시오. 2.20. 정수 배열 이 시간에 정렬될 수 있음을 보이시오. 여기서
이 작을 경우, 이는 선형 시간이다: 이 경우 하한이 적용되지 않는 이유는 무엇인가? 2.21. 평균(Mean)과 중앙값(median). 통계학에서 가장 기본적인 작업 중 하나는 관측치 집합 을 단일 숫자로 요약하는 것이다. 이 요약 통계량에 대한 두 가지 인기 있는 선택은 다음과 같다:
- 중앙값, 이라고 부르겠다.
- 평균, 라고 부르겠다. (a) 중앙값이 함수
를 최소화하는 값임을 보이시오. 간단히 하기 위해 이 홀수라고 가정할 수 있다. (힌트: 인 경우, 를 약간 왼쪽이나 오른쪽으로 이동하면 함수가 감소함을 보이시오.) (b) 평균이 함수
를 최소화하는 값임을 보이시오. 이를 수행하는 한 가지 방법은 미적분학을 사용하는 것이다. 또 다른 방법은 임의의 에 대해 다음을 증명하는 것이다.
에 대한 함수가 에 대한 함수보다 에서 멀리 떨어진 점에 훨씬 더 큰 페널티를 부과하는 방식에 주목하시오. 따라서 는 모든 관측치에 더 가깝게 다가가려고 훨씬 더 노력한다. 이것은 어떤 면에서는 좋은 것처럼 들릴 수 있지만, 몇몇 **이상치(outlier)**만으로도 의 추정치를 심각하게 왜곡할 수 있기 때문에 통계적으로 바람직하지 않다. 따라서 이 보다 더 강건한(robust) 추정량이라고 말하기도 한다. 그러나 이들보다 더 나쁜 것은 함수
를 최소화하는 값이다. (c) 가 시간에 계산될 수 있음을 보이시오 (숫자 가 기본 산술 연산에 단위 시간이 걸릴 만큼 충분히 작다고 가정). 2.22. 크기 과 의 두 개의 정렬된 리스트가 주어졌다. 두 리스트의 합집합에서 번째로 작은 요소를 계산하는 시간 알고리즘을 제시하시오. 2.23. 배열 은 항목의 절반 이상이 동일할 때 **다수 요소(majority element)**를 갖는다고 한다. 배열이 주어졌을 때, 배열에 다수 요소가 있는지 여부를 효율적인 알고리즘으로 판단하고, 있다면 그 요소를 찾는 것이 목표이다. 배열의 요소는 정수와 같은 정렬된 도메인에서 온 것이 아니므로 " 인가?"와 같은 비교는 있을 수 없다. (배열 요소를 GIF 파일이라고 생각해보자.) 그러나 " 인가?"와 같은 질문에는 상수 시간으로 답할 수 있다. (a) 이 문제를 시간에 해결하는 방법을 보이시오. (힌트: 배열 를 절반 크기의 두 배열 과 로 나눈다. 과 의 다수 요소를 아는 것이 의 다수 요소를 알아내는 데 도움이 되는가? 그렇다면 분할 정복 접근 방식을 사용할 수 있다.) (b) 선형 시간 알고리즘을 제시할 수 있는가? (힌트: 또 다른 분할 정복 접근 방식은 다음과 같다:
- 의 요소들을 임의로 짝지어 개의 쌍을 만든다.
- 각 쌍을 살펴본다: 두 요소가 다르면 둘 다 버린다; 같으면 하나만 남긴다.
이 절차 후에 최대 개의 요소가 남고, 에 다수 요소가 있다면 남은 요소에도 다수 요소가 있음을 보이시오.) 2.24. 56페이지에 퀵 정렬(quicksort) 알고리즘에 대한 높은 수준의 설명이 있다. (a) 퀵 정렬의 **의사 코드(pseudocode)**를 작성하시오. (b) 크기 의 배열에서 최악의 경우 실행 시간이 임을 보이시오. (c) 예상 실행 시간이 재귀 관계
를 만족함을 보이시오. 그런 다음, 이 재귀 관계의 해가 임을 보이시오.
2.25. 섹션 2.1에서 우리는 두 개의 -비트 이진 정수 와 를 시간(여기서 )에 곱하는 알고리즘을 설명했다. 이 절차를 fastmultiply(x, y)라고 부르자.
(a) 십진 정수 (1 뒤에 개의 0이 오는 숫자)을 이진수로 변환하고 싶다. 다음은 알고리즘이다 (은 2의 거듭제곱이라고 가정):
function pwr2bin(n)
if n=1: return 10102
else:
z=???
return fastmultiply(z,z)
누락된 세부 사항을 채우시오. 그런 다음 알고리즘의 실행 시간에 대한 재귀 관계를 제시하고 재귀 관계를 푸시오. (b) 다음으로, 자리(여기서 은 2의 거듭제곱)의 임의의 십진 정수 를 이진수로 변환하고 싶다. 알고리즘은 다음과 같다:
function dec2bin(x)
if n=1: return binary[x]
else:
split x into two decimal numbers }\mp@subsup{x}{L}{},\mp@subsup{x}{R}{}\mathrm{ with }n/
digits each
return ???
여기서 binary[·]는 모든 한 자리 정수의 이진 표현을 포함하는 벡터이다. 즉, binary[0]=0_2, binary[1]=1_2부터 binary[9]=1001_2까지이다. binary에서 조회하는 데 시간이 걸린다고 가정한다. 누락된 세부 사항을 채우시오. 다시 한번, 알고리즘의 실행 시간에 대한 재귀 관계를 제시하고 푸시오.
2.26. F. Lake 교수는 -비트 정수를 제곱하는 것이 두 개의 -비트 정수를 곱하는 것보다 점근적으로 빠르다고 학생들에게 말한다. 학생들은 그를 믿어야 하는가?
2.27. 행렬 의 **제곱(square)**은 자신과의 곱, 이다.
(a) 행렬의 제곱을 계산하는 데 다섯 번의 곱셈으로 충분함을 보이시오.
(b) 행렬의 제곱을 계산하는 다음 알고리즘에 무엇이 잘못되었는가?
"Strassen의 알고리즘과 같이 분할 정복 접근 방식을 사용하지만, 크기 의 7개 하위 문제 대신 (a) 부분 덕분에 이제 크기 의 5개 하위 문제를 얻는다. Strassen의 알고리즘과 동일한 분석을 사용하여 알고리즘이 시간에 실행된다고 결론 내릴 수 있다." (c) 사실, 행렬을 제곱하는 것은 행렬 곱셈보다 쉽지 않다. 행렬이 시간에 제곱될 수 있다면, 임의의 두 행렬이 시간에 곱해질 수 있음을 보이시오. 2.28. 아다마르 행렬(Hadamard matrices) 는 다음과 같이 정의된다:
- 는 행렬 [1]이다.
- 인 경우, 는 행렬이다.
길이 인 열 벡터 가 주어졌을 때, 행렬-벡터 곱 가 연산을 사용하여 계산될 수 있음을 보이시오. 관련된 모든 숫자가 덧셈 및 곱셈과 같은 기본 산술 연산에 단위 시간이 걸릴 만큼 충분히 작다고 가정한다. 2.29. 다항식 을 점 에서 평가하고 싶다고 가정해보자. (a) **호너의 규칙(Horner's rule)**으로 알려진 다음 간단한 루틴이 작업을 수행하고 답을 에 남김을 보이시오.
(b) 이 루틴은 의 함수로 몇 번의 덧셈과 곱셈을 사용하는가? 대체 방법이 훨씬 더 나은 다항식을 찾을 수 있는가? 2.30. 이 문제는 **모듈러 산술(modular arithmetic)**에서, 예를 들어 모듈로 7에서 **푸리에 변환(Fourier Transform, FT)**을 수행하는 방법을 보여준다. (a) 모든 거듭제곱 이 서로 다른(모듈로 7) 숫자 가 있다. 이 를 찾고, 임을 보이시오. (흥미롭게도, 모든 소수 모듈로에 대해 그러한 숫자가 존재한다.) (b) FT의 행렬 형식을 사용하여 시퀀스 의 변환을 모듈로 7로 생성하시오; 즉, 이 벡터에 이전에 찾은 값에 대한 행렬 를 곱하시오. 행렬 곱셈에서 모든 계산은 모듈로 7로 수행되어야 한다. (c) 역 FT를 수행하는 데 필요한 행렬을 작성하시오. 이 행렬을 곱하면 원래 시퀀스가 반환됨을 보이시오. (다시 모든 산술은 모듈로 7로 수행되어야 한다.) (d) 이제 FT 모듈로 7을 사용하여 다항식 과 을 곱하는 방법을 보이시오. 2.31. 섹션 1.2.3에서 우리는 두 양의 정수의 **최대 공약수(greatest common divisor, gcd)**를 계산하는 **유클리드 알고리즘(Euclid's algorithm)**을 연구했다: 두 정수를 모두 나누는 가장 큰 정수. 여기서는 분할 정복에 기반한 대체 알고리즘을 살펴볼 것이다. (a) 다음 규칙이 참임을 보이시오.
(b) 최대 공약수를 위한 효율적인 분할 정복 알고리즘을 제시하시오. (c) 와 가 -비트 정수일 때 알고리즘의 효율성이 유클리드 알고리즘과 어떻게 비교되는가? (특히, 이 클 수 있으므로 덧셈과 같은 기본 산술 연산에 상수 시간이 걸린다고 가정할 수 없다.) 2.32. 이 문제에서는 다음 기하학적 작업을 위한 분할 정복 알고리즘을 개발할 것이다.
가장 가까운 쌍(Closest pair) 입력: 평면상의 점 집합, 출력: 가장 가까운 점 쌍: 즉, 와 사이의 거리, 즉
가 최소화되는 쌍. 간단히 하기 위해 은 2의 거듭제곱이고, 모든 -좌표 는 서로 다르며, -좌표도 서로 다르다고 가정한다.
다음은 알고리즘에 대한 높은 수준의 개요이다:
- 정확히 절반의 점이 이고 절반의 점이 인 값을 찾는다. 이를 기반으로 점들을 두 그룹 과 로 나눈다.
- 과 에서 재귀적으로 가장 가까운 쌍을 찾는다. 이 쌍들을 각각 과 이라고 하고, 거리를 각각 과 이라고 하자. 이 두 거리 중 더 작은 것을 라고 하자.
- 의 점과 의 점 사이에 거리 보다 가까운 쌍이 있는지 확인해야 한다. 이를 위해 또는 인 모든 점을 버리고 남은 점들을 좌표로 정렬한다.
- 이제 이 정렬된 리스트를 순회하며 각 점에 대해 리스트에서 다음 일곱 점까지의 거리를 계산한다. 이런 방식으로 찾은 가장 가까운 쌍을 이라고 하자.
- 답은 세 쌍 중 가장 가까운 쌍이다. (a) 이 알고리즘의 정확성을 증명하기 위해 다음 속성을 보이는 것부터 시작하시오: 평면상의 크기의 모든 정사각형은 의 점을 최대 4개 포함한다. (b) 이제 알고리즘이 정확함을 보이시오. 신중하게 고려해야 할 유일한 경우는 가장 가까운 쌍이 과 사이에 분할될 때이다. (c) 알고리즘의 **의사 코드(pseudocode)**를 작성하고, 실행 시간이 재귀 관계:
로 주어진다는 것을 보이시오. 이 재귀 관계의 해가 임을 보이시오. (d) 실행 시간을 으로 줄일 수 있는가? 2.33. 행렬 가 주어졌을 때 인지 확인하고 싶다고 가정해보자. Strassen의 알고리즘을 사용하여 단계로 이를 수행할 수 있다. 이 질문에서는 훨씬 빠른 **무작위 테스트(randomized test)**를 탐구할 것이다. (a) 엔트리가 무작위로 독립적으로 0 또는 1로 선택된(각각 확률 ) -차원 벡터 라고 하자. 이 0이 아닌 행렬일 때, 임을 증명하시오. (b) 일 때 임을 보이시오. 이것이 인지 확인하는 무작위 테스트를 제공하는 이유는 무엇인가? 2.34. 선형 3SAT. 3SAT 문제는 섹션 8.1에 정의되어 있다. 간단히 말해, 입력은 변수 집합에 대한 절(clause) 집합으로 표현된 **부울 공식(Boolean formula)**이며, 목표는 전체 공식이 참으로 평가되도록 하는 이 변수들에 대한 할당(assignment)(참/거짓 값)이 있는지 여부를 결정하는 것이다.
다음과 같은 특별한 지역성(locality) 속성을 가진 3SAT 인스턴스를 고려해보자. 부울 공식에 개의 변수가 있고, 이 변수들이 으로 번호가 매겨져 있으며, 각 절은 서로 이내의 번호를 가진 변수들을 포함한다고 가정한다. 이러한 3SAT 인스턴스를 해결하기 위한 선형 시간 알고리즘을 제시하시오.
Chapter 3
Decompositions of graphs
3.1 Why graphs?
다양한 문제는 그래프의 간결한 그림 언어로 명확하고 정확하게 표현될 수 있다. 예를 들어, 정치 지도를 색칠하는 task를 생각해 보자. 인접한 국가들은 다른 색을 가져야 한다는 명백한 제약 조건 하에, 최소 몇 개의 색이 필요할까? 이 문제를 해결하는 데 있어 한 가지 어려움은 지도 자체가 그림 3.1(a)와 같이 단순화된 버전이라 할지라도, 복잡한 경계, 세 개 이상의 국가가 만나는 국경 초소, 공해, 구불구불한 강 등 관련 없는 정보로 어수선하다는 점이다.
그림 3.1(b)의 수학적 객체인 그래프에는 이러한 방해 요소가 없다. 이 그래프는 각 국가에 대해 하나의 vertex (1은 브라질, 11은 아르헨티나)를 가지며, 인접한 국가들 사이에 edge를 가진다. 이 그래프는 색칠에 필요한 정보만을 정확히 포함하며, 그 이상은 없다. 이제 정확한 목표는 각 vertex에 색을 할당하여 어떤 edge도 같은 색의 끝점을 가지지 않도록 하는 것이다.
그래프 색칠은 지도 디자이너만의 전유물이 아니다. 어떤 대학이 모든 수업에 대한 시험 일정을 잡아야 하고 가능한 한 적은 시간 슬롯을 사용하고 싶다고 가정해 보자. 유일한 제약 조건은 어떤 학생이 두 시험을 모두 수강하는 경우 두 시험을 동시에 배정할 수 없다는 것이다. 이 문제를 그래프로 표현하려면, 각 시험에 대해 하나의 vertex를 사용하고, 충돌이 있는 경우, 즉 어떤 학생이 두 끝점 시험을 모두 수강하는 경우 두 vertex 사이에 edge를 둔다. 각 시간 슬롯을 고유한 색으로 생각하면, 시간 슬롯을 할당하는 것은 이 그래프를 색칠하는 것과 정확히 동일하다!
그래프에 대한 몇 가지 기본 연산은 매우 빈번하게, 그리고 다양한 맥락에서 발생하므로, 이러한 연산에 대한 효율적인 절차를 찾는 데 많은 노력이 기울여졌다. 이 장은 이러한 알고리즘 중 가장 기본적인 것들, 즉 그래프의 기본 연결성 구조를 밝혀내는 알고리즘에 전념한다.
공식적으로, 그래프는 vertex (또는 node) 집합 와 선택된 vertex 쌍 사이의 edge 로 지정된다. 지도 예시에서 이고 는 다른 많은 edge들 중에서 , 그리고 을 포함한다. 여기서 와 사이의 edge는 구체적으로 "가 와 국경을 공유한다"는 것을 의미한다. 이것은 대칭적인
그림 3.1 (a) 지도와 (b) 그 그래프.
관계이다. 즉, 도 와 국경을 공유한다는 것을 의미하며, 우리는 이를 집합 표기법 를 사용하여 나타낸다. 이러한 edge는 **무방향성(undirected)**이며, **무방향성 그래프(undirected graph)**의 일부이다.
때로는 그래프가 이러한 상호성을 가지지 않는 관계를 묘사하기도 하는데, 이 경우 방향이 있는 edge를 사용해야 한다. 에서 로 향하는 방향성 edge (기호로는 ), 또는 에서 로 향하는 edge (기호로는 ), 또는 둘 다 있을 수 있다. 방향성 그래프의 특히 거대한 예시는 월드 와이드 웹의 모든 링크를 나타내는 그래프이다. 이 그래프는 인터넷의 각 사이트에 대해 하나의 vertex를 가지며, 사이트 가 사이트 로의 링크를 가질 때마다 방향성 edge 를 가진다. 총 수십억 개의 node와 edge가 있다! 웹의 가장 기본적인 연결성 속성조차 이해하는 것은 경제적, 사회적으로 큰 관심사이다. 이 문제의 규모는 엄청나지만, 우리는 곧 그래프 구조에 대한 많은 귀중한 정보를 선형 시간(linear time) 내에 결정할 수 있다는 것을 알게 될 것이다.
3.1.1 How is a graph represented?
그래프는 인접 행렬(adjacency matrix)로 표현할 수 있다. 개의 정점 이 있다면, 이는 배열이며, 번째 항목은 다음과 같다:
무방향 그래프(undirected graphs)의 경우, 간선 는 양방향으로 간주될 수 있으므로 행렬은 대칭적이다.
How big is your graph?
인접 행렬(adjacency matrix)과 인접 리스트(adjacency list) 중 어떤 표현이 더 나은가? 이는 그래프의 노드 수인 와 엣지 수인 사이의 관계에 따라 달라진다. 는 만큼 작을 수도 있고(만약 훨씬 작아지면 그래프는 퇴화한다. 예를 들어, 고립된 정점을 갖게 된다), 만큼 클 수도 있다(모든 가능한 엣지가 존재할 때). 가 이 범위의 상한에 가까울 때, 우리는 그 그래프를 dense하다고 부른다. 반대로, 가 에 가까울 때, 그래프는 sparse하다고 한다. 이 장과 다음 두 장에서 보겠지만, 가 이 범위의 어디에 위치하는지는 올바른 그래프 알고리즘을 선택하는 데 중요한 요소가 된다.
마찬가지로, 그래프 표현을 선택하는 데 있어서도 그렇다. 만약 우리가 World Wide Web 그래프를 컴퓨터 메모리에 저장하고자 한다면, 인접 행렬을 사용하기 전에 두 번 생각해야 한다. 이 글을 쓰는 시점에서 검색 엔진은 이 그래프의 약 80억 개의 정점을 알고 있으며, 따라서 인접 행렬은 수천만 테라비트를 차지할 것이다. 다시 이 글을 쓰는 시점에서, 전 세계에 이를 달성할 만큼 충분한 컴퓨터 메모리가 있는지 불분명하다. (그리고 충분한 메모리가 생길 때까지 몇 년을 기다리는 것은 현명하지 않다. 웹은 계속 성장할 것이고 아마 더 빠르게 성장할 것이다.) 인접 리스트를 사용하면 World Wide Web을 표현하는 것이 가능해진다. 웹에는 수십억 개의 하이퍼링크만 존재하며, 각 하이퍼링크는 인접 리스트에서 몇 바이트를 차지할 것이다. 결과물을 저장하는 장치, 즉 1~2테라바이트를 주머니에 넣고 다닐 수 있다 (곧 귀걸이에도 들어갈 수 있겠지만, 그때쯤이면 웹은 더 성장해 있을 것이다).
인접 리스트가 World Wide Web의 경우에 훨씬 더 효과적인 이유는 웹이 매우 sparse하기 때문이다. 평균적인 웹 페이지는 수십억 개의 가능한 페이지 중에서 약 6개 정도의 다른 페이지에만 하이퍼링크를 가지고 있다.
이 형식의 가장 큰 장점은 특정 엣지의 존재 여부를 단 한 번의 메모리 접근으로 **상수 시간(constant time)**에 확인할 수 있다는 것이다. 반면에 행렬은 공간을 차지하며, 그래프에 엣지가 많지 않다면 이는 낭비적이다.
엣지 수에 비례하는 크기를 갖는 대안적인 표현은 **인접 리스트(adjacency list)**이다. 이는 정점당 하나씩, 총 개의 연결 리스트로 구성된다. 정점 에 대한 연결 리스트는 가 나가는 엣지를 갖는 정점, 즉 인 정점 의 이름을 담고 있다. 따라서 그래프가 방향 그래프인 경우 각 엣지는 정확히 하나의 연결 리스트에 나타나고, 무방향 그래프인 경우 두 개의 리스트에 나타난다. 어느 쪽이든, 데이터 구조의 총 크기는 이다. 특정 엣지 의 존재를 확인하는 것은 더 이상 상수 시간이 아니다. 왜냐하면 의 인접 리스트를 훑어봐야 하기 때문이다. 그러나 정점의 모든 이웃을 반복하는 것은 쉽고(해당 연결 리스트를 따라 내려가면서), 곧 보겠지만, 이는 그래프 알고리즘에서 매우 유용한 연산임이 밝혀진다. 다시 말하지만, 무방향 그래프의 경우 이 표현은 일종의 대칭성을 갖는다. 가 의 인접 리스트에 있는 경우에만 가 의 인접 리스트에 있다.
Figure 3.2 그래프를 탐색하는 것은 미로를 탐색하는 것과 다소 비슷하다.
Figure 3.2 그래프를 탐색하는 것은 미로를 탐색하는 것과 다소 비슷하다.
3.2 Depth-first search in undirected graphs
3.2.1 Exploring mazes
**깊이 우선 탐색(Depth-first search)**은 그래프에 대한 풍부한 정보를 드러내는 놀랍도록 다재다능한 선형 시간(linear-time) 절차이다. 이 절차가 다루는 가장 기본적인 질문은 다음과 같다:
주어진 정점에서 그래프의 어떤 부분에 도달할 수 있는가?
이 task를 이해하기 위해, 인접 리스트(adjacency list) 형태로 새로운 그래프를 받은 컴퓨터의 입장이 되어보자. 이 표현은 단 하나의 기본 연산, 즉 정점의 이웃을 찾는 연산만을 제공한다. 이 기본적인 연산만으로는 도달 가능성 문제(reachability problem)가 미로를 탐험하는 것과 매우 유사하다(Figure 3.2). 고정된 장소에서 걷기 시작하여 어떤 교차로(정점)에 도착할 때마다 따라갈 수 있는 다양한 통로(간선)가 있다. 통로를 부주의하게 선택하면 제자리걸음을 하거나 미로의 접근 가능한 부분을 놓칠 수 있다. 분명히 탐색 중에 중간 정보를 기록해야 한다.
이 고전적인 도전은 수세기 동안 사람들을 즐겁게 해왔다. 미로를 탐험하는 데 필요한 것은 실타래와 분필뿐이라는 것을 모두가 알고 있다. 분필은 이미 방문한 교차로를 표시하여 순환(looping)을 방지한다. 실은 항상 시작점으로 돌아가게 하여 이전에 보았지만 아직 조사하지 않은 통로로 돌아갈 수 있게 한다.
컴퓨터에서 이 두 가지 기본 요소인 분필과 실을 어떻게 시뮬레이션할 수 있을까? 분필 표시는 쉽다: 각 정점에 대해 이미 방문했는지 여부를 나타내는 부울 변수를 유지한다. 실타래의 경우, 올바른 사이버 아날로그는 **스택(stack)**이다. 결국, 실의 정확한 역할은 두 가지 기본 연산을 제공하는 것이다. 새로운 교차로에 도달하기 위해 실을 푸는 것(스택의 동등한 연산은 새 정점을 push하는 것)과 이전 교차로로 돌아가기 위해 실을 감는 것(스택을 pop하는 것)이다.
명시적으로 스택을 유지하는 대신, 재귀(recursion)를 통해 암시적으로 스택을 유지할 것이다(재귀는 활성화 레코드(activation records) 스택을 사용하여 구현된다). 결과 알고리즘은 Figure 3.3에 나와 있다.
Figure 3.3 특정 노드에서 도달 가능한 모든 노드 찾기.
procedure explore( \(G, v\) )
Input: \(G=(V, E)\) is a graph; \(v \in V\)
Output: visited(u) is set to true for all nodes \(u\) reachable
from \(v\)
visited(v) = true
previsit(v)
for each edge \((v, u) \in E\) :
if not visited(u): explore(u)
postvisit(v)
previsit 및 postvisit 절차는 선택 사항이며, 정점이 처음 발견될 때와 마지막으로 떠날 때 작업을 수행하기 위한 것이다. 곧 이들의 창의적인 사용법을 보게 될 것이다.
더 즉각적으로, 우리는 explore가 항상 올바르게 작동하는지 확인해야 한다. 이 절차는 노드에서 이웃으로만 이동하므로 에서 도달할 수 없는 영역으로 절대 점프할 수 없기 때문에 너무 멀리 나아가지 않는다. 그러나 에서 도달 가능한 모든 정점을 찾는가? 만약 놓치는 가 있다면, 에서 까지의 경로를 선택하고, 절차가 실제로 방문한 해당 경로의 마지막 정점을 살펴보자. 이 노드를 라고 하고, 같은 경로에서 그 바로 다음 노드를 라고 하자.

따라서 는 방문되었지만 는 방문되지 않았다. 이것은 모순이다. explore 절차가 노드 에 있을 때, 를 알아차리고 로 이동했을 것이기 때문이다.
덧붙여, 이러한 추론 패턴은 그래프 연구에서 자주 발생하며 본질적으로 간소화된 귀납법이다. 더 형식적인 귀납적 증명은 "모든 에 대해, 에서 홉 이내의 모든 노드는 방문된다"와 같은 가설을 설정하는 것으로 시작할 것이다. 는 확실히 방문되므로 기본 사례는 평소와 같이 자명하다. 그리고 일반적인 사례, 즉 홉 떨어진 모든 노드가 방문되면 홉 떨어진 모든 노드도 방문된다는 것을 보여주는 것은 우리가 방금 논의한 것과 정확히 같은 요점이다.
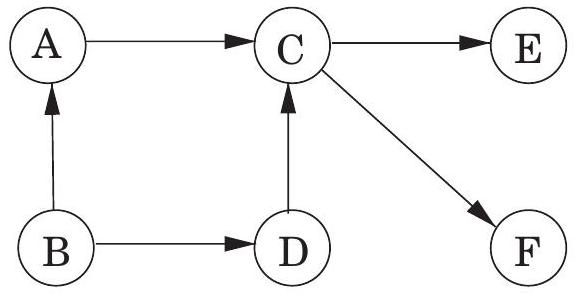
Figure 3.4는 노드 에서 시작하여 방문할 노드를 선택할 때 알파벳 순서로 우선순위를 두어 이전 예시 그래프에서 explore를 실행한 결과를 보여준다. 실선 간선은 실제로 탐색된 간선으로, 각각 explore 호출에 의해 유도되어 새로운 정점의 발견으로 이어졌다.
Figure 3.4 Figure 3.2의 그래프에서 explore 를 실행한 결과.
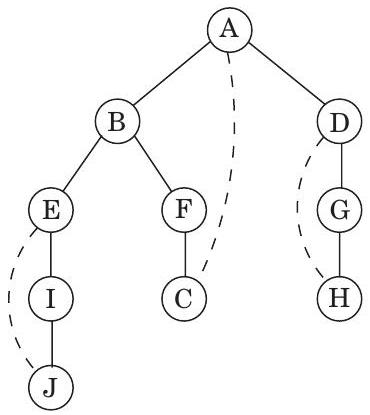
예를 들어, 가 방문되는 동안 간선 가 감지되었고, 가 아직 알려지지 않았기 때문에 explore(E) 호출을 통해 탐색되었다. 이 실선 간선들은 트리(tree)(사이클이 없는 연결된 그래프)를 형성하므로 **트리 간선(tree edges)**이라고 불린다. 점선 간선은 이미 방문한 정점, 즉 익숙한 영역으로 돌아갔기 때문에 무시되었다. 이들은 **역방향 간선(back edges)**이라고 불린다.
3.2.2 Depth-first search
explore 절차는 시작 지점에서 도달할 수 있는 그래프의 일부만 방문한다. 그래프의 나머지 부분을 검사하려면 아직 방문하지 않은 정점에서 절차를 다시 시작해야 한다. 그림 3.5의 알고리즘은 **깊이 우선 탐색(DFS)**이라고 불리며, 전체 그래프가 탐색될 때까지 이 과정을 반복한다.
그림 3.5 깊이 우선 탐색.
procedure dfs(G)
for all v\inV:
visited(v) = false
for all v\inV:
if not visited(v): explore(v)
DFS의 실행 시간을 분석하는 첫 번째 단계는 visited 배열(분필 표시) 덕분에 각 정점이 한 번만 explore된다는 점을 관찰하는 것이다. 정점을 탐색하는 동안 다음 단계가 수행된다:
- 방문한 지점을 표시하고, pre/postvisit을 수행하는 등 고정된 양의 작업.
- 인접한 간선들을 스캔하여 새로운 곳으로 이어지는지 확인하는 루프.
이 루프는 각 정점마다 다른 시간이 소요되므로, 모든 정점을 함께 고려해 보자. 1단계에서 수행되는 총 작업량은 이다. 2단계에서는 전체 DFS 과정에서 각 간선 가 정확히 두 번 검사된다. 한 번은 explore() 중에, 다른 한 번은 explore() 중에 검사된다. 따라서 2단계의 전체 시간은 이며, 깊이 우선 탐색의 실행 시간은 로, 입력 크기에 비례한다. 이는 인접 리스트를 읽는 데만도 이 정도 시간이 걸리기 때문에, 우리가 기대할 수 있는 가장 효율적인 수준이다.
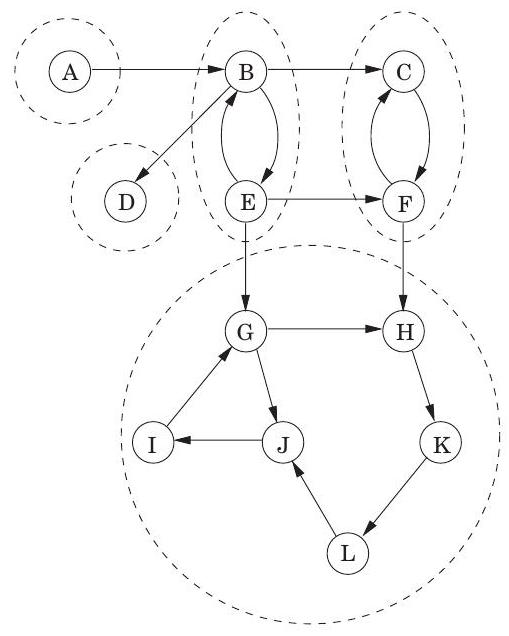
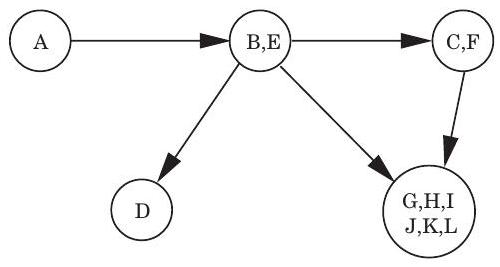
그림 3.6 (a) 12개 노드 그래프. (b) DFS 탐색 포레스트.
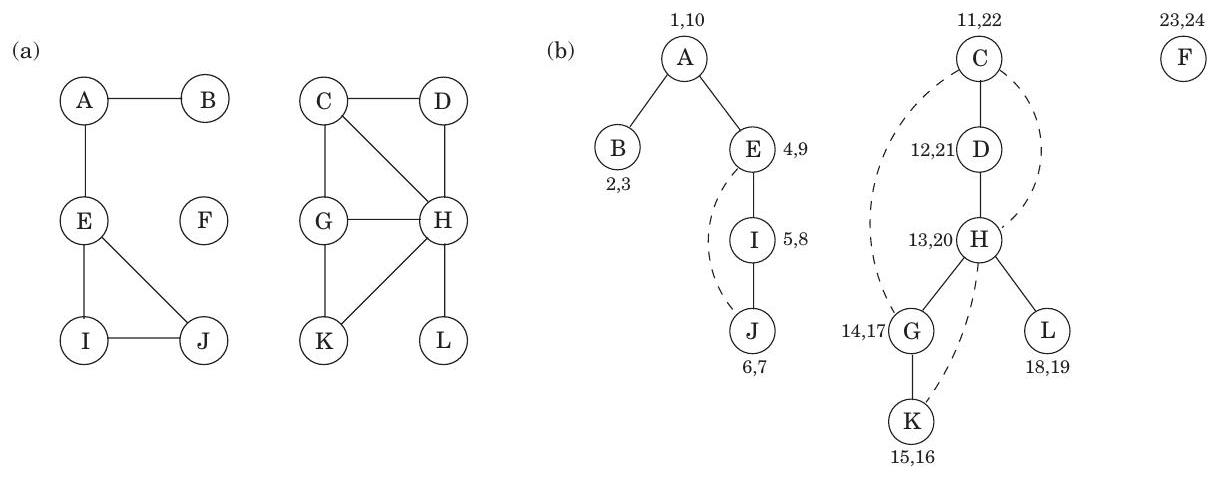
그림 3.6은 12개 노드 그래프에서 깊이 우선 탐색의 결과를 보여주며, 다시 한번 알파벳 순서로 동점을 처리한다(지금은 숫자 쌍을 무시한다). DFS의 외부 루프는 , 그리고 마지막으로 에 대해 explore를 세 번 호출한다. 그 결과, 이 시작점들 각각을 뿌리로 하는 세 개의 트리가 생성된다. 이들은 함께 **포레스트(forest)**를 구성한다.
3.2.3 Connectivity in undirected graphs
무방향 그래프는 모든 꼭짓점 쌍 사이에 경로가 있으면 **연결(connected)**되어 있다고 한다. 그림 3.6의 그래프는 예를 들어 에서 로 가는 경로가 없기 때문에 연결되어 있지 않다. 그러나 이 그래프는 다음과 같은 꼭짓점 집합에 해당하는 세 개의 서로소(disjoint)인 연결된 영역을 가지고 있다:
이러한 영역을 **연결 요소(connected components)**라고 한다. 각 연결 요소는 내부적으로는 연결되어 있지만 나머지 꼭짓점들과는 간선이 없는 서브그래프이다. explore가 특정 꼭짓점에서 시작되면, 해당 꼭짓점을 포함하는 연결 요소를 정확히 식별한다. 그리고 DFS 외부 루프가 explore를 호출할 때마다 새로운 연결 요소가 선택된다.
따라서 **깊이 우선 탐색(depth-first search)**은 그래프가 연결되어 있는지 확인하고, 더 일반적으로는 각 노드 에 해당 노드가 속한 연결 요소를 식별하는 정수 ccnum[v]를 할당하는 데 쉽게 적용될 수 있다. 필요한 것은 다음과 같다:
procedure previsit(v)
ccnum[v] = cc
여기서 cc는 0으로 초기화되어야 하며, DFS 프로시저가 explore를 호출할 때마다 1씩 증가해야 한다.
3.2.4 Previsit and postvisit orderings
우리는 몇 줄 안 되는 코드로 이루어진 **깊이 우선 탐색(depth-first search)**이 선형 시간 안에 무방향 그래프의 연결 구조를 어떻게 밝혀낼 수 있는지 살펴보았다. 그러나 깊이 우선 탐색은 이보다 훨씬 더 다재다능하다. 이를 더 확장하기 위해 탐색 과정에서 몇 가지 정보를 더 수집할 것이다. 각 노드에 대해 두 가지 중요한 이벤트 시간을 기록할 것이다: **첫 발견 시점(previsit에 해당)**과 **최종 이탈 시점(postvisit)**이다. 그림 3.6은 이전 예시에 대한 이 숫자들을 보여주며, 총 24개의 이벤트가 있다. 다섯 번째 이벤트는 의 발견이다. 21번째 이벤트는 를 완전히 떠나는 것으로 구성된다.
이 숫자들로 pre 및 post 배열을 생성하는 한 가지 방법은 처음에 1로 설정된 간단한 카운터 clock을 정의하고 다음과 같이 업데이트하는 것이다.
procedure previsit(v)
pre[v] = clock
clock = clock + 1
procedure postvisit(v)
post[v] = clock
clock = clock + 1
이러한 타이밍은 곧 더 큰 의미를 갖게 될 것이다. 한편, 그림 3.4에서 다음과 같은 사실을 알아차렸을 것이다.
속성: 임의의 노드 와 에 대해, 두 구간 와 는 서로 겹치지 않거나(disjoint) 하나가 다른 하나 안에 포함된다.
왜 그럴까? 는 본질적으로 정점 가 스택에 있었던 시간이기 때문이다. 스택의 후입선출(last-in, first-out) 특성이 나머지를 설명한다.
3.3 Depth-first search in directed graphs
3.3.1 Types of edges
우리의 깊이 우선 탐색(DFS) 알고리즘은 방향 그래프에서도 그대로 실행될 수 있으며, 이때 간선은 지정된 방향으로만 탐색하도록 주의해야 한다. 그림 3.7은 이러한 예시와 정점을 사전순으로 고려했을 때 생성되는 탐색 트리를 보여준다.
그림 3.7 방향 그래프에서의 DFS.
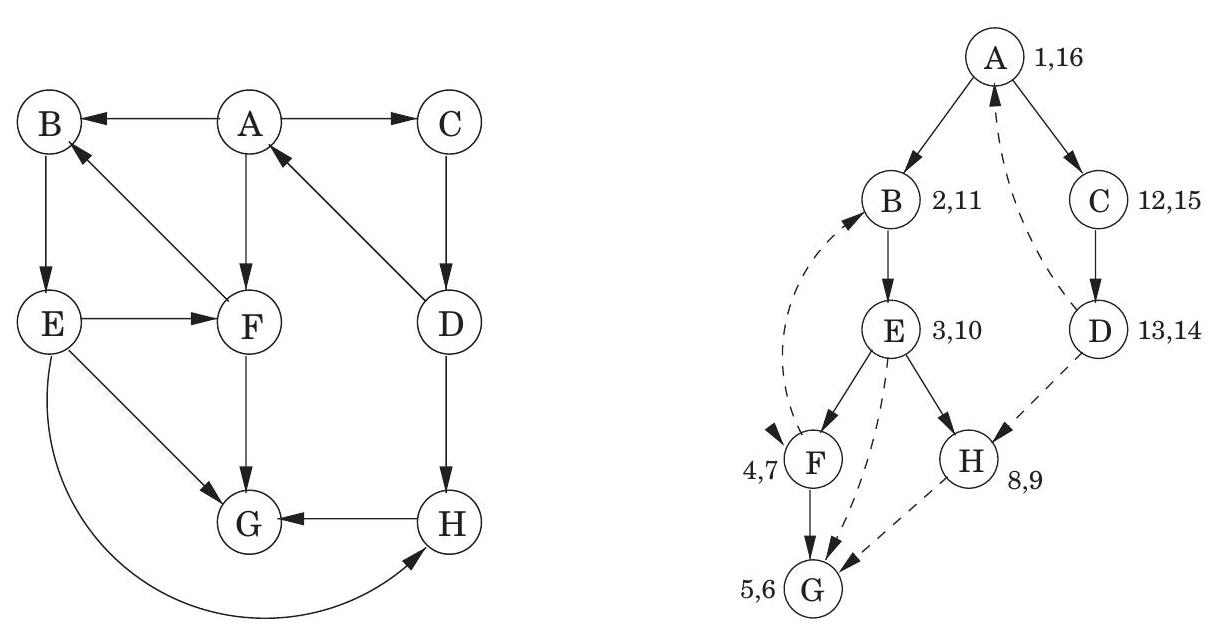
방향 그래프의 경우를 더 자세히 분석하기 위해, 트리의 노드들 간의 중요한 관계를 나타내는 용어를 사용하는 것이 도움이 된다. 는 탐색 트리의 **루트(root)**이며, 다른 모든 노드는 의 **자손(descendant)**이다. 마찬가지로, 는 를 자손으로 가지며, 반대로 는 이 세 노드의 **조상(ancestor)**이다. 이러한 가족 비유는 더 나아가 가 의 **부모(parent)**이고, 는 의 **자식(child)**이라는 식으로 이어진다.
무방향 그래프에서는 **트리 간선(tree edge)**과 **비트리 간선(nontree edge)**을 구분했다. 방향 그래프의 경우에는 약간 더 정교한 분류 체계가 있다:
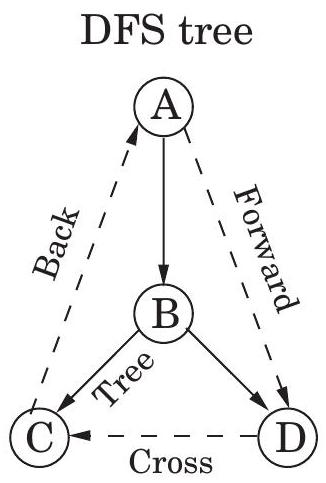
Tree edges는 실제로 DFS forest의 일부이다. Forward edges는 DFS 트리에서 노드에서 비자식 자손으로 이어진다.
Back edges는 DFS 트리에서 조상으로 이어진다. Cross edges는 자손도 조상도 아닌 노드로 이어진다. 따라서 이미 완전히 탐색된(즉, 이미 postvisited된) 노드로 이어진다.
그림 3.7에는 두 개의 forward edge, 두 개의 back edge, 그리고 두 개의 cross edge가 있다. 이들을 찾을 수 있는가?
조상 및 자손 관계와 간선 유형은 pre 및 post 번호에서 직접 읽어낼 수 있다. 깊이 우선 탐색(depth-first exploration) 전략 때문에, 정점 가 정점 의 조상인 경우는 가 먼저 발견되고 가 explore() 중에 발견되는 경우에 해당한다. 즉, **pre() < pre() < post() < post()**이며, 이를 두 개의 중첩된 구간으로 시각적으로 나타낼 수 있다:
자손의 경우는 대칭적이다. 가 의 자손인 것은 가 의 조상인 경우와 동일하기 때문이다. 그리고 간선 범주가 전적으로 조상-자손 관계에 기반하므로, 이들 또한 pre 및 post 번호에서 읽어낼 수 있다. 다음은 간선 ()에 대한 다양한 가능성을 요약한 것이다:
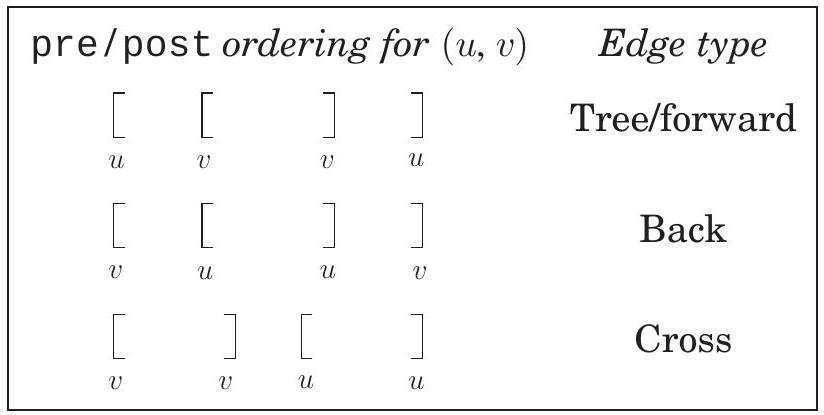
간선 유형 다이어그램을 참조하여 각 특성을 확인할 수 있다. 다른 순서가 불가능한 이유를 알겠는가?
3.3.2 Directed acyclic graphs
방향 그래프에서 cycle은 와 같은 순환 경로이다. 그림 3.7에는 와 같이 많은 cycle이 있다. cycle이 없는 그래프는 acyclic이다. 단일 depth-first search를 통해 선형 시간 안에 acyclicity를 테스트할 수 있다.
속성 방향 그래프는 depth-first search가 back edge를 발견하는 경우에만 cycle을 갖는다.
증명. 한 방향은 매우 쉽다: 만약 ()가 back edge라면, 이 edge와 search tree에서 에서 로 가는 경로로 구성된 cycle이 존재한다.
반대로, 그래프가 cycle을 갖는다면, 이 cycle에서 가장 먼저 발견된 노드(가장 낮은 pre number를 가진 노드)를 살펴보자. 그것이 라고 가정하자. cycle의 다른 모든 는 로부터 도달 가능하며, 따라서 search tree에서 의 descendant가 될 것이다. 특히, (또는 인 경우 ) edge는 노드에서 그 ancestor로 이어지므로 정의상 back edge이다. I
Directed acyclic graph, 줄여서 dag는 항상 나타난다. 이들은 인과 관계, 계층 구조, 시간적 종속성과 같은 관계를 모델링하는 데 유용하다. 예를 들어, 많은 task를 수행해야 하지만 일부 task는 특정 다른 task가 완료될 때까지 시작할 수 없다고 가정해 보자 (침대에서 일어나기 전에 잠에서 깨야 한다; 샤워를 하기 위해서는 침대에서 나와야 하지만 아직 옷을 입지 않은 상태여야 한다; 등). 그러면 질문은, task를 수행하는 유효한 순서는 무엇인가?
이러한 제약 조건은 각 task가 노드이고, 가 의 precondition인 경우 에서 로 가는 edge가 있는 방향 그래프로 편리하게 표현된다. 즉, task를 수행하기 전에, 그 task를 가리키는 모든 task가 완료되어야 한다. 이 그래프에 cycle이 있다면, 희망이 없다: 어떤 순서도 작동할 수 없다. 반면에 그래프가 dag라면, 우리는 가능하다면 그것을 linearize (또는 topologically sort)하여, 각 edge가 이전 vertex에서 이후 vertex로 가도록 vertex들을 차례로 정렬하여 모든 선행 제약 조건이 충족되도록 하고 싶다. 예를 들어, 그림 3.8에서 유효한 순서 중 하나는 이다. (다른 세 가지를 찾을 수 있는가?)
그림 3.8 하나의 source, 두 개의 sink, 그리고 네 가지 가능한 linearization을 가진 directed acyclic graph.
어떤 유형의 dag가 linearize될 수 있는가? 간단하다: 모든 dag가 가능하다. 그리고 다시 한번 depth-first search가 그것을 수행하는 방법을 정확히 알려준다: 단순히 post number의 내림차순으로 task를 수행하면 된다. 결국, 그래프에서 post() < post()인 유일한 edge ()는 back edge이다 (88페이지의 edge 유형 표를 상기하라) - 그리고 우리는 dag가 back edge를 가질 수 없다는 것을 보았다. 그러므로:
속성 dag에서 모든 edge는 더 낮은 post number를 가진 vertex로 이어진다. 이것은 dag의 노드를 정렬하는 선형 시간 알고리즘을 제공한다. 그리고 우리의 이전 관찰과 함께, 이것은 세 가지 상당히 다르게 들리는 속성들 - acyclicity, linearizability, 그리고 depth-first search 중 back edge의 부재 -이 사실상 동일한 것임을 알려준다.
dag는 post number의 내림차순으로 linearize되므로, 가장 작은 post number를 가진 vertex가 이 linearization에서 마지막에 오며, 그것은 sink여야 한다 - 나가는 edge가 없는 노드. 대칭적으로, 가장 높은 post number를 가진 노드는 source이며, 들어오는 edge가 없는 노드이다.
속성 모든 dag는 적어도 하나의 source와 적어도 하나의 sink를 갖는다. source의 보장된 존재는 linearization에 대한 대안적인 접근 방식을 제시한다:
source를 찾고, 출력하고, 그래프에서 삭제한다. 그래프가 비어 있을 때까지 반복한다. 이것이 모든 dag에 대해 유효한 linearization을 생성하는 이유를 알 수 있는가? 그래프에 cycle이 있다면 어떻게 되는가? 그리고 이 알고리즘은 어떻게 선형 시간 안에 구현될 수 있는가? (연습 문제 3.14.)
3.4 Strongly connected components
3.4.1 Defining connectivity for directed graphs
무방향 그래프에서의 **연결성(connectivity)**은 매우 간단하다. 연결되지 않은 그래프는 자연스럽고 명확한 방식으로 여러 개의 **연결된 컴포넌트(connected components)**로 분해될 수 있다(그림 3.6이 좋은 예시이다). 섹션 3.2.3에서 보았듯이, **깊이 우선 탐색(depth-first search)**은 각 재시작이 새로운 연결된 컴포넌트를 표시하면서 이 작업을 손쉽게 수행한다.
방향 그래프에서 연결성은 더 미묘하다. 어떤 원시적인 의미에서 그림 3.9(a)의 방향 그래프는 "연결되어 있다"—간선을 끊지 않고서는 "분리될 수 없다"고 말할 수 있다. 그러나 이러한 개념은 흥미롭거나 유익하지 않다. 예를 들어 에서 로 가는 경로가 없거나 에서 로 가는 경로가 없기 때문에 이 그래프는 연결되어 있다고 볼 수 없다. 방향 그래프의 연결성을 정의하는 올바른 방법은 다음과 같다:
방향 그래프의 두 노드 와 는 에서 로 가는 경로와 에서 로 가는 경로가 모두 있을 때 연결되어 있다.
그림 3.9 (a) 방향 그래프와 그 강하게 연결된 컴포넌트(strongly connected components). (b) 메타 그래프(meta-graph).
(a)
(b)
이 관계는 를 강하게 연결된 컴포넌트라고 부르는 서로소 집합으로 분할한다(연습문제 3.30). 그림 3.9(a)의 그래프에는 다섯 개의 강하게 연결된 컴포넌트가 있다.
이제 각 강하게 연결된 컴포넌트를 단일 **메타 노드(meta-node)**로 축소하고, 해당 컴포넌트들 사이에 간선(동일한 방향)이 있으면 한 메타 노드에서 다른 메타 노드로 간선을 그린다(그림 3.9(b)). 결과로 생성되는 메타 그래프는 **DAG(Directed Acyclic Graph)**여야 한다. 그 이유는 간단하다: 여러 강하게 연결된 컴포넌트를 포함하는 사이클은 이들을 모두 단일의 강하게 연결된 컴포넌트로 병합할 것이기 때문이다. 다시 말해,
속성: 모든 방향 그래프는 그 강하게 연결된 컴포넌트들의 DAG이다. 이는 우리에게 중요한 것을 알려준다: 방향 그래프의 연결성 구조는 두 계층으로 이루어져 있다. 최상위 계층에는 DAG가 있는데, 이는 선형화될 수 있는 등 비교적 간단한 구조이다. 더 세부적인 정보가 필요하다면, 이 DAG의 노드 중 하나를 들여다보고 그 안에 있는 완전한 강하게 연결된 컴포넌트를 조사할 수 있다.
3.4.2 An efficient algorithm
방향 그래프를 **강하게 연결된 구성 요소(strongly connected components)**로 분해하는 것은 매우 유익하고 유용하다. 다행히도, **깊이 우선 탐색(depth-first search)**을 추가로 활용하여 선형 시간 안에 이를 찾을 수 있다. 이 알고리즘은 우리가 이미 보았지만 이제 더 자세히 살펴볼 몇 가지 속성을 기반으로 한다.
속성 1 explore 서브루틴이 노드 에서 시작되면, 에서 도달 가능한 모든 노드가 방문되었을 때 정확히 종료된다.
따라서, 싱크 강하게 연결된 구성 요소(sink strongly connected component)(메타그래프에서 싱크인 강하게 연결된 구성 요소)에 있는 노드에서 explore를 호출하면, 정확히 해당 구성 요소를 검색하게 된다. 그림 3.9에는 두 개의 싱크 강하게 연결된 구성 요소가 있다. 예를 들어, 노드 에서 explore를 시작하면 더 큰 구성 요소를 완전히 탐색한 다음 멈출 것이다.
이는 하나의 강하게 연결된 구성 요소를 찾는 방법을 제시하지만, 여전히 두 가지 주요 문제를 남긴다: (A) 싱크 강하게 연결된 구성 요소에 확실히 속하는 노드를 어떻게 찾을 수 있는가? (B) 이 첫 번째 구성 요소를 발견한 후 어떻게 계속 진행하는가?
문제 (A)부터 시작해보자. 싱크 강하게 연결된 구성 요소에 속한다고 보장되는 노드를 쉽게 직접적으로 선택하는 방법은 없다. 하지만 **소스 강하게 연결된 구성 요소(source strongly connected component)**에 있는 노드를 얻는 방법은 있다.
속성 2 깊이 우선 탐색에서 가장 높은 post number를 받는 노드는 소스 강하게 연결된 구성 요소에 속해야 한다.
이는 다음의 더 일반적인 속성에서 비롯된다.
그림 3.10 그림 3.9의 그래프를 뒤집은 것.
속성 3 와 가 강하게 연결된 구성 요소이고, 의 노드에서 의 노드로 가는 엣지가 있다면, 의 가장 높은 post number는 의 가장 높은 post number보다 크다.
증명. 속성 3을 증명할 때, 두 가지 경우를 고려해야 한다. 깊이 우선 탐색이 구성 요소 를 보다 먼저 방문하는 경우, 분명히 와 전체가 프로시저가 멈추기 전에 탐색될 것이다(속성 1 참조). 따라서 에서 처음 방문된 노드는 의 어떤 노드보다 더 높은 post number를 가질 것이다. 반면에, 가 먼저 방문되는 경우, 깊이 우선 탐색은 전체를 본 후에 를 보기 전에 멈출 것이며, 이 경우 속성은 즉시 성립한다.
속성 3은 강하게 연결된 구성 요소들을 가장 높은 post number의 내림차순으로 배열함으로써 선형화할 수 있다고 재진술될 수 있다. 이는 dag를 선형화하는 우리의 이전 알고리즘의 일반화이다. dag에서는 각 노드가 단일 강하게 연결된 구성 요소이다.
속성 2는 의 소스 강하게 연결된 구성 요소에 있는 노드를 찾는 데 도움이 된다. 그러나 우리가 필요한 것은 싱크 구성 요소에 있는 노드이다. 우리의 수단은 우리의 필요와 반대되는 것처럼 보인다! 하지만 역방향 그래프(reverse graph) 을 고려해보자. 은 와 동일하지만 모든 엣지가 뒤집혀 있다(그림 3.10). 은 와 정확히 동일한 강하게 연결된 구성 요소를 갖는다(왜 그럴까?). 따라서 에 대해 깊이 우선 탐색을 수행하면, 가장 높은 post number를 가진 노드는 의 소스 강하게 연결된 구성 요소에서 나올 것이며, 이는 의 싱크 강하게 연결된 구성 요소에 해당한다. 우리는 문제 (A)를 해결했다!
문제 (B)로 넘어가자. 첫 번째 싱크 구성 요소가 식별된 후 어떻게 계속 진행하는가? 해결책은 속성 3에 의해 제공된다. 첫 번째 강하게 연결된 구성 요소를 찾아서 그래프에서 삭제하면, 노드는
Crawling fast
이 모든 것은 그래프가 정점 번호가 1부터 까지 매겨져 있고 간선이 인접 리스트에 깔끔하게 정리되어 우리에게 주어졌다고 가정한다. 그러나 월드 와이드 웹(World Wide Web)의 현실은 매우 다르다. 웹 그래프의 노드는 미리 알려져 있지 않으며, 검색 과정에서 하나씩 발견되어야 한다. 그리고 물론, 재귀(recursion)는 불가능하다.
그럼에도 불구하고, 웹 크롤링은 **깊이 우선 탐색(depth-first search)**과 매우 유사한 알고리즘으로 수행된다. 명시적인 스택이 유지되며, 이 스택에는 (하이퍼링크의 끝점으로) 발견되었지만 아직 탐색되지 않은 모든 노드가 포함된다. 사실, 이 "스택"은 정확히 후입선출(last-in, first-out) 리스트가 아니다. 가장 최근에 삽입된 노드(또는 가장 먼저 삽입된 노드, 이는 너비 우선 탐색(breadth-first search)이 될 것이다. 2장 참조)에 가장 높은 우선순위를 부여하는 것이 아니라, 가장 "흥미로워 보이는" 노드에 우선순위를 부여한다. 이는 스택이 넘치는 것을 방지하고, 최악의 경우, 광대한 새로운 영역으로 이어질 가능성이 매우 낮은 노드만 탐색되지 않은 상태로 남겨두기 위한 휴리스틱(heuristic) 기준이다.
실제로 크롤링은 일반적으로 여러 컴퓨터가 동시에 탐색을 실행하여 수행된다. 각 컴퓨터는 스택의 맨 위에서 탐색할 다음 노드를 가져와서 http 파일(서로를 가리키는 웹 파일의 종류)을 다운로드하고, 하이퍼링크를 찾기 위해 스캔한다. 그러나 하이퍼링크 끝에서 새로운 http 문서가 발견되면 재귀 호출은 이루어지지 않는다. 대신, 새로운 정점은 중앙 스택에 삽입된다.
하지만 한 가지 질문이 남는다. "새로운" 문서를 볼 때, 그것이 정말 새로운 문서인지, 즉 크롤링 과정에서 이전에 본 적이 없는 문서인지 어떻게 알 수 있을까? 그리고 스택에 삽입하고 "이미 본" 것으로 기록할 수 있도록 어떻게 이름을 부여할까? 그 답은 해싱(hashing)에 있다.
덧붙여, 연구자들은 웹에서 강하게 연결된 구성 요소(strongly connected components) 알고리즘을 실행하여 매우 흥미로운 구조를 발견했다. 남아 있는 것들 중에서 가장 높은 post number는 의 남은 부분 중 싱크(sink) 강하게 연결된 구성 요소에 속할 것이다. 따라서 우리는 에 대한 초기 깊이 우선 탐색에서 얻은 post numbering을 계속 사용하여 두 번째 강하게 연결된 구성 요소, 세 번째 강하게 연결된 구성 요소 등을 연속적으로 출력할 수 있다. 결과 알고리즘은 다음과 같다.
- 에 대해 깊이 우선 탐색을 실행한다.
- 에 대해 무방향 연결 구성 요소(undirected connected components) 알고리즘(3.2.3절 참조)을 실행하고, 깊이 우선 탐색 중에 1단계에서 얻은 post number의 내림차순으로 정점들을 처리한다.
이 알고리즘은 **선형 시간(linear-time)**이며, 선형 항의 상수는 일반적인 깊이 우선 탐색의 약 두 배이다. (질문: 선형 시간으로 의 인접 리스트 표현을 어떻게 구성하는가? 그리고 선형 시간으로 의 정점들을 post 값의 내림차순으로 어떻게 정렬하는가?)
그림 3.9의 그래프에 이 알고리즘을 실행해 보자. 1단계가 정점들을 사전 순서로 고려한다면, 2단계(즉, 의 깊이 우선 탐색에서 post number의 내림차순)를 위해 설정하는 순서는 다음과 같다: . 그러면 2단계는 다음 순서로 구성 요소들을 분리한다: .
Exercises
3.1. 다음 그래프에 대해 **깊이 우선 탐색(DFS)**을 수행하고, 정점을 선택할 때마다 알파벳 순서로 가장 먼저 오는 것을 선택하라. 각 edge를 tree edge 또는 back edge로 분류하고, 각 정점의 pre 및 post number를 부여하라.
 3.2. 다음 각 그래프에 대해 **깊이 우선 탐색(DFS)**을 수행하고, 정점을 선택할 때마다 알파벳 순서로 가장 먼저 오는 것을 선택하라. 각 edge를 tree edge, forward edge, back edge 또는 cross edge로 분류하고, 각 정점의 pre 및 post number를 부여하라.
3.2. 다음 각 그래프에 대해 **깊이 우선 탐색(DFS)**을 수행하고, 정점을 선택할 때마다 알파벳 순서로 가장 먼저 오는 것을 선택하라. 각 edge를 tree edge, forward edge, back edge 또는 cross edge로 분류하고, 각 정점의 pre 및 post number를 부여하라.
(a)
(b)

3.3. 다음 그래프에 대해 DFS 기반 위상 정렬(topological ordering) 알고리즘을 실행하라. 탐색할 정점을 선택할 때마다 항상 알파벳 순서로 가장 먼저 오는 것을 선택하라.
 (a) 노드의 pre 및 post number를 표시하라.
(b) 그래프의 source와 sink는 무엇인가?
(c) 알고리즘에 의해 찾아지는 위상 정렬은 무엇인가?
(d) 이 그래프는 몇 개의 위상 정렬을 가지는가?
3.4. 다음 방향 그래프 에 대해 강하게 연결된 구성 요소(strongly connected components, SCCs) 알고리즘을 실행하라. 에 대해 DFS를 수행할 때, 탐색할 정점을 선택할 때마다 항상 알파벳 순서로 가장 먼저 오는 것을 선택하라.
(a) 노드의 pre 및 post number를 표시하라.
(b) 그래프의 source와 sink는 무엇인가?
(c) 알고리즘에 의해 찾아지는 위상 정렬은 무엇인가?
(d) 이 그래프는 몇 개의 위상 정렬을 가지는가?
3.4. 다음 방향 그래프 에 대해 강하게 연결된 구성 요소(strongly connected components, SCCs) 알고리즘을 실행하라. 에 대해 DFS를 수행할 때, 탐색할 정점을 선택할 때마다 항상 알파벳 순서로 가장 먼저 오는 것을 선택하라.
 (ii)
(ii)
각 경우에 다음 질문에 답하라. (a) **강하게 연결된 구성 요소(SCCs)**는 어떤 순서로 찾아지는가? (b) 어떤 SCC가 source SCC이고 어떤 SCC가 sink SCC인가? (c) "메타그래프(metagraph)"를 그려라 (각 메타 노드는 의 SCC이다). (d) 이 그래프를 강하게 연결된(strongly connected) 상태로 만들기 위해 추가해야 하는 최소 edge 수는 얼마인가? 3.5. 방향 그래프 의 역방향(reverse) 는 동일한 정점 집합을 가지지만 모든 edge가 역방향인 또 다른 방향 그래프이다. 즉, 이다.
인접 리스트(adjacency list) 형식으로 주어진 그래프의 역방향을 계산하는 선형 시간 알고리즘을 제시하라. 3.6. 무방향 그래프에서 정점 의 차수(degree) 는 가 가진 이웃의 수, 또는 동등하게 에 인접한 edge의 수이다. 방향 그래프에서는 로 들어오는 edge의 수인 진입 차수(indegree) 와 에서 나가는 edge의 수인 진출 차수(outdegree) 를 구별한다. (a) 무방향 그래프에서 임을 보여라. (b) (a) 부분을 사용하여 무방향 그래프에서 차수가 홀수인 정점의 수가 짝수여야 함을 보여라. (c) 방향 그래프에서 진입 차수가 홀수인 정점의 수에 대해 유사한 진술이 성립하는가? 3.7. **이분 그래프(bipartite graph)**는 정점들이 두 집합( 및 )으로 분할될 수 있고, 동일한 집합 내의 정점들 사이에는 edge가 없는 그래프 이다 (예를 들어, 이면 와 사이에는 edge가 없다). (a) 무방향 그래프가 이분 그래프인지 여부를 결정하는 선형 시간 알고리즘을 제시하라. (b) 이 속성을 공식화하는 다른 많은 방법들이 있다. 예를 들어, 무방향 그래프는 두 가지 색으로만 색칠할 수 있는 경우에만 이분 그래프이다.
다음 공식을 증명하라: 무방향 그래프는 홀수 길이의 cycle을 포함하지 않는 경우에만 이분 그래프이다. (c) 정확히 하나의 홀수 길이 cycle을 가진 무방향 그래프를 색칠하는 데 최대 몇 개의 색이 필요한가? 3.8. 물 붓기. 각각 10파인트, 7파인트, 4파인트 크기의 세 개의 용기가 있다. 7파인트와 4파인트 용기는 물로 가득 차 있지만, 10파인트 용기는 처음에는 비어 있다. 우리는 한 가지 유형의 작업만 허용한다: 한 용기의 내용물을 다른 용기에 붓는 것으로, 원본 용기가 비거나 대상 용기가 가득 찰 때만 멈춘다. 우리는 7파인트 또는 4파인트 용기에 정확히 2파인트가 남는 붓기 순서가 있는지 알고 싶다. (a) 이를 그래프 문제로 모델링하라: 관련된 그래프에 대한 정확한 정의를 제시하고, 이 그래프에 대해 답해야 할 특정 질문을 명시하라. (b) 이 문제를 해결하기 위해 어떤 알고리즘을 적용해야 하는가? 3.9. 무방향 그래프의 각 노드 에 대해, **twodegree **를 의 이웃들의 차수 합으로 정의한다. 인접 리스트 형식으로 주어진 그래프에서 전체 twodegree[.] 값 배열을 선형 시간에 계산하는 방법을 보여라. 3.10. explore 프로시저(그림 3.3)를 **비재귀적(non-recursive)**으로 다시 작성하라 (즉, 명시적으로 스택을 사용하라). previsit 및 postvisit 호출은 재귀 프로시저와 동일한 효과를 가지도록 배치되어야 한다. 3.11. 무방향 그래프 와 그 안에 있는 특정 edge 가 주어졌을 때, 가 를 포함하는 cycle을 가지는지 여부를 결정하는 선형 시간 알고리즘을 설계하라. 3.12. 증명하거나 반례를 제시하라: 무방향 그래프에서 가 edge이고, 깊이 우선 탐색 중에 post post 이면, 는 DFS tree에서 의 조상이다. 3.13. 무방향 vs. 방향 연결성. (a) 모든 연결된 무방향 그래프 에서, 제거하면 가 여전히 연결된 상태로 남아 있는 정점 가 존재함을 증명하라. (힌트: 에 대한 DFS 탐색 트리를 고려하라.) (b) 모든 에 대해, 를 에서 제거하면 강하게 연결되지 않은 방향 그래프가 되는 강하게 연결된 방향 그래프 의 예를 제시하라. (c) 2개의 연결된 구성 요소를 가진 무방향 그래프에서는 항상 하나의 edge만 추가하여 그래프를 연결된 상태로 만들 수 있다. 두 개의 강하게 연결된 구성 요소를 가진 방향 그래프의 예를 제시하고, 하나의 edge를 추가해도 그래프를 강하게 연결된 상태로 만들 수 없음을 보여라. 3.14. 이 장에서는 선형화(위상 정렬)를 위한 대체 알고리즘을 제안한다. 이 알고리즘은 그래프에서 source node를 반복적으로 제거한다(90페이지). 이 알고리즘이 선형 시간에 구현될 수 있음을 보여라. 3.15. Computopia 시의 경찰서는 모든 도로를 일방통행으로 만들었다. 시장은 여전히 도시의 어떤 교차로에서든 다른 어떤 교차로로 합법적으로 운전할 수 있는 방법이 있다고 주장하지만, 야당은 확신하지 못한다. 시장의 주장이 옳은지 판단하기 위한 컴퓨터 프로그램이 필요하다. 그러나 시 선거가 곧 다가오고 있으며, 선형 시간 알고리즘을 실행할 시간만 있다. (a) 이 문제를 그래프 이론적으로 공식화하고, 왜 선형 시간에 해결될 수 있는지 설명하라. (b) 이제 시장의 원래 주장이 거짓으로 밝혀졌다고 가정하자. 그녀는 다음으로 더 약한 주장을 한다: 시청에서 운전을 시작하여 일방통행 도로를 따라가면, 어디에 도달하든 항상 합법적으로 시청으로 돌아올 수 있는 방법이 있다. 이 더 약한 속성을 그래프 이론 문제로 공식화하고, 이것 역시 선형 시간에 확인할 수 있는 방법을 신중하게 보여라. 3.16. CS 커리큘럼이 개의 필수 과목으로 구성되어 있다고 가정하자. 선수 과목 그래프(prerequisite graph) 는 각 과목에 대한 노드를 가지며, 가 의 선수 과목인 경우에만 과목 에서 과목 로의 edge를 가진다. 이 그래프 표현을 직접 사용하여 커리큘럼을 완료하는 데 필요한 최소 학기 수를 계산하는 알고리즘을 찾아라 (학생은 한 학기에 몇 개의 과목이든 수강할 수 있다고 가정한다). 알고리즘의 실행 시간은 선형이어야 한다. 3.17. 무한 경로. 가 지정된 "시작 정점" , "좋은" 정점 집합 , "나쁜" 정점 집합 를 가진 방향 그래프라고 하자. 의 무한 trace 는 정점 의 무한 시퀀스 로, (1) 이고, (2) 모든 에 대해 를 만족한다. 즉, 는 정점 에서 시작하는 의 무한 경로이다. 정점 집합 가 유한하므로, 의 모든 무한 trace는 일부 정점을 무한히 자주 방문해야 한다. (a) 가 무한 trace인 경우, 를 에서 무한히 자주 나타나는 정점들의 집합이라고 하자. 가 의 **강하게 연결된 구성 요소(strongly connected component)**의 부분 집합임을 보여라. (b) 가 무한 trace를 가지는지 여부를 결정하는 알고리즘을 설명하라. (c) 가 의 일부 좋은 정점을 무한히 자주 방문하는 무한 trace를 가지는지 여부를 결정하는 알고리즘을 설명하라. (d) 가 의 일부 좋은 정점을 무한히 자주 방문하지만, 의 나쁜 정점은 무한히 자주 방문하지 않는 무한 trace를 가지는지 여부를 결정하는 알고리즘을 설명하라. 3.18. 지정된 root node 와 함께 이진 트리 (인접 리스트 형식)가 주어진다. rooted tree에서 는 에서 로 가는 경로가 를 통과하는 경우 의 조상이라고 한다.
" 가 의 조상인가?"와 같은 쿼리에 상수 시간에 답할 수 있도록 트리를 전처리하려고 한다. 전처리 자체는 선형 시간이 걸려야 한다. 어떻게 할 수 있는가? 3.19. 이전 문제와 마찬가지로, 지정된 root node를 가진 이진 트리 가 주어진다. 또한, 의 각 노드에 대한 값을 가진 배열 가 있다. 새로운 배열 를 다음과 같이 정의한다: 각 에 대해, 의 자손들과 관련된 -값들의 최댓값. 전체 -배열을 계산하는 선형 시간 알고리즘을 제시하라. 3.20. 지정된 root node 와 함께 트리 가 주어진다. 인 모든 노드 의 부모 는 에서 로 가는 경로에서 에 인접한 노드로 정의된다. 관례적으로 이다. 에 대해 및 로 정의한다 (따라서 는 의 번째 조상이다).
트리의 각 정점 는 연관된 음이 아닌 정수 레이블 를 가진다. 다음 규칙에 따라 의 모든 정점의 레이블을 업데이트하는 선형 시간 알고리즘을 제시하라: . 3.21. 방향 그래프에서 홀수 길이 cycle을 찾는 선형 시간 알고리즘을 제시하라. (힌트: 먼저 그래프가 강하게 연결되어 있다고 가정하고 이 문제를 해결하라.) 3.22. 방향 그래프 를 입력으로 받아, 모든 다른 정점에 도달할 수 있는 정점 가 있는지 여부를 결정하는 효율적인 알고리즘을 제시하라. 3.23. 방향 비순환 그래프 와 두 정점 를 입력으로 받아, 에서 에서 까지의 서로 다른 방향 경로의 수를 출력하는 효율적인 알고리즘을 제시하라. 3.24. 다음 작업을 위한 선형 시간 알고리즘을 제시하라.
입력: 방향 비순환 그래프
질문: 는 모든 정점을 정확히 한 번씩 방문하는 방향 경로를 포함하는가?
3.25. 각 노드 에 양의 정수인 연관된 가격 가 있는 방향 그래프가 주어진다. 배열 cost를 다음과 같이 정의한다: 각 에 대해,
cost 에서 도달할 수 있는 가장 저렴한 노드의 가격 ( 자신 포함).
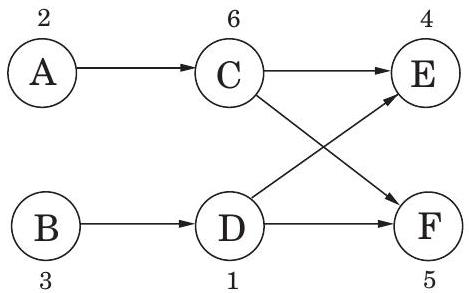
예를 들어, 아래 그래프(각 정점에 가격이 표시됨)에서 노드 의 cost 값은 각각 이다.
목표는 전체 cost 배열을 채우는 알고리즘을 설계하는 것이다 (즉, 모든 정점에 대해). (a) 방향 비순환 그래프에 대해 작동하는 선형 시간 알고리즘을 제시하라. (힌트: 특정 순서로 정점을 처리하라.) (b) 이를 모든 방향 그래프에 대해 작동하는 선형 시간 알고리즘으로 확장하라. (힌트: 방향 그래프의 "두 계층" 구조를 상기하라.) 3.26. 무방향 그래프의 **오일러 투어(Eulerian tour)**는 각 정점을 여러 번 통과할 수 있지만, 각 edge를 정확히 한 번만 사용해야 하는 cycle이다.
이 간단한 개념은 오일러가 1736년에 유명한 쾨니히스베르크 다리 문제를 해결하는 데 사용되었으며, 이는 그래프 이론 분야를 시작하게 했다. 쾨니히스베르크(현재는 러시아 서부의 칼리닌그라드)는 두 강이 만나고 중간에 작은 섬이 있는 지점이다. 강을 가로지르는 7개의 다리가 있었고, 당시 인기 있는 여가 질문은 각 다리를 정확히 한 번씩 건너는 투어를 수행하는 것이 가능한지 여부를 결정하는 것이었다.
오일러는 관련 정보를 4개의 노드(육지를 나타냄)와 7개의 edge(다리를 나타냄)를 가진 그래프로 공식화했다.
 남쪽 강둑
남쪽 강둑
이 문제의 특이한 점에 주목하라: 특정 노드 쌍 사이에 여러 edge가 존재한다. (a) 무방향 그래프가 오일러 투어를 가지는 경우에만 모든 정점이 짝수 차수를 가짐을 보여라. 쾨니히스베르크 다리에는 오일러 투어가 없음을 결론지어라. (b) **오일러 경로(Eulerian path)**는 각 edge를 정확히 한 번만 사용하는 경로이다. 어떤 무방향 그래프가 오일러 경로를 가지는지에 대한 유사한 필요충분조건 특성화를 제시할 수 있는가? (c) 방향 그래프에 대해 (a) 부분의 유사한 것을 제시할 수 있는가? 3.27. 그래프에서 두 경로는 공통 edge가 없는 경우 edge-disjoint라고 불린다. 모든 무방향 그래프에서 홀수 차수를 가진 정점들을 짝지어 각 쌍 사이에 경로를 찾을 수 있으며, 이 모든 경로가 edge-disjoint임을 보여라. 3.28. 2SAT 문제에서, 각 절이 두 리터럴(리터럴은 부울 변수 또는 부울 변수의 부정)의 논리합(OR)인 절 집합이 주어진다. 모든 절이 만족되도록 각 변수에 참 또는 거짓 값을 할당하는 방법을 찾고 있다. 즉, 각 절에 적어도 하나의 참 리터럴이 있어야 한다. 예를 들어, 다음은 2SAT의 인스턴스이다:
이 인스턴스는 만족하는 할당을 가진다: 를 각각 참, 거짓, 거짓, 참으로 설정한다. (a) 이 2SAT 공식에 대해 만족하는 다른 진리 할당이 있는가? 있다면, 모두 찾아라. (b) 네 개의 변수를 가지고 만족하는 할당이 없는 2SAT 인스턴스를 제시하라.
이 문제의 목적은 2SAT를 방향 그래프의 **강하게 연결된 구성 요소(strongly connected components)**를 찾는 문제로 환원하여 효율적으로 해결하는 방법을 제시하는 것이다. 개의 변수와 개의 절을 가진 2SAT 인스턴스 가 주어졌을 때, 다음과 같이 방향 그래프 를 구성한다.
- 는 각 변수와 그 부정에 대해 하나씩, 총 개의 노드를 가진다.
- 는 개의 edge를 가진다: 의 각 절 (여기서 는 리터럴)에 대해, 는 의 부정에서 로 가는 edge와 의 부정에서 로 가는 edge를 가진다. 절 는 함의 또는 중 하나와 동등하다는 점에 유의하라. 이러한 의미에서 는 의 모든 함의를 기록한다. (c) 위에 주어진 2SAT 인스턴스와 (b)에서 구성한 인스턴스에 대해 이 구성을 수행하라. (d) 가 어떤 변수 에 대해 와 를 모두 포함하는 강하게 연결된 구성 요소를 가지면, 는 만족하는 할당을 가지지 않음을 보여라. (e) 이제 (d)의 역을 보여라: 즉, 의 어떤 강하게 연결된 구성 요소도 리터럴과 그 부정을 모두 포함하지 않으면, 인스턴스 는 만족 가능해야 한다. (힌트: 변수에 값을 다음과 같이 할당하라: 의 sink 강하게 연결된 구성 요소를 반복적으로 선택한다. sink에 있는 모든 리터럴에 참 값을 할당하고, 그 부정에는 거짓 값을 할당한 다음, 이들 모두를 삭제한다. 이것이 만족하는 할당을 발견하게 됨을 보여라.) (f) 2SAT를 해결하기 위한 선형 시간 알고리즘이 있음을 결론지어라. 3.29. 를 유한 집합이라고 하자. 에 대한 **이항 관계(binary relation)**는 단순히 의 순서쌍 의 모음 이다. 예를 들어, 는 사람들의 집합일 수 있고, 각 쌍 은 "는 를 안다"를 의미할 수 있다.
**동치 관계(equivalence relation)**는 세 가지 속성을 만족하는 이항 관계이다:
- 반사성(Reflexivity): 모든 에 대해
- 대칭성(Symmetry): 이면
- 추이성(Transitivity): 이고 이면
예를 들어, "생일이 같은" 이항 관계는 동치 관계이지만, "의 아버지인"은 세 가지 속성을 모두 위반하므로 동치 관계가 아니다.
동치 관계가 집합 를 서로소 그룹 로 분할함을 보여라 (즉, 이고 모든 에 대해 ) 다음을 만족하도록:
- 그룹의 모든 두 구성원은 관련되어 있다. 즉, 모든 에 대해, 모든 에 대해 이다.
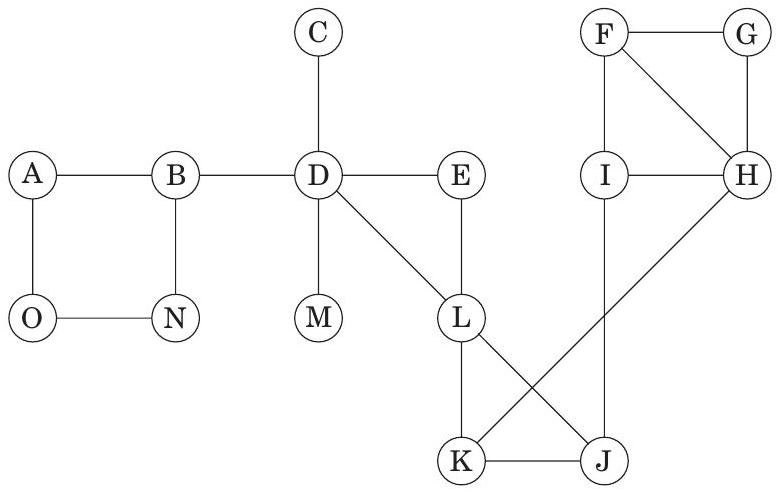
- 다른 그룹의 구성원은 관련되어 있지 않다. 즉, 모든 에 대해, 모든 및 에 대해 이다. (힌트: 동치 관계를 무방향 그래프로 나타내라.) 3.30. 91페이지에서 우리는 방향 그래프의 정점 집합에 대한 이항 관계 "연결됨(connected)"을 정의했다. 이것이 동치 관계(연습 문제 3.29 참조)임을 보여주고, 이것이 정점들을 서로소 **강하게 연결된 구성 요소(strongly connected components)**로 분할함을 결론지어라. 3.31. 이중 연결 구성 요소(Biconnected components). 를 무방향 그래프라고 하자. 임의의 두 edge 에 대해, 는 이거나 와 를 모두 포함하는 (단순) cycle이 있는 경우라고 말한다. (a) 가 edge에 대한 동치 관계(연습 문제 3.29 참조)임을 보여라.
이 관계가 edge를 분할하는 동치 클래스를 의 이중 연결 구성 요소라고 한다. Bridge는 그 자체로 이중 연결 구성 요소에 있는 edge이다.
**분리 정점(separating vertex)**은 제거하면 그래프를 단절시키는 정점이다.
(b) 아래 그래프의 edge를 이중 연결 구성 요소로 분할하고, bridge와 분리 정점을 식별하라.
이중 연결 구성 요소는 그래프의 edge를 분할할 뿐만 아니라, 다음 의미에서 정점도 거의 분할한다. (c) 각 이중 연결 구성 요소에 해당 edge의 끝점인 모든 정점을 연결하라. 두 개의 다른 이중 연결 구성 요소에 해당하는 정점들이 서로소이거나 단일 분리 정점에서 교차함을 보여라. (d) 각 이중 연결 구성 요소를 단일 메타 노드로 축소하고, 각 분리 정점에 대해 개별 노드를 유지하라. (따라서 각 구성 요소 노드와 그 분리 정점 사이에 edge가 있다.) 결과 그래프가 트리임을 보여라.
DFS는 그래프의 이중 연결 구성 요소, bridge 및 분리 정점을 선형 시간에 식별하는 데 사용될 수 있다. (e) DFS 트리의 root는 트리에 두 개 이상의 자식을 가지는 경우에만 분리 정점임을 보여라. (f) DFS 트리의 non-root 정점 는 자식 를 가지며, 의 어떤 자손(자신 포함)도 의 적절한 조상으로 가는 backedge를 가지지 않는 경우에만 분리 정점임을 보여라. (g) 각 정점 에 대해 다음을 정의하라:
전체 low 값 배열이 선형 시간에 계산될 수 있음을 보여라. (h) 그래프의 모든 분리 정점, bridge, 이중 연결 구성 요소를 선형 시간에 계산하는 방법을 보여라. (힌트: low를 사용하여 분리 정점을 식별하고, edge 스택을 추가하여 다른 DFS를 실행하여 이중 연결 구성 요소를 한 번에 하나씩 제거하라.)