Dao, Tri, and Albert Gu. "Transformers are ssms: Generalized models and efficient algorithms through structured state space duality." arXiv preprint arXiv:2405.21060 (2024).

Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality

Tri Dao** ${ }^{*}$ and Albert Gu* ${ }^{*}$<br>${ }^{1}$ Department of Computer Science, Princeton University<br>${ }^{2}$ Machine Learning Department, Carnegie Mellon University<br>tri@tridao.me, agu@cs.cmu.edu

Abstract

Transformer가 딥러닝의 언어 모델링 성공에 주요 아키텍처였던 반면, Mamba와 같은 **state-space model (SSM)**은 최근 작은 규모에서 중간 규모에 이르기까지 Transformer와 동등하거나 더 나은 성능을 보이는 것으로 나타났다. 우리는 이러한 모델 계열들이 실제로는 매우 밀접하게 관련되어 있음을 보이며, 잘 연구된 structured semiseparable matrix의 다양한 분해를 통해 SSM과 attention 변형 간의 풍부한 이론적 연결 프레임워크를 개발한다. 우리의 state space duality (SSD) 프레임워크는 Mamba의 selective SSM을 개선한 새로운 아키텍처인 Mamba-2를 설계할 수 있게 해주며, 이 핵심 layer는 2~8배 더 빠르면서도 언어 모델링에서 Transformer와 계속해서 경쟁력 있는 성능을 유지한다.

1 Introduction

Transformer, 특히 decoder-only 모델(예: GPT (Brown et al. 2020), Llama (Touvron, Lavril, et al. 2023))은 인과적(causal) 방식으로 입력 시퀀스를 처리하며, 현대 딥러닝 성공의 주요 동력 중 하나이다. 수많은 접근 방식들이 핵심 attention layer의 효율성 문제를 해결하기 위해 이를 근사화하려고 시도한다 (Tay et al. 2022). 이러한 문제로는 학습 시 시퀀스 길이에 대해 제곱으로 증가하는 스케일링과 autoregressive 생성 시 시퀀스 길이에 비례하는 캐시 크기 요구 등이 있다.
이와 병행하여, 대체 시퀀스 모델의 한 종류인 **structured state-space model (SSM)**이 등장했으며, 이들은 학습 시 시퀀스 길이에 대해 선형 스케일링을 보이고 생성 시에는 상수 크기의 state를 유지한다. 이들은 장거리 task(예: S4 (Gu, Goel, and Ré 2022))에서 강력한 성능을 보였으며, 최근에는 작거나 중간 규모의 언어 모델링(예: Mamba (Gu and Dao 2023))에서 Transformer와 동등하거나 더 나은 성능을 달성했다.
그러나 SSM의 개발은 Transformer를 이론적으로 이해하고 현대 하드웨어에서 최적화하는 등 커뮤니티의 공동 노력과는 다소 분리되어 진행되어 왔다. 그 결과, Transformer에 비해 SSM을 이해하고 실험하기가 더 어렵고, 알고리즘 및 시스템 관점에서 Transformer만큼 효율적으로 SSM을 학습시키는 것은 여전히 도전적인 과제이다.

우리의 주요 목표는 structured SSM과 attention 변형들 간의 풍부한 이론적 연결을 개발하는 것이다. 이를 통해 Transformer를 위해 개발된 알고리즘 및 시스템 최적화 기법들을 SSM으로 이전하여, Transformer보다 성능이 우수하면서도 시퀀스 길이에 대해 더 효율적으로 스케일링되는 foundation model을 구축하는 것을 목표로 한다. 이 방향에서 중요한 기여는 Linear Attention (LA) 프레임워크 (Katharopoulos et al. 2020)였다. 이 프레임워크는 quadratic kernelized attention의 "이중 형태(dual forms)"와 특정 선형 재귀(linear recurrence) 간의 등가성을 보여줌으로써 autoregressive attention과 선형 RNN 간의 연결을 도출했다. 이러한 이중성은 효율적인 병렬 학습과 효율적인 autoregressive 추론이라는 새로운 기능을 가능하게 한다. 이와 같은 맥락에서, 본 논문은 선형 복잡도 SSM과 quadratic 복잡도 형태를 연결하는 다양한 관점을 제공하여 SSM과 attention의 강점을 결합한다.

State Space Duality. structured SSM과 attention 변형들을 연결하는 우리의 프레임워크를 **structured state space duality (SSD)**라고 부르며, 이는 structured matrix의 추상화를 통해 이루어진다: 즉, subquadratic 파라미터와 곱셈 복잡도를 가진 행렬이다. 우리는 시퀀스 모델을 표현하기 위한 두 가지 광범위한 프레임워크를 개발하는데, 하나는 **행렬 변환(matrix transformation)**으로, 다른 하나는 **텐서 축약(tensor contraction)**으로 표현하며, 각각은 이중성의 다른 관점을 드러낸다. 우리의 기술적 기여는 다음과 같다:

• 우리는 state space model과 semiseparable matrix라고 불리는 잘 연구된 structured matrix 계열 간의 등가성을 보인다 (Section 3). 이 연결은 우리 프레임워크의 핵심이며, SSM에 대한 새로운 속성과 알고리즘을 밝혀낸다. 본 논문의 핵심 메시지는 state space model을 계산하는 다양한 방법들이 structured matrix에 대한 다양한 행렬 곱셈 알고리즘으로 재구성될 수 있다는 것이다.
• 우리는 Linear Attention (Katharopoulos et al. 2020)의 이론을 크게 개선한다. 먼저 텐서 축약의 언어를 통해 재귀 형태에 대한 통찰력 있는 증명을 제공한 다음, 이를 새로운 structured masked attention (SMA) 계열로 일반화한다 (Section 4).
• 우리는 SSM과 SMA를 연결하여, 이들이 서로의 이중체(dual)인 큰 교집합을 가지고 있음을 보여준다.

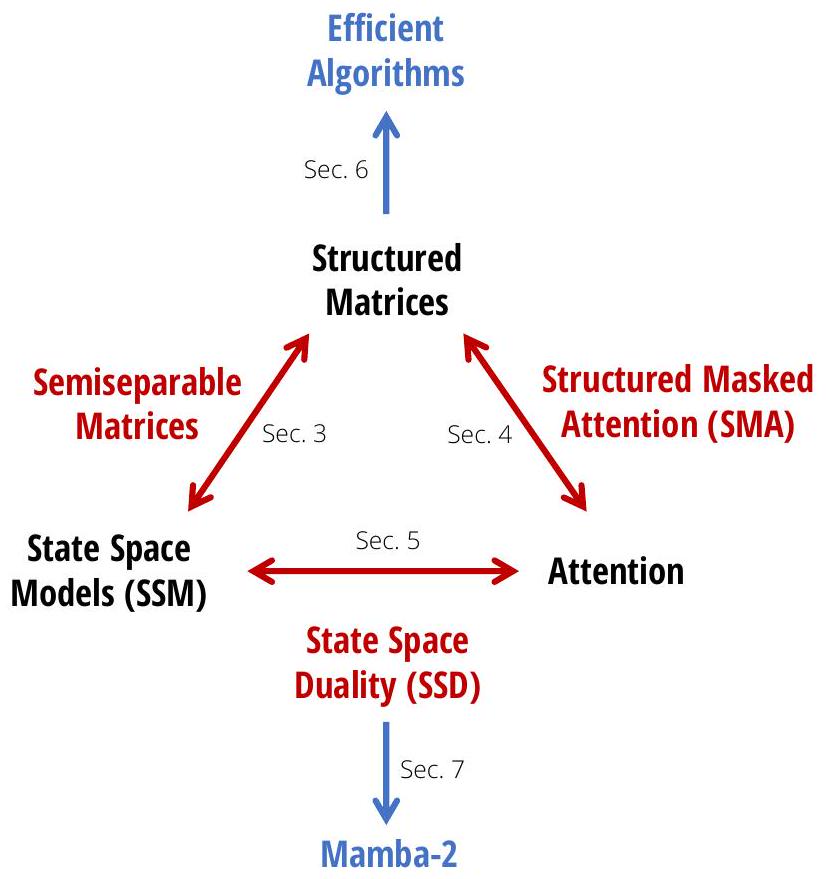
Figure 1: (Structured State-Space Duality.) 본 논문은 structured matrix를 다리 삼아 state space model과 attention 간의 관계를 구체화한다.

본 프레임워크는 본질적인 이론적 가치를 넘어, 시퀀스 모델을 이해하고 개선하기 위한 광범위한 방향을 제시한다.

효율적인 알고리즘 (Efficient Algorithms)
첫째, 그리고 가장 중요하게, 우리 프레임워크는 SSM을 계산하기 위한 새롭고 효율적이며 쉽게 구현 가능한 알고리즘을 제시한다 (Section 6). 우리는 semiseparable matrix의 블록 분해(block decomposition)에 기반한 새로운 SSD 알고리즘을 소개한다. 이 알고리즘은 선형 SSM 재귀와 quadratic 이중 형태를 모두 활용하여, 모든 주요 효율성 축(예: 학습 및 추론 계산, 메모리 사용량, 현대 하드웨어의 행렬 곱셈 유닛 활용 능력)에서 최적의 trade-off를 달성한다. SSD의 전용 구현은 Mamba의 최적화된 selective scan 구현보다 2-8배 빠르며, 동시에 **훨씬 더 큰 재귀 state 크기(Mamba 크기의 8배 이상, 최소한의 속도 저하로)**를 허용한다. SSD는 최적화된 softmax attention 구현(FlashAttention-2 (Dao 2024))과도 매우 경쟁적이며, 시퀀스 길이 2K에서 교차점을 보이고 시퀀스 길이 16K에서는 6배 더 빠르다.

아키텍처 설계 (Architecture Design)
SSM과 같은 새로운 아키텍처를 채택하는 데 주요 장애물 중 하나는 Transformer에 맞춰진 생태계, 즉 대규모 학습을 위한 하드웨어 효율적인 최적화 및 병렬화 기술이다. 우리 프레임워크는 attention에 대한 확립된 관례와 기술을 사용하여 SSM을 위한 아키텍처 설계 선택의 어휘를 구축하고, 이를 더욱 개선할 수 있도록 한다 (Section 7). 예를 들어, 우리는 multi-head attention (MHA)의 head 개념을 SSM에 도입한다. 우리는 Mamba 아키텍처가 multi-input SSM (MIS)이며, 이는 multi-value attention (MVA)과 유사하다는 것을 보여주고, 다른 head 구조를 가진 Mamba의 다른 변형들을 비교한다.

우리는 또한 이러한 아이디어를 사용하여 Mamba 블록에 약간의 수정을 가했으며, 이를 통해 텐서 병렬화(tensor parallelism)를 구현할 수 있게 되었다 (예: Megatron (Shoeybi et al. 2019) 방식). 주요 아이디어는 grouped-value attention (GVA) head 구조를 도입하고, 모든 데이터 종속적인 projection을 블록 시작 부분에서 병렬로 발생하도록 이동시키는 것이다.

수정된 병렬 Mamba 블록과 SSD를 내부 SSM layer로 사용하는 조합은 Mamba-2 아키텍처를 탄생시킨다. 우리는 Mamba와 동일한 설정에서 Mamba-2에 대한 Chinchilla scaling law를 조사했으며, perplexity와 wall-clock time 모두에서 Mamba와 Transformer++를 Pareto 지배한다는 것을 발견했다. 또한, 우리는 Pile 데이터셋에서 다양한 크기의 Mamba-2 모델 계열을 학습시켰으며, 이는 표준 다운스트림 평가에서 Mamba 및 오픈 소스 Transformer와 동등하거나 더 나은 성능을 보인다. 예를 들어, Pile 데이터셋에서 300B 토큰으로 학습된 2.7B 파라미터의 Mamba-2는 Mamba-2.8B, Pythia-2.8B, 심지어 Pythia-6.9B보다 더 나은 성능을 보인다.

시스템 최적화 (Systems Optimizations)
SSD 프레임워크는 SSM과 Transformer를 연결하여, Transformer를 위해 개발된 풍부한 시스템 최적화 연구를 활용할 수 있게 한다 (Section 8).

• 예를 들어, **Tensor Parallelism (TP)**은 동일 노드의 GPU에 걸쳐 각 layer를 분할하여 대규모 Transformer 모델을 학습시키는 중요한 모델 병렬화 기술이다. 우리는 Mamba-2를 TP 친화적으로 설계하여, 블록당 동기화 지점 수를 절반으로 줄였다.
• 활성화(activation)가 단일 장치에 맞지 않는 매우 긴 시퀀스의 경우, attention 블록을 위한 시퀀스 병렬화(sequence parallelism)가 개발되었다. 우리는 재귀 state를 장치 간에 전달함으로써 SSM 전반과 특히 Mamba-2를 시퀀스 병렬화로 학습시키는 방법을 설명한다.
• 길이가 다른 예시로 fine-tuning할 때, 최고의 효율성을 위해 Transformer는 패딩 토큰을 제거하고 가변 길이 시퀀스에 attention을 수행하는 정교한 기술이 필요하다. 우리는 Mamba-2가 패딩 토큰 없이 가변 시퀀스 길이로 효율적으로 학습될 수 있음을 보여준다.

Section 9에서는 언어 모델링, 학습 효율성, 그리고 어려운 multi-query associative recall task (Arora, Eyuboglu, Zhang, et al. 2024)에 대한 Mamba-2의 성능을 경험적으로 검증한다. 마지막으로, Section 10에서는 확장된 관련 연구를 제공하고 우리 프레임워크가 열어주는 잠재적인 연구 방향을 논의한다.

모델 코드와 사전학습된 체크포인트는 https://github.com/state-spaces/mamba에서 오픈 소스로 공개되어 있다.

2 Background and Overview

2.1 Structured State Space Models

Structured state space sequence model (S4)는 RNN, CNN, 그리고 고전적인 state space model과 폭넓게 연관된 딥러닝용 시퀀스 모델의 최신 클래스이다. 이들은 1차원 시퀀스 $x \in \mathbb{R}^{\top} \mapsto y \in \mathbb{R}^{\top}$를 암묵적인 잠재 상태 $h \in \mathbb{R}^{(\top, N)}$를 통해 매핑하는 특정 연속 시스템 (1)에서 영감을 받았다.

구조화된 SSM의 일반적인 이산 형태는 방정식 (1)의 형태를 취한다.

$$\begin{aligned} & h_{t}=A h_{t-1}+B x_{t} \\ & y_{t}=C^{\top} h_{t} \end{aligned}$$ $$\begin{aligned} & h_{t}=A_{t} h_{t-1}+B_{t} x_{t} \\ & y_{t}=C_{t}^{\top} h_{t} \end{aligned}$$

여기서 $A \in \mathbb{R}^{(\mathrm{N}, \mathrm{N})}, B \in \mathbb{R}^{(\mathrm{N}, 1)}, C \in \mathbb{R}^{(\mathrm{N}, 1)}$이다. 구조화된 SSM은 시간 역학을 제어하는 $A$ 행렬이 딥 뉴럴 네트워크에서 사용될 만큼 충분히 효율적으로 시퀀스-투-시퀀스 변환을 계산하기 위해 구조화되어야 하기 때문에 그렇게 명명되었다. 처음 도입된 구조는 diagonal plus low-rank (DPLR) (Gu, Goel, and Ré 2022)와 diagonal (Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; J. T. Smith, Warrington, and Linderman 2023)이었으며, 이는 여전히 가장 인기 있는 구조이다.

본 연구에서는 **state space model (SSM)**이라는 용어를 구조화된 SSM을 지칭하는 데 사용한다. 이러한 SSM에는 continuous-time, recurrent, convolutional model과 같은 여러 주요 신경 시퀀스 모델 패러다임과 깊은 연관성을 가진 다양한 종류가 있다 (Gu, Johnson, Goel, et al. 2021). 아래에서 간략한 개요를 제공하며, 더 많은 맥락과 세부 사항은 이전 연구를 참조한다 (Gu 2023; Gu and Dao 2023).

Continuous-time Models. 원래의 구조화된 SSM은 시퀀스에 직접 작동하기보다는 함수 $x(t) \in \mathbb{R} \mapsto y(t) \in \mathbb{R}$에 대한 continuous-time map으로 시작되었다. continuous-time 관점에서, 방정식 (1a)에서 행렬 ($A, B$)은 직접 학습되지 않고 기본 파라미터 ($\stackrel{\circ}{A}, \stackrel{\circ}{B}$)와 파라미터화된 스텝 크기 $\Delta$로부터 생성된다. "continuous parameters" ($\Delta, \stackrel{\circ}{A}, \stackrel{\circ}{B}$)는 고정된 공식 $A=f_{A}(\Delta, \stackrel{\circ}{A})$ 및 $B=f_{B}(\Delta, \stackrel{\circ}{B})$를 통해 "discrete parameters" ($A, B$)로 변환되며, 여기서 쌍 ($f_{A}, f_{B}$)은 discretization rule이라고 불린다.

Remark 1. 우리의 주요 모델은 이전 연구와 동일한 파라미터화 및 이산화 단계를 채택하지만 (자세한 내용은 Gu and Dao (2023) 참조), 설명을 단순화하기 위해 본 논문의 나머지 부분에서는 이를 생략한다. 구조화된 SSM에 대한 이전 연구에서는 continuous parameters $(\dot{A}, \stackrel{\circ}{B})$와 discrete parameters $(A, B)$를 각각 $(A, B)$와 $(\bar{A}, \bar{B})$로 지칭했음을 언급한다. 우리는 표기법을 변경하여 표현을 단순화하고, 주요 SSM 재귀를 제어하는 discrete parameters에 직접 초점을 맞추었다.

Recurrent Models. 방정식 (1)과 (2)는 입력 $x$에 대해 선형인 재귀 형태를 취한다. 따라서 구조화된 SSM은 RNN의 한 유형으로 볼 수 있으며, 선형성은 추가적인 속성을 부여하고 전통적인 RNN의 순차적 계산을 피할 수 있게 한다. 반대로, 이러한 단순화에도 불구하고 SSM은 시퀀스 변환으로서 여전히 완전한 표현력을 가진다 (universal approximation의 의미에서) (Kaul 2020; Orvieto et al. 2023; Shida Wang and Xue 2023).

Convolutional Models. SSM의 동역학이 방정식 (1)에서처럼 시간에 따라 일정할 때, 이 모델은 **linear time-invariant (LTI)**라고 불린다. 이 경우, 이들은 convolution과 동등하다. 따라서 SSM은 CNN의 한 유형으로도 볼 수 있지만, (i) convolution kernel이 SSM 파라미터 ($A, B, C$)를 통해 암묵적으로 파라미터화되고 (ii) convolution kernel이 일반적으로 local이 아닌 global이라는 차이가 있다. 반대로, 고전적인 신호 처리 이론을 통해 모든 충분히 잘 동작하는 convolution은 SSM으로 표현될 수 있다.

일반적으로 이전 LTI SSM은 효율적인 병렬 학습(전체 입력 시퀀스를 미리 볼 수 있는 경우)을 위해 convolutional mode를 사용하고, 효율적인 autoregressive inference(입력이 한 번에 한 단계씩 보이는 경우)를 위해 recurrent mode (1)로 전환한다.

Selective State Space Models. 파라미터 ($A, B, C$)가 시간적으로도 변할 수 있는 형태 (2)는 Mamba에서 selective SSM으로 도입되었다. 표준 LTI 공식 (1)과 비교하여, 이 모델은 모든 타임스텝에서 입력을 선택적으로 집중하거나 무시할 수 있다. 특히 언어와 같이 정보 밀도가 높은 데이터에서 LTI SSM보다 훨씬 더 나은 성능을 보였으며, 이는 상태 크기 N이 증가하여 더 많은 정보 용량을 허용하기 때문이다. 그러나 이 모델은 convolutional mode 대신 recurrent mode로만 계산될 수 있으며, 효율성을 위해 신중한 하드웨어 인식 구현이 필요하다. 그럼에도 불구하고, GPU 및 TPU와 같은 최신 가속기가 전문화된 행렬 곱셈 단위를 활용하지 않기 때문에 CNN 및 Transformer와 같은 하드웨어 친화적인 모델보다 효율성이 떨어진다.

시간 불변 SSM은 continuous, recurrent, convolutional 시퀀스 모델과 밀접하게 관련되어 있지만, attention과는 직접적인 관련이 없다. 본 논문에서는 selective SSM과 attention 간의 더 깊은 관계를 보여주고, 이를 사용하여 SSM의 학습 속도를 크게 향상시키는 동시에 훨씬 더 큰 상태 크기 N을 허용한다.

Structured SSMs as Sequence Transformations.

정의 2.1. 우리는 **시퀀스 변환(sequence transformation)**이라는 용어를 **시퀀스 $Y=f_{\theta}(X)$에 대한 매개변수화된 맵(parameterized map)**을 지칭하는 데 사용한다. 여기서 $X, Y \in \mathbb{R}^{(\mathrm{T}, \mathrm{P})}$이고 $\theta$는 임의의 매개변수 집합이다. T는 시퀀스 또는 시간 축을 나타내며, 아래첨자는 첫 번째 차원을 인덱싱한다. 예를 들어 $X_{t}, Y_{t} \in \mathbb{R}^{\mathrm{P}}$이다.

시퀀스 변환(예: SSM, 또는 self-attention)은 딥 시퀀스 모델의 핵심 요소이며, 이들은 신경망 아키텍처(예: Transformer)에 통합된다. (1) 또는 (2)의 SSM은 $P=1$인 시퀀스 변환이다. 이는 단순히 이 차원에 걸쳐 브로드캐스팅(broadcasting)함으로써 $P>1$로 일반화될 수 있다 (즉, 입력을 P개의 독립적인 시퀀스로 보고 각 시퀀스에 SSM을 적용하는 방식). P는 head dimension으로 생각할 수 있으며, 이에 대해서는 Section 7에서 자세히 설명할 것이다.

정의 2.2. 우리는 **SSM 연산자 $\operatorname{SSM}(A, B, C)=\operatorname{SSM}\left(A_{0: T}, B_{0: T}, C_{0: T}\right)$**를 **방정식 (2)로 정의되는 시퀀스 변환 $X \in \mathbb{R}^{(\mathrm{T}, \mathrm{P})} \mapsto Y \in \mathbb{R}^{(\mathrm{T}, \mathrm{P})}$**로 정의한다.

SSM에서 N 차원은 state size 또는 state dimension이라고 불리는 자유 매개변수이다. 우리는 또한 이를 state expansion factor라고 부르는데, 이는 입력/출력의 크기를 N배로 확장시키며, 이 모델들의 계산 효율성에 영향을 미치기 때문이다.

마지막으로, attention과 같은 많은 유형의 시퀀스 변환은 시퀀스 차원에 걸친 단일 행렬 곱셈으로 표현될 수 있음을 언급한다.

정의 2.3. 우리는 시퀀스 변환 $Y=f_{\theta}(X)$가 $Y=M_{\theta} X$ 형태로 작성될 수 있을 때 이를 **행렬 변환(matrix transformation)**이라고 부른다. 여기서 $M$은 매개변수 $\theta$에 의존하는 행렬이다. 우리는 시퀀스 변환을 행렬 $M$과 동일시하며, 문맥상 명확할 경우 $\theta$에 대한 의존성을 종종 생략한다.

2.2 Attention

Attention은 시퀀스 내의 모든 위치 쌍에 점수를 할당하여 각 요소가 나머지 요소에 "attend"할 수 있도록 하는 계산 유형을 광범위하게 지칭한다. 현재까지 가장 일반적이고 중요한 attention 변형은 softmax self-attention이며, 이는 다음과 같이 정의할 수 있다:

$$Y=\operatorname{softmax}\left(Q K^{\top}\right) \cdot V$$

여기서 $Q, K, V \in \mathbb{R}^{(\mathrm{T}, \mathrm{P})}$이다. 쌍별 비교 메커니즘($Q K^{\top}$를 구체화함으로써 유도됨)은 attention의 특징적인 quadratic training cost를 발생시킨다.

다양한 attention 변형이 제안되었지만, 모두 이러한 attention 점수의 근본적인 핵심을 공유하며, 다양한 근사치를 사용한다 (Tay et al. 2022). 본 연구에서 가장 중요한 변형은 linear attention이다 (Katharopoulos et al. 2020). 대략적으로 말하면, 이 방법군은 softmax를 kernel feature map으로 통합하여 제거하고, 행렬 곱셈의 결합 법칙을 사용하여 $\left(Q K^{\top}\right) \cdot V=Q \cdot\left(K^{\top} V\right)$로 재작성한다. 또한, 중요한 causal (autoregressive) attention의 경우, causal mask가 좌변에 $\left(L \circ Q K^{\top}\right) \cdot V$로 통합될 때 (여기서 $L$은 하삼각 1 행렬), 우변이 recurrence로 확장될 수 있음을 보여준다. RetNet (Y. Sun et al. 2023) 및 GateLoop (Katsch 2023)와 같은 여러 최근 및 동시 연구들은 이를 더 일반적인 형태의 $L$로 강화한다 (Section 10). 본 연구에서 우리의 structured masked attention 공식화는 이러한 아이디어를 강력하게 일반화할 것이다.

2.3 Structured Matrices

일반적인 행렬 $M \in \mathbb{R}^{(\mathrm{T}, \mathrm{T})}$은 $\mathrm{T}^{2}$개의 파라미터를 필요로 하며, 행렬-벡터 곱셈과 같은 기본 연산에 $O\left(\mathrm{~T}^{2}\right)$ 시간이 소요된다. **구조화된 행렬(Structured matrices)**은 다음과 같은 특징을 가진다: (i) 압축된 표현을 통해 준2차(subquadratic, 이상적으로는 선형) 파라미터로 표현될 수 있으며, (ii) 이 압축된 표현에 직접 연산함으로써 **빠른 알고리즘(가장 중요하게는 행렬 곱셈)**을 가질 수 있다.

아마도 가장 대표적인 구조화된 행렬의 종류는 **희소 행렬(sparse matrices)**과 **저랭크 행렬(low-rank matrices)**일 것이다. 그러나 Toeplitz, Cauchy, Vandermonde, butterfly 행렬과 같이 머신러닝에서 효율적인 모델을 위해 사용되어 온 다른 많은 종류의 행렬들도 존재한다 (Dao, Gu, et al. 2019; D. Fu et al. 2024; Gu, Gupta, et al. 2022; Thomas et al. 2018). 구조화된 행렬은 효율적인 표현과 알고리즘을 위한 강력한 추상화이다. 본 연구에서는 SSM이 이전에 딥러닝에서 사용되지 않았던 또 다른 종류의 구조화된 행렬과 동등함을 보이고, 이 연결을 활용하여 효율적인 방법과 알고리즘을 도출할 것이다.

2.4 Overview: Structured State Space Duality

본 논문은 SSM, attention, 그리고 구조화된 행렬 간의 훨씬 더 풍부한 연결 프레임워크를 개발하지만, 여기서는 주요 방법론에 대한 간략한 요약을 제공한다. 이 방법론은 실제로는 매우 독립적이고 알고리즘적으로도 간단하다.

Recurrent (Linear) Form.
State Space Dual (SSD) layer는 selective SSM (2)의 특수한 경우로 정의될 수 있다. SSM의 표준 계산 방식인 **recurrence (또는 parallel scan)**를 적용할 수 있으며, 이는 시퀀스 길이에 대해 선형적인 복잡도를 가진다. Mamba에서 사용된 버전과 비교할 때, SSD는 두 가지 사소한 차이점을 가진다:

• $A$의 구조가 대각선(diagonal)에서 스칼라 곱하기 항등 행렬(scalar times identity) 구조로 더욱 단순화되었다. 이 경우 각 $A_t$는 단순히 스칼라로 식별될 수 있다.
• Mamba에서 사용된 $\mathrm{P}=1$에 비해 더 큰 head dimension P를 사용한다. 일반적으로 **$\mathrm{P}=\{64, 128\}$**이 선택되는데, 이는 최신 Transformer의 관례와 유사하다.

원래의 selective SSM과 비교할 때, 이러한 변경 사항은 표현력(expressive power)을 약간 감소시키는 대신 상당한 학습 효율성 개선을 가져온 것으로 볼 수 있다. 특히, 우리의 새로운 알고리즘은 최신 가속기에서 행렬 곱셈 유닛(matrix multiplication units)의 사용을 가능하게 한다.

Dual (Quadratic) Form.
SSD의 dual form은 attention과 밀접하게 관련된 quadratic 계산이며, 다음과 같이 정의된다:

$$\left(L \circ Q K^{\top}\right) \cdot V \quad L_{i j}= \begin{cases}a_{i} \times \cdots \times a_{j+1} & i \geq j \\ 0 & i<j\end{cases}$$

여기서 $a_i$는 $[0,1]$ 범위에 있는 **입력 의존적인 스칼라(input-dependent scalars)**이다.
표준 softmax attention과 비교할 때, 두 가지 주요 차이점이 있다:

• softmax가 제거되었다.
• attention 행렬은 추가적인 마스크 행렬 $L$과 element-wise로 곱해진다.

이 두 가지 변경 사항은 바닐라 attention의 문제점을 해결하는 것으로 볼 수 있다. 예를 들어, softmax는 최근 "attention sink" 현상(Darcet et al. 2024; Xiao et al. 2024)과 같이 attention score에 문제를 일으키는 것으로 관찰되었다. 더 중요한 것은, 마스크 행렬 $L$이 Transformer의 휴리스틱한 positional embedding을 대체하여, 시간에 따라 정보가 얼마나 전달되는지를 제어하는 다른 데이터 의존적인 positional mask로 볼 수 있다는 점이다.

더 넓게 보면, 이 형태는 Section 4에서 정의된 선형 attention의 구조화된 마스크 attention 일반화의 한 예시이다.

Matrix Form and SSD Algorithm.
SSD의 다양한 형태는 통합된 행렬 표현을 통해 연결된다. 이는 SSM이 $\theta=(A, B, C)$에 의존하는 행렬 $M_{\theta} \in \mathbb{R}^{(\mathrm{T}, \mathrm{T})}$에 대한 행렬 변환 형태 $Y=M X$를 가진다는 것을 보여줌으로써 이루어진다. 특히, SSD의 dual form은 행렬 $M$에 대한 naive (quadratic-time) 곱셈과 동등하며, recurrent form은 $M$의 구조를 활용하는 특정 효율적인 (linear-time) 알고리즘이다.

이러한 것들을 넘어, $M$에 대한 곱셈을 위한 어떤 알고리즘이든 적용될 수 있다. 우리가 제안하는 하드웨어 효율적인 SSD 알고리즘(Section 6)은 $M$의 블록 분해(block decompositions)를 포함하는 새로운 구조화된 행렬 곱셈 방법으로, 순수 선형 또는 quadratic 형태보다 더 나은 효율성 trade-off를 얻는다. 이는 일반적인 selective SSM (Gu and Dao 2023)에 비해 상대적으로 간단하고 구현하기 쉽다. Listing 1은 몇 줄의 코드로 완전한 구현을 제공한다.

Figure 1은 본 논문에서 제시된 개념들 간의 관계에 대한 간단한 로드맵을 제공한다.

2.5 Notation

본 논문 전반에 걸쳐 우리는 코드에 직접 매핑될 수 있는 정확한 표기법을 사용하고자 한다.

행렬 및 벡터 (Matrices and Vectors)
우리는 일반적으로 **벡터(단일 축을 가진 텐서)**를 나타낼 때는 소문자를 사용하고, **행렬(두 개 이상의 축을 가진 텐서)**을 나타낼 때는 대문자를 사용한다. 본 연구에서는 행렬을 굵게 표시하지 않는다. 때때로 행렬이 한 축을 따라 묶여 있거나 반복되는 경우(따라서 벡터로도 볼 수 있는 경우), 대문자 또는 소문자를 사용할 수 있다. ${ }^{2}$는 스칼라 또는 행렬 곱셈을 나타내며, $\circ$는 Hadamard (요소별) 곱셈을 나타낸다.

인덱싱 (Indexing)
우리는 Python 스타일의 인덱싱을 사용한다. 예를 들어, $i:j$는 $i<j$일 때 $(i, i+1, \ldots, j-1)$ 범위를, $i>j$일 때 $(i, i-1, \ldots, j+1)$ 범위를 나타낸다. 예를 들어, 임의의 기호 $v$에 대해 $j \geq i$인 $v_{j:i}$는 시퀀스 $(v_j, \ldots, v_{i+1})$를 나타낸다. $[i]$는 $0:i=(0, \ldots, i-1)$와 동일하다. 줄임말로, $v_{j:i}^{\times}$는 곱 $v_j \times \cdots \times v_{i+1}$을 나타낸다.

차원 (Dimensions)
행렬 및 텐서와 구별하기 위해, 우리는 종종 **타자기 글꼴의 대문자(예: D, N, T)**를 사용하여 **차원(dimension) 및 텐서의 형태(shape)**를 나타낸다. 전통적인 표기법 $M \in \mathbb{R}^{T \times T}$ 대신, 우리는 코드의 텐서 형태를 반영하기 위해 **$M \in \mathbb{R}^{(\mathrm{T}, \mathrm{T})}$**를 자주 사용한다.

텐서 축약 (Tensor Contractions)
우리는 명확성을 위해, 그리고 결과 진술 및 증명의 핵심 도구로서 텐서 축약(tensor contraction) 또는 einsum 표기법에 크게 의존할 것이다. 우리는 독자들이 이 표기법에 익숙하다고 가정하며, 이 표기법은 numpy와 같은 최신 텐서 라이브러리에서 일반적으로 사용된다. 예를 들어, 행렬-행렬 곱셈 연산자를 나타내기 위해 contract($\mathrm{MN}, \mathrm{NK} \rightarrow \mathrm{MK}$)를 사용할 수 있으며, 우리의 표기법에서 contract($\mathrm{MN}, \mathrm{NK} \rightarrow \mathrm{MK}$) ($X, Y$) (이는 $X \cdot Y$와 동일하다)는 코드에서 numpy.einsum('mn, nk $\rightarrow \mathrm{mk}^{\prime}, \mathrm{X}, \mathrm{Y}$)로 번역될 수 있다.

표기법에 대한 광범위한 용어집은 Appendix A에 포함되어 있다.

3 State Space Models are Structured Matrices

이 섹션에서는 state space model을 **시퀀스 변환(sequence transformation)**의 다양한 관점에서 탐구하고, 이러한 맵의 속성 및 알고리즘을 설명한다. 이 섹션의 주요 결과는 **state space model과 semiseparable matrices라는 구조화된 행렬 계열 간의 등가성(equivalence)**에 관한 것이며, 이는 새로운 효율성 결과(정리 3.5 및 3.7)를 함의한다.

3.1 The Matrix Transformation Form of State Space Models

SSM의 정의는 (2)를 통해 정의된 parameterized map임을 상기하자. 우리의 이론적 프레임워크는 이 변환을 벡터 $x \in \mathbb{R}^{\top} \mapsto y \in \mathbb{R}^{\top}$를 매핑하는 행렬 곱셈으로 간단히 표현하는 것에서 시작한다.

정의에 따라 $h_0 = B_0 x_0$이다. 귀납적으로,

$$\begin{aligned} h_{t} & =A_{t} \ldots A_{1} B_{0} x_{0}+A_{t} \ldots A_{2} B_{1} x_{1}+\cdots+A_{t} A_{t-1} B_{t-2} x_{t-2}+A_{t} B_{t-1} x_{t-1}+B_{t} x_{t} \\ & =\sum_{s=0}^{t} A_{t: s}^{\times} B_{s} x_{s} . \end{aligned}$$

$y_t$를 생성하기 위해 $C_t$를 곱하고, $t \in [\mathrm{T}]$에 대해 방정식을 벡터화하면, SSM의 행렬 변환 형태를 도출할 수 있다.

$$\begin{aligned} y_{t} & =\sum_{s=0}^{t} C_{t}^{\top} A_{t: s}^{\times} B_{s} x_{s} \\ y & =\operatorname{SSM}(A, B, C)(x)=M x \\ M_{j i} & :=C_{j}^{\top} A_{j} \cdots A_{i+1} B_{i} \end{aligned}$$

3.2 Semiseparable Matrices

Equation (3)의 $M$은 semiseparable matrix로 알려진 특정 클래스의 행렬 표현이다. Semiseparable matrix는 기본적인 행렬 구조이다. 우리는 먼저 이 행렬들과 그 속성을 정의한다.

정의 3.1. (하삼각) 행렬 $M$이 N-semiseparable이라는 것은 하삼각 부분(즉, 대각선 상 또는 아래)에 포함된 모든 부분행렬의 rank가 최대 N이라는 의미이다. 여기서 N을 semiseparable matrix의 order 또는 rank라고 부른다.

정의 3.1과 이와 관련된 다른 형태의 "separable" 구조(예: quasiseparable matrix 및 semiseparable matrix의 다른 정의)는 structured rank matrix (또는 rank-structured matrix)라고 불리기도 한다. 이는 부분행렬의 rank 조건으로 특징지어지기 때문이다. Semiseparable matrix는 hierarchical semiseparable (HSS), sequential semiseparable (SSS), Bruhat form (Pernet and Storjohann 2018)을 포함한 많은 구조화된 표현을 가진다. 우리는 주로 SSS form을 사용할 것이다.

3.2.1 The Sequentially Semiseparable (SSS) Representation

정의 3.2. 하삼각 행렬 $M \in \mathbb{R}^{(T, T)}$은 다음 형태로 표현될 수 있다면 $N$-sequentially semiseparable (SSS) representation을 가진다.

$$M_{j i}=C_{j}^{\top} A_{j} \cdots A_{i+1} B_{i}$$

여기서 벡터 $B_{0}, \ldots, B_{\mathrm{T}-1}, C_{0}, \ldots, C_{\mathrm{T}-1} \in \mathbb{R}^{\mathrm{N}}$ 및 행렬 $A_{0}, \ldots, A_{\mathrm{T}-1} \in \mathbb{R}^{(\mathrm{N}, \mathrm{N})}$이다. 우리는 연산자 SSS를 $M=\operatorname{SSS}\left(A_{0: \mathrm{T}}, B_{0: \mathrm{T}}, C_{0: \mathrm{T}}\right)$로 정의한다.

semiseparable 행렬의 근본적인 결과는 SSS representation을 가진 행렬과 정확히 동등하다는 것이다. 한 방향은 간단한 구성적 증명으로 유추할 수 있다.

보조정리 3.3. 표현 (4)를 가진 $N$-SSS 행렬 $M$은 $N$-semiseparable이다. 증명. $j^{\prime}>j \geq i>i^{\prime}$인 임의의 비대각 블록 $M_{j: j^{\prime}, i^{\prime}: i}$를 고려하자. 이는 다음과 같이 명시적인 rank-$N$ factorization을 가진다.

$$\left[\begin{array}{ccc} C_{j}^{\top} A_{j: i^{\prime}}^{\times} B_{i^{\prime}} & \cdots & C_{j}^{\top} A_{j: i-1}^{\times} B_{i-1} \\ \vdots & & \vdots \\ C_{j^{\prime}-1}^{\top} A_{j^{\prime}-1: i^{\prime}}^{\times} B_{i^{\prime}} & \cdots & C_{j^{\prime}-1}^{\top} A_{j^{\prime}-1: i-1}^{\times} B_{i-1} \end{array}\right]=\left[\begin{array}{c} C_{j}^{\top} A_{j: j}^{\times} \\ \vdots \\ C_{j^{\prime}-1}^{\top} A_{j^{\prime}-1: j}^{\times} \end{array}\right] A_{j: i-1}^{\times}\left[\begin{array}{lll} \times & & \\ \times 1: i^{\prime} & B_{i^{\prime}} & \cdots \\ A_{i-1: i-1}^{\times} B_{i-1} \end{array}\right]$$

Equation (5)는 시퀀스 모델을 위한 고속 알고리즘을 도출하는 데 광범위하게 사용될 것이다. 다른 방향은 semiseparable 행렬에 대한 문헌에서 잘 확립되어 있다. 명제 3.4. 모든 $N$-semiseparable 행렬은 $N$-SSS representation을 가진다. 또한, 정의 3.2는 representation을 위해 $O\left(\mathrm{~N}^{2} \mathrm{~T}\right)$개의 파라미터를 포함하지만 (특히 $A$ 행렬을 저장하기 위해), 실제로는 $O(\mathrm{NT})$개의 파라미터로 압축될 수 있으며, 이는 점근적으로 타이트하다 (Pernet, Signargout, and Villard 2023). 따라서 본 논문의 나머지 부분에서는 구조화된 행렬 클래스(정의 3.1)와 그 특정 representation(정의 3.2)을 혼용할 것이다. 우리는 항상 다른 후보 대신 이 representation을 사용할 것이다. 결과적으로 우리는 SSS 형태의 $N$-semiseparable 행렬을 지칭하기 위해 $N$-SS를 사용할 것이다.

semiseparable 행렬은 근본적인 행렬 구조이며 많은 중요한 속성을 가지고 있다. 이들은 일반적인 recurrence와 깊이 관련되어 있으며, 다양한 특성화(예: 정의 3.1 및 3.2)를 통해 정의될 수 있으며, 이는 이들에 대한 다양한 연결과 효율적인 알고리즘을 보여준다. 우리는 Appendix C.1에서 이들의 다른 속성 중 일부를 언급한다. 비고 2. semiseparability의 개념은 매우 광범위하며 문헌에는 유사하지만 미묘하게 다른 많은 정의가 나타난다. 우리의 정의는 다른 관례와 약간 다를 수 있다. 첫째, 본 논문에서는 주로 causal 또는 autoregressive 설정에 초점을 맞추고 있기 때문에, semiseparability의 정의를 삼각 행렬의 경우로 제한했다. 정의 3.1은 일부 저자들에 의해 더 공식적으로 ($N, 0$)-semiseparability라고 불릴 수 있다. 일부 저자들은 이를 quasiseparability의 한 형태로 언급할 수도 있다 (Eidelman and Gohberg 1999; Pernet 2016). 간략한 조사는 Vandebril et al. (2005)를 참조하라.

3.2.2 1-Semiseparable Matrices: the Scalar SSM Recurrence

우리는 1-SS 행렬이라는 특수한 경우를 다룰 것이다. 이 경우 $C_j$와 $B_i$는 스칼라(scalar)이며, SSS 표현 (4)에서 인수분해(factor out)될 수 있다 (이 경우 파라미터가 스칼라임을 강조하기 위해 소문자를 사용한다).

$$\operatorname{SSS}(a, b, c)=\operatorname{diag}(c) \cdot M \cdot \operatorname{diag}(b) \quad \text { where } \quad M_{j i}=a_{j: i}^{\times}$$

대각 행렬(diagonal matrix)은 다루기 쉽기 때문에(예: 대각 행렬과의 곱셈은 원소별 스칼라 곱셈과 동일), 이 항들은 무시할 수 있다. 따라서 1-SS 행렬의 기본 표현은 $M_{j i}=a_{j: i}$ 또는 다음과 같다.

$$M=1 \operatorname{SS}\left(a_{0: T}\right):=\left[\begin{array}{ccccc} 1 & & & & \\ a_{1} & 1 & & & \\ a_{2} a_{1} & a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ a_{T-1} \ldots a_{1} & a_{T-1} \ldots a_{2} & \ldots & a_{T-1} & 1 \end{array}\right]$$

1-SS 행렬의 중요성은 스칼라 recurrence의 최소 형태(minimal form)와 동등하다는 점에 있다. 이는 상태 차원(state dimension) N=1이고 (B, C) projection이 없는 퇴화된(degenerate) SSM의 경우에 해당한다. 곱셈 $y=Mx$는 다음 recurrence로 계산될 수 있다.

$$\begin{aligned} y_{t} & =a_{t: 0} x_{0}+\cdots+a_{t: t} x_{t} \\ & =a_{t}\left(a_{t-1: 0} x_{0}+\cdots+a_{t-1: t-1} x_{t-1}\right)+a_{t: t} x_{t} \\ & =a_{t} y_{t-1}+x_{t} \end{aligned}$$

Figure 2: (State Space Model은 Semiseparable 행렬이다.) 시퀀스 변환으로서, State Space Model은 시퀀스 차원 T에 작용하는 행렬 변환 $M \in \mathbb{R}^{(T, T)}$으로 표현될 수 있으며, 각 채널에 대해 동일한 행렬을 공유한다 (왼쪽). 이 행렬은 semiseparable 행렬이다 (오른쪽). semiseparable 행렬은 rank-structured 행렬로, 대각선 위 또는 아래에 포함된 모든 부분 행렬(파란색)의 rank가 SSM의 상태 차원 N과 같거나 그보다 작다.

따라서 우리는 1-SS 행렬에 의한 행렬 곱셈을 스칼라 SSM recurrence 또는 cumprodsum (cumulative product sum; 누적 곱과 누적 합의 일반화) 연산자라고도 부른다. recurrence의 근본적인 형태로서, 1-SS 행렬에 의한 곱셈은 우리의 주요 알고리즘을 구성하는 빌딩 블록으로서 중요하다.

본 논문의 핵심 주제 중 하나는 시퀀스 모델에 대한 많은 알고리즘이 구조화된 행렬 곱셈 알고리즘으로 환원될 수 있다는 점을 강조한다. 1-SS 행렬은 이러한 연결을 잘 보여준다: 기본적인 스칼라 recurrence 또는 cumprodsum 연산자를 계산하기 위한 많은 빠른 알고리즘이 있으며, 이들 모두는 1-SS 행렬의 서로 다른 구조화된 인수분해와 동등함이 밝혀졌다. 우리는 Appendix B에서 1-SS 행렬 곱셈을 위한 이러한 알고리즘들을 다룬다.

3.3 State Space Models are Semiseparable Matrices

우리의 SSM 정의는 정의 2.1을 통해 정의된 parameterized map임을 상기하라. SSM과 semiseparable matrix 간의 연결은 이 변환을 벡터 $x \mapsto y \in \mathbb{R}^{\top}$를 매핑하는 행렬 곱셈으로 간단히 표현함으로써 얻어진다.

**Equation (3)**은 state space model과 sequentially semiseparable representation 간의 직접적인 연결을 설정하며, 이는 다시 일반적으로 semiseparable matrix와 동등하다 (Lemma 3.3 및 Proposition 3.4).

Theorem 3.5. state size N을 갖는 state space model transformation $y=\operatorname{SSM}(A, B, C)(x)$는 sequentially semiseparable representation $y=\operatorname{SSS}(A, B, C) \cdot x$에서 N-SS matrix에 의한 행렬 곱셈과 동일하다.

다시 말해, **sequence transformation operator SSM (정의 2.2)**은 **matrix construction operator SSS (정의 3.2)**와 일치하며, 우리는 이들을 상호 교환적으로 사용한다 (때로는 SS를 약어로 사용하기도 한다). 더욱이, 우연의 일치로 structured state space model과 sequentially semiseparable matrix는 동일한 약어를 가지며, 이는 그들의 동등성을 강조한다! 편리하게도 우리는 이들 약어 SSM (state space model 또는 semiseparable matrix), SSS (structured state space 또는 sequentially semiseparable), 또는 SS (state space 또는 semiseparable) 중 어느 것을 사용하더라도 두 개념을 명확하게 지칭할 수 있다. 그러나 일반적으로 SSM은 state space model을, SS는 semiseparable을, SSS는 sequentially semiseparable을 지칭하는 관례를 따를 것이다.

Figure 2는 state space model을 semiseparable matrix로 보는 sequence transformation 관점을 보여준다.

3.4 Computing State Space Models through Structured Matrix Algorithms

Theorem 3.5가 중요한 이유는 SSM(및 다른 시퀀스 모델)의 효율적인 계산 문제를 구조화된 행렬 곱셈을 위한 효율적인 알고리즘으로 축소할 수 있게 해주기 때문이다. 우리는 간략한 개요를 제공하고, SSM과 다른 시퀀스 모델 간의 등가성을 Section 4와 5에서 보여준 후, 우리의 주요 새 알고리즘은 Section 6으로 미룬다.

이전에 정의된 바와 같이, semiseparable matrix(즉, rank-structured matrix)는 고전적인 유형의 구조화된 행렬이다: (i) 이들은 $O(\mathrm{~T}^2)$ 대신 $O(\mathrm{~T})$ 파라미터만 갖는 SSS form과 같은 압축된 표현을 가진다. (ii) 이들은 압축된 표현에서 직접 작동하는 빠른 알고리즘을 가진다.

더 나아가, 파라미터화 및 행렬 곱셈 비용은 semiseparable order에서 tight할 수 있다. Proposition 3.6 (Pernet, Signargout, and Villard (2023)). 크기 T의 N-SS matrix는 $O(\mathrm{NT})$ 파라미터로 표현될 수 있으며, $O(\mathrm{NT})$ 시간 및 공간 복잡도로 행렬-벡터 곱셈을 수행한다.

예를 들어, 1-SS matrix는 이러한 연결의 본질을 보여준다. $M=1 \mathrm{SS}(a)$ 행렬은 정확히 $\mathrm{T}-1$개의 파라미터 $a_{0: \mathrm{T}-1}=a_{1}, \ldots, a_{\mathrm{T}-1}$로 정의되며, 스칼라 점화식 (7)을 따르면 $O(\mathrm{~T})$ 시간 내에 계산될 수 있다.

3.4.1 The Linear (Recurrent) Mode

Proposition 3.6은 **대각선 구조의 SSM(S4D (Gu, Gupta, et al. 2022))**의 경우, state space model 공식 (2)를 활용하여 recurrence를 전개하는 것만으로 쉽게 확인할 수 있다. 우리는 공식적인 tensor-contraction 알고리즘을 (8)에 제시하며, 여기서 차원 $S$는 $T^4$와 같다.

$$\begin{aligned} Z & =\operatorname{contract}(\mathrm{SP}, \mathrm{SN} \rightarrow \mathrm{SPN})(X, B) \\ H & =\operatorname{contract}(\mathrm{TSN}, \mathrm{SPN} \rightarrow \mathrm{TPN})(L, Z) \\ Y & =\operatorname{contract}(\mathrm{TN}, \mathrm{TPN} \rightarrow \mathrm{TP})(C, H) \end{aligned}$$

여기서 $L \in \mathbb{R}^{(\mathrm{T}, \mathrm{T})}$은 $1 \mathrm{SS}(A)$로 정의되거나, 다른 말로 $i \in[\mathrm{~N}]$에 대해 $L_{0: \mathrm{T}, 0: \mathrm{T}}=1 \mathrm{SS}\left(A_{0: \mathrm{T}}\right)$로 정의된다. 이 알고리즘은 (2)에 해당하는 세 단계를 포함한다: (i) 입력 $X$를 입력 행렬 $B$로 확장 (8a), (ii) 독립적인 scalar SSM recurrence를 전개 (8b), (iii) hidden state $H$를 출력 행렬 $C$로 수축 (8c).

우리는 단계 (8b)에서 scalar SSM과 1-SS 행렬 간의 등가성을 사용했음에 유의한다. Remark 3. 우리는 (8)이 Mamba (S6) 모델의 특수한 경우임을 주목한다. 그러나 naive한 구현은 (T, P, N) 크기의 확장된 텐서 $Z$와 $H$ 때문에 느리다. Gu와 Dao (2023)는 이러한 텐서들을 실제로 생성하는 것을 피하기 위한 하드웨어-인지 구현을 도입했다.

놀랍게도, Theorem 3.5와 Proposition 3.6은 모든 SSM이 알고리즘 (8)과 동일한 점근적 효율성을 가진다는 것을 즉시 암시한다.

Theorem 3.7. 상태 크기 N, 시퀀스 길이 T를 가지는 모든 state space model (정의 2.2)은 $O(\mathrm{TN})$ 시간에 계산될 수 있다 (잠재적인 전처리 제외).

이 결과는 structured SSM 문헌에서 새로운 것임을 주목한다. 특히, dense하고 비구조적인 $A_t$ 행렬이 주어졌을 때, 총 표현(representation)만으로도 $O(\mathrm{TN}^2)$ 크기인 것으로 보인다. 따라서 Theorem 3.7은 전처리 단계를 통해 비구조적인 SSM조차도 최적으로 효율적으로 계산될 수 있으며, 상한이 $B$와 $C$의 크기로 주어지는 하한 $O(\mathrm{TN})$과 일치한다는 비자명한 결과를 제시한다.

Remark 4. Theorem 3.7은 $\mathbb{R}^{(\mathrm{N}, \mathrm{N})}$에 걸쳐 있는 거의 모든 dense 행렬이 $\mathbb{C}$에 걸쳐 대각화 가능하며, 이는 거의 모든 dense real SSM이 대각선 복소수 SSM과 동등하다는 결과로 이어진다는 사실을 고려할 때 그리 놀랍지 않을 수 있다. 이 사실은 대각선 SSM이 structured SSM의 가장 인기 있는 형태인 이유를 뒷받침한다 (Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; 7. T. Smith, Warrington, and Linderman 2023). 그러나 Theorem 3.7은 모든 real SSM(대각화 가능한 것뿐만 아니라)과 다른 필드(© 자체 포함)에 걸쳐 있는 dense SSM에 대해 훨씬 더 강력한 결과를 암시한다.

실제로, 효율적으로 계산 가능한 SSM은 여전히 $A$에 추가적인 구조를 요구하며, 특히 비용이 많이 드는 전처리 단계(N차 FLOPs와 특이값 분해와 같은 하드웨어 비효율적인 연산 포함)를 피하기 위해 필요하다. 이러한 구조는 structured SSM(예: S4(D) 및 Mamba)에 대한 과거 연구와 우리의 새로운 알고리즘의 초점이다. 특히, $A$에 약간 더 강력한 구조가 부과될 때, 우리는 Section 6에서 SSM 행렬 $M=\operatorname{SSS}(A, B, C)$의 블록 분해를 통해 매우 하드웨어 효율적인 알고리즘을 설계할 것이다.

3.4.2 The Quadratic (Naive) Mode

우리는 새로운 행렬 관점에서 드러나는 SSM을 계산하는 또 다른 방법이 있음을 주목한다. 행렬 SSM 표현 (3)을 naive하게 계산하는 것은 단순히 시퀀스 변환 행렬 $M=\operatorname{SSS}(A, B, C)$를 **구체화(materializing)**하는 것을 포함한다. 이는 $(T, T)$ 행렬이므로, 이 naive 알고리즘은 시퀀스 길이에 대해 이차적으로(quadratically) 확장될 것이다. 그러나 시퀀스 길이 $T$가 짧을 때는, 상수 요인과 계산 패턴의 하드웨어 친화성(예: 행렬-행렬 곱셈 활용) 덕분에 선형 알고리즘보다 실제로 더 효율적일 수 있다. 사실, 구조화된 SSM의 특정 경우에는 이는 quadratic attention 계산과 매우 유사하게 보인다 (Section 5).

3.4.3 Summary

많은 시퀀스 모델은 **행렬 시퀀스 변환(matrix sequence transformation)**으로 명시적으로 동기 부여되거나 정의된다. 가장 대표적인 예시는 Transformer이며, 여기서 행렬 믹서(matrix mixer)는 attention matrix이다. 반면, RNN과 SSM은 이전에는 이러한 방식으로 설명된 적이 없다.

우리는 state space model의 명시적인 행렬 변환 형태를 제공함으로써, 이를 이해하고 사용하는 새로운 방법을 제시한다. 계산적인 관점에서, state space model의 forward pass를 계산하는 모든 방법은 semiseparable matrix에 대한 행렬 곱셈 알고리즘으로 볼 수 있다. 이 semiseparable matrix 관점은 **state space duality (SSD)**를 이해하는 하나의 렌즈를 제공하며, 여기서 dual mode는 각각 선형 시간 semiseparable matrix 곱셈 알고리즘과 이차 시간 naive matrix 곱셈을 의미한다.

더 나아가, semiseparable matrix의 풍부한 구조를 활용하면 더 나은 알고리즘과 더 많은 통찰력을 얻을 수 있다 (예: Section 6 및 Appendix B). Appendix C.1에서는 semiseparable matrix의 몇 가지 추가적인 속성을 설명한다.

4 Structured Masked Attention: Generalizing Linear Attention with Structured Matrices

이 섹션에서는 선형 attention 프레임워크를 기본 원리부터 다시 살펴본다. 이 섹션의 주요 결과는 선형 attention에 대한 간단한 텐서-축약 기반 증명(Proposition 4.1)과 구조화된 masked attention에 대한 일반화된 추상화(Definition 4.2)이다. 이 섹션은 state space model과는 다른 방향에서 주요 duality 결과들을 도출하며, Section 3과 완전히 독립적으로 읽을 수 있음을 밝힌다.

• Section 4.1에서는 kernel attention 및 masked kernel attention에 특별히 초점을 맞춰 다양한 attention 변형에 대한 프레임워크를 설정한다.
• Section 4.2에서는 텐서 축약의 관점에서 선형 attention에 대한 간단한 증명을 제공하며, 이는 우리의 첫 번째 주요 attention 결과이다.
• Section 4.3에서는 구조화된 행렬을 통해 기존 attention 변형을 일반화한 structured masked attention을 정의한다.

4.1 The Attention Framework

4.1.1 Attention

단일 헤드(single-head) attention의 기본 형태는 세 개의 벡터 시퀀스 $(Q, K, V)$를 $Y$로 매핑하는 함수이다.

$$\begin{array}{rlr} Q & =\text { input } & (\mathrm{T}, \mathrm{~N}) \\ K & =\text { input } & (\mathrm{S}, \mathrm{N}) \\ V & =\text { input } & (\mathrm{S}, \mathrm{P}) \\ G & =Q K^{\top} & (\mathrm{T}, \mathrm{S}) \\ M & =f(G) & (\mathrm{T}, \mathrm{S}) \\ Y & =G V & (\mathrm{~T}, \mathrm{P}) \end{array}$$

우리는 텐서의 차원을 나타내기 위해 "$Q \in \mathbb{R}^{(\mathrm{T}, \mathrm{N})}$"와 같은 "shape annotation"을 사용한다. 이 일반적인 형태에서 S와 T는 각각 소스(source) 및 타겟(target) 시퀀스 길이를 나타내고, N은 feature 차원, P는 head 차원을 나타낸다.

가장 일반적인 softmax attention 변형은 softmax activation $f=$ softmax를 사용하여 $G$ 행렬의 행(row)을 정규화한다.

4.1.2 Self-Attention

우리의 접근 방식은 self-attention의 가장 중요한 경우에서 영감을 받았다. 이 경우: (i) source 시퀀스와 target 시퀀스가 동일하고 (즉, $\mathrm{S}=\mathrm{T}$ ), (ii) 일반적으로 feature dimension과 head dimension이 동일하며 (즉, $\mathrm{N}=\mathrm{P}$ ), (iii) $Q, K, V$는 동일한 입력 벡터에 대한 선형 투영(linear projection)을 통해 생성된다 ($Q=W_{Q} \cdot X, K=W_{K} \cdot X, V=W_{V} \cdot X$).

그러나 본 논문에서는 이러한 세부 사항들을 추상화하고, $Q, K, V$ 행렬로부터 논의를 시작한다.

Remark 5. 우리의 초점은 head dimension과 feature dimension이 동일한 self-attention 경우에 맞춰져 있으며 (즉, $\mathrm{S}=\mathrm{T}$ 및 $\mathrm{N}=\mathrm{P}$), 이를 주요 예시로 사용할 것이다. 우리가 attention의 일반적인 공식을 정의하는 이유는, 우리 프레임워크가 cross-attention과 같은 변형들을 포괄할 수 있도록 하기 위함뿐만 아니라, 차원 표기법(예: S와 T)을 분리함으로써 이 섹션의 주요 결과에 대한 contraction notation 증명을 더욱 명확하게 만들기 위함이다.

Remark 6. Attention은 일반적으로 세 개의 입력 $Q, K, V$에 대한 연산으로 대칭적으로 다루어지지만, Equation (9)의 입력 및 출력 차원은 그렇지 않음을 나타낸다. 특히, feature dimension N은 출력에 존재하지 않는다. 따라서 $\mathrm{S}=\mathrm{T}$인 경우(예: self-attention)에는 $V$를 주된 입력으로 간주하여, Equation (9)가 적절한 시퀀스 변환 $V \mapsto Y$를 정의하도록 한다 (Definition 2.1).

4.1.3 Kernel Attention

Gram 행렬 $G$에 softmax 함수를 적용하는 단계는 두 부분으로 분해될 수 있다:

1. $G$ 행렬을 **지수화(exponentiating)**하는 단계.
2. $S$ 축을 따라 $G$ 행렬을 **정규화(normalizing)**하는 단계.

정규화 항은 $V=1$을 전달하고 나누는 것과 같으므로 지금은 무시할 수 있다 (이에 대해서는 Section 7.3에서 다시 다룬다). 지수화 항은 kernel 변환으로 볼 수 있다: $\exp(QK^\top) = \varphi(Q)\varphi(K)^\top$와 같은 (무한 차원) feature map $\varphi$가 존재한다. feature map을 $Q$와 $K$ 자체의 정의(즉, $Q, K$를 변환 후 버전으로 정의)로 추상화함으로써, 우리는 softmax 변환을 무시하고, $Q, K$가 kernel feature map에 의해 임의로 생성되며 잠재적으로 $N \neq P$라고 가정할 수 있다.

Kernel attention의 많은 인스턴스들이 제안되었으며, 다음을 포함한다:

• 원래의 Linear Attention (Katharopoulos et al. 2020)은 kernel feature map을 $x \mapsto 1+\operatorname{elu}(x)$와 같은 임의의 pointwise activation function으로 정의한다.
• Random Feature Attention (RFA) (H. Peng et al. 2021)은 Gaussian kernel의 random Fourier feature approximation (Rahimi and Recht 2007)을 사용하여 softmax attention (즉, exp feature map)을 근사화하도록 kernel feature map을 선택한다. 이는 random projection (즉, $Q$와 $K$에 random projection $W$를 곱하고 활성화 함수 $x \mapsto (\cos(x), \sin(x))$를 적용)을 포함한다.
• Performer (Choromanski et al. 2021)는 positive orthogonal random features (FAVOR+)를 통한 빠른 attention을 제안한다. positive random features (PRF) 부분은 kernel feature map을 random projection에 이어 feature map $x \mapsto 2^{-1/2}(\exp(x), \exp(-x))$로 선택한다. 이 선택은 kernel 요소들이 양수 값을 가지며 softmax attention을 증명 가능하게 근사화하도록 동기 부여된다. [또한 orthogonal 방향으로 random projection을 선택하는 것을 제안하지만, 우리는 고려하지 않는다.]
• cosFormer (Qin, Weixuan Sun, et al. 2022)는 RFA에 cosine reweighting mechanism을 추가하여 위치 정보(positional information)를 통합하여 지역성(locality)을 강조한다. 이는 효과적으로 $Q_t, K_t$를 feature map $x \mapsto (x \cos(\pi t / 2 T), \sin(\pi t / 2 T))$를 통해 전달한다.
• Linear Randomized Attention (Zheng, C. Wang, and Kong 2022)은 importance sampling 관점에서 RFA를 일반화하고, 전체 softmax kernel (단순히 exp-변환된 분자가 아닌)에 대한 더 나은 추정치를 제공하도록 일반화한다.

다른 관련 attention 변형으로는 Linformer (Sinong Wang et al. 2020)와 Nyströformer (Xiong et al. 2021)가 있으며, 이 둘은 모두 attention 행렬 $M$의 **저랭크 근사(low-rank approximation)**를 사용한다 (따라서 방정식 (9)와 호환된다). 각각 random projection (Johnson-Lindenstrauss)과 kernel approximation (Nyström method)을 통해 이를 수행한다.

4.1.4 Masked (Kernel) Attention

$L$을 (T, S) 형태의 mask라고 하자. 가장 일반적으로, autoregressive self-attention의 경우 S=T일 때, $L$은 causal mask를 나타내는 1로 구성된 하삼각 행렬(lower-triangular matrix)일 수 있다. causality를 강제하는 것 외에도, banded, dilated, block diagonal과 같은 다양한 sparsity pattern을 적용할 수 있으며, 이는 dense attention의 복잡도를 줄이는 데 목적이 있다.

Masked attention은 일반적으로 행렬 표기법으로 다음과 같이 표현된다:

$$y=\left(L \circ\left(Q K^{\top}\right)\right) \cdot V$$

더 정확하게는, 형태(shape) 주석과 함께 계산 순서를 세분화하면 다음과 같다:

$$\begin{aligned} G & =Q K^{\top} & (\mathrm{T}, \mathrm{~S}) \\ M & =G \circ L & (\mathrm{~T}, \mathrm{~S}) \\ Y & =M V & (\mathrm{~T}, \mathrm{P}) \end{aligned}$$

이 섹션에서 제시하는 attention variant에 대한 개선된 유도는 이 공식이 단일 contraction으로 작성될 수 있다는 점을 주목하는 것에서 시작한다:

$$Y=\operatorname{contract}(\mathrm{TN}, \mathrm{SN}, \mathrm{SP}, \mathrm{TS} \rightarrow \mathrm{TP})(Q, K, V, L)$$

그리고 (11)의 알고리즘은 특정 순서의 pairwise contraction을 통해 (12)를 계산하는 것으로 재구성될 수 있다:

$$\begin{aligned} G & =\operatorname{contract}(\mathrm{TN}, \mathrm{SN} \rightarrow \mathrm{TS})(Q, K) \\ M & =\operatorname{contract}(\mathrm{TS}, \mathrm{TS} \rightarrow \mathrm{TS})(G, L) \\ Y & =\operatorname{contract}(\mathrm{TS}, \mathrm{SP} \rightarrow \mathrm{TP})(M, V) \end{aligned}$$

4.2 Linear Attention

Linear attention과 다른 많은 효율적인 attention 변형들은 종종 핵심 attention 계산인 $\left(Q K^{\top}\right) V=Q\left(K^{\top} V\right)$에서 행렬 결합 순서(matrix associativity)를 변경하는 방식으로 동기 부여된다. 그러나 mask가 추가될 경우, 이러한 유도는 다소 덜 직관적이다 (예를 들어, 원본 논문 (Katharopoulos et al. 2020) 및 변형 연구 (Y. Sun et al. 2023)에서는 증명 없이 공식을 제시한다).

대략적으로, linear attention 방법은 다음 공식이 (10)과 동등하다고 주장하며, 이는 합을 전개하고 인덱스를 신중하게 추적하여 검증해야 한다.

$$Y=Q \cdot \text { cumsum }\left(K^{\top} V\right)$$

Proposition 4.1 ((Katharopoulos et al. 2020)): Autoregressive kernel attention, 즉 causal mask가 적용된 masked kernel attention은 단계별로 상수 시간(constant time)이 소요되는 recurrence 관계를 통해 $O(T)$ 시간에 계산될 수 있다.

4.2.1 A Tensor Contraction Proof of Linear Attention

우리는 linear attention에 대한 간단하고 엄밀한 유도 과정을 제시하며, 이를 통해 일반화 방법도 즉시 드러날 것이다. 핵심 아이디어는 수축(contraction) (12)를 다른 순서로 수행하는 것이다. 우리는 모호한 행렬 표기법을 피하고 수축 표기법(contraction notation)을 직접 사용한다:

$$\begin{aligned} Z & =\operatorname{contract}(\mathrm{SP}, \mathrm{SN} \rightarrow \mathrm{SPN})(V, K) \\ H & =\operatorname{contract}(\mathrm{TS}, \mathrm{SPN} \rightarrow \mathrm{TPN})(L, Z) \\ Y & =\operatorname{contract}(\mathrm{TN}, \mathrm{TPN} \rightarrow \mathrm{TP})(Q, H) \end{aligned} \quad(\mathrm{T}, \mathrm{P}, \mathrm{~N})$$

직관적으로, 우리는 이 수축 순서를 다음과 같이 해석한다. 첫 번째 단계 (15a)는 **feature 차원 N의 인자만큼 더 많은 feature로 "확장(expansion)"**을 수행한다. 세 번째 단계 (15c)는 확장된 feature 차원을 다시 수축시킨다. 만약 $K$를 입력으로 본다면 (Remark 6), $V$와 $Q$는 각각 확장과 수축을 수행한다.

두 번째 단계가 가장 중요하며, linear attention의 "linear" 부분을 설명한다. 먼저 (15b)가 단순히 $L$에 의한 직접적인 행렬 곱셈이라는 점에 주목하라 ((P, N) 축을 평탄화할 수 있기 때문). 또한, 이 항만이 T와 S 축을 모두 포함하며, 따라서 $\Omega(\mathrm{TS})$ 복잡도(즉, 시퀀스 길이에 대해 이차)를 가져야 한다는 점에 주목하라. 그러나 마스크 $L$이 **표준적인 causal attention mask(하삼각 행렬의 모든 원소가 1)**일 때, $L$에 의한 행렬-벡터 곱셈은 feature-wise cumulative sum과 동일하다.

$$y=\left[\begin{array}{ccc} 1 & & \\ \vdots & \ddots & \\ 1 & \ldots & 1 \end{array}\right] x \quad \Longleftrightarrow \quad \begin{aligned} & y_{0}=x_{0} \\ & y_{t}=y_{t-1}+x_{t} \end{aligned}$$

4.3 Structured Masked Attention

masked attention (15)의 텐서 축약(tensor contraction) 관점에서 볼 때, 우리는 원래 linear attention의 핵심이 인과 마스크(causal mask)에 의한 행렬-벡터 곱셈이 누적 합(cumulative sum) 연산자와 동일하다는 사실임을 즉시 알 수 있다.

그러나 우리는 attention mask가 반드시 모두 1일 필요는 없다는 것을 관찰했다. linear attention이 빠르게 동작하기 위해 필요한 것은 $L$이 구조화된 행렬(structured matrix)이어야 한다는 것뿐이며, 정의상 구조화된 행렬은 빠른 행렬 곱셈을 가진 행렬을 의미한다 (Section 2.3). 특히, 우리는 sub-quadratic (이상적으로는 linear) 행렬-벡터 곱셈을 가진 어떤 마스크 행렬 $L$이든 사용할 수 있으며, 이는 병목 방정식 (15b)의 속도를 높여 표준 linear attention과 동일한 복잡도를 가질 것이다.

정의 4.2. 구조화된 마스크드 어텐션(Structured masked attention, SMA) (또는 줄여서 구조화된 어텐션(structured attention))은 쿼리/키/값 $Q, K, V$와 **임의의 구조화된 행렬 $L$ (즉, sub-quadratic 행렬 곱셈을 가짐)**에 대한 함수로 정의되며, 4-way 텐서 축약을 통해 표현된다:

$$Y=\operatorname{contract}(\mathrm{TN}, \mathrm{SN}, \mathrm{SP}, \mathrm{TS} \rightarrow \mathrm{TP})(Q, K, V, L) .$$

SMA의 quadratic mode 알고리즘은 (13)에 의해 정의된 쌍별 축약(pairwise contractions)의 시퀀스이며, 이는 표준 (masked) attention 계산에 해당한다.

SMA의 linear mode 알고리즘은 (15)에 의해 정의된 쌍별 축약의 시퀀스이며, 여기서 단계 (15b)는 subquadratic 구조화된 행렬 곱셈을 통해 최적화된다.

우리는 구조화된 마스크드 어텐션을 주어진 행렬 구조의 어떤 클래스에도 인스턴스화할 수 있다. 몇 가지 예시는 다음과 같다 (Figure 3):

• Linear attention은 **인과 마스크(causal mask)**를 사용한다.
• **RetNet (Y. Sun et al. 2023)**은 특정 감쇠 계수 $\gamma \in[0,1]$에 대해 **감쇠 마스크(decay mask) $L_{i j}=\gamma^{i-j} \cdot \mathbb{I}[j \geq i]$**를 사용한다.

Figure 3: (Structured Masked Attention.) SMA는 임의의 구조화된 행렬 $L$에 대해 마스크드 어텐션 행렬 $M=Q K^{\top} \circ L$을 구성하며, 이는 행렬 시퀀스 변환 $Y=M V$를 정의한다. 모든 SMA 인스턴스는 다른 축약 순서와 $L$에 의한 효율적인 구조화된 행렬 곱셈을 결합하여 유도되는 이중 subquadratic 형태를 가진다. 이전 예시로는 **Linear Attention (Katharopoulos et al. 2020)**과 **RetNet (Y. Sun et al. 2023)**이 있다. 본 논문의 초점인 SSD (1-semiseparable SMA) 외에도, 구조화된 어텐션의 다른 많은 잠재적 인스턴스화가 가능하다.

• 감쇠 마스크는 학습 가능한 (또는 입력 의존적인) 파라미터 집합 $\alpha \in \mathbb{R}^{\top}$에 대해 Toeplitz 행렬 $L_{i j}=\alpha_{i-j}$로 일반화될 수 있다. 이는 AliBi (Press, N. Smith, and Lewis 2022)와 같은 다른 방법들을 연상시키는 일종의 상대적 위치 인코딩으로 해석될 수 있지만, 덧셈이 아닌 곱셈 방식이다.
• 또 다른 변형은 Fourier 행렬 $L_{i j}=\omega^{i j / \top}$을 사용하여 위치 구조를 다른 방식으로 인코딩할 수 있다.

Section 5에서는 semiseparable SMA를 다루며, 이는 우리의 주요 SSD 모델을 정의한다.

4.3.1 Summary: The Dual Forms of Masked Attention

Standard (masked kernel) attention은 종종 함수와 알고리즘 사이에서 혼동된다. 이러한 구분을 명확히 하면 다양한 attention 변형들을 이해하는 데 도움이 된다.

• 우리는 masked attention을 특정 함수 (12)로 간주한다.
• 표준적인 quadratic attention 계산 (13)은 이 함수를 계산하는 하나의 알고리즘으로 볼 수 있다.
• Linear attention (15)은 동일한 함수를 계산하는 또 다른 알고리즘이다.

더 나아가, 이 경우

• masked attention 함수는 단순히 네 개의 항에 대한 특정 contraction이다.
• quadratic attention과 linear attention 알고리즘은 단순히 contraction을 수행하는 두 가지 다른 순서이다.

Contraction 순서는 계산 복잡도에 큰 차이를 만들 수 있으며, 이는 quadratic과 linear 분할로 이어진다. State space model이 여러 방식으로 계산될 수 있는 변환이며, dual quadratic과 linear 형태를 가지는 것과 마찬가지로 (Section 3.4), linear attention도 두 가지 contraction 순서에서 비롯되는 유사한 duality를 가진다. 사실, 이들은 동일한 근본적인 duality에 대한 다른 관점임이 밝혀지며, 이는 Section 5에서 명확히 설명한다.

5 State Space Duality

Section 3과 4에서는 structured state space model과 structured attention을 정의하고, 그 특성을 논의하며, 두 가지 모두 quadratic 알고리즘과 linear 알고리즘을 가짐을 보였다. 이 섹션에서는 이 둘을 연결한다. 우리의 주요 결과는 structured state space model의 특정 경우가 structured attention의 특정 경우와 일치하며, linear-time SSM 알고리즘과 quadratic-time kernel attention 알고리즘이 서로의 dual form임을 보여주는 것이다.

• Section 5.1에서는 state space model을 scalar structure로 특수화하여, naive quadratic 계산이 kernel attention의 한 예시로 볼 수 있음을 설명한다.
• Section 5.2에서는 structured masked attention을 semiseparable SMA로 특수화하며, 이는 효율적인 autoregression을 갖는 masked attention을 특징짓는다.
• Section 5.3에서는 structured masked attention과 structured state space model 간의 연결을 structured state space duality라고 명명하여 요약한다.

5.1 Scalar-Identity Structured State Space Models

Section 3에서 우리는 **state space model (SSM)**이 semiseparable matrix 변환과 동등하며, 이는 선형 recurrent 형태와 이차 naive 형태를 모두 가진다는 것을 보였다.

SSM은 $y=\operatorname{SSM}(A, B, C)(x)$로 정의되며, SSM의 행렬 형태는 SSS (sequentially semiseparable) 표현 $M=\operatorname{SSS}(A, B, C)$를 사용한다. 여기서 $M_{j i}=C_{j}^{\top} A_{j: i} B_{i}$ (식 (3))이다. 이제 $A_{j}$가 단순히 스칼라인 경우를 고려해보자. 즉, $A$ 행렬이 극도로 구조화된 structured SSM의 한 인스턴스인 경우, $A=a I$ (스칼라 $a$와 항등 행렬 $I$)이다. 그러면 다음과 같이 재배열할 수 있다.

$$M_{j i}=A_{j: i} \cdot\left(C_{j}^{\top} B_{i}\right) .$$

그리고 이는 다음과 같이 벡터화될 수 있다.

$$\begin{aligned} L & :=1 \operatorname{SS}(a) \\ M & =L \circ\left(C B^{\top}\right) \end{aligned}$$

여기서 $B, C \in \mathbb{R}^{(\mathrm{T}, \mathrm{N})}$이다. 이 공식을 사용하면, 전체 출력 $Y=M X$는 다음과 같이 정확하게 계산된다.

$$\begin{aligned} G & =\operatorname{contract}(\mathrm{TN}, \mathrm{SN} \rightarrow \mathrm{TS})(C, B) \\ M & =\operatorname{contract}(\mathrm{TS}, \mathrm{TS} \rightarrow \mathrm{TS})(G, L) \\ Y & =\operatorname{contract}(\mathrm{TS}, \mathrm{SP} \rightarrow \mathrm{TP})(M, X) \end{aligned}$$

여기서 $S=T$이다. 그런데 이는 masked kernel attention 정의 (13)와 정확히 동일하다! 따라서 Section 3.4에서 언급했듯이, 스칼라 structured SSM을 naive하게 계산하는 것 (즉, semiseparable matrix $M$을 구체화하고 이차 행렬-벡터 곱셈을 수행하는 것)은 이차 masked kernel attention과 정확히 동일하다.

5.2 1-Semiseparable Structured Masked Attention

Structured masked attention은 모든 structured mask $L$의 사용을 허용한다. $L$이 causal mask일 때, 이는 표준적인 linear attention이 된다. causal mask는 $L=\operatorname{SS}\left(1_{T}\right)$이며, 즉 정의 (6)에서 $a_{t}=1$일 때 1-SS mask가 생성된다. 이는 $L$을 1-semiseparable mask 클래스, 또는 **1-semiseparable structured masked attention (1-SS SMA)**으로 일반화하는 동기가 된다. 여기서 linear attention의 recurrence에 있는 cumsum은 더 일반적인 recurrence인 scalar SSM scan, 즉 1-semiseparable matrix multiplication으로 대체된다 (Section 3.2.2).

마지막으로, 우리가 1-semiseparable SMA를 고려하는 가장 중요한 이유는 이를 계산하는 **선형 형태(linear form)**가 diagonal state space model의 특수한 경우이기 때문이다. SMA의 선형 형태는 알고리즘 (15)이며, 여기서 병목 단계 (15b)는 1-SS mask에 의한 행렬 곱셈으로 볼 수 있다. Section 3에서는 diagonal SSM (8)의 계산도 설명했는데, 여기서 병목 단계 (8b)는 scalar SSM recurrence이며 이는 1-SS 곱셈과 동일하다. 유일한 차이점은 (8b)가 $L$에 추가적인 N 차원을 가진다는 것이다. 이는 행렬 $A$가 크기 N의 diagonal matrix이기 때문이다. 만약 $A$의 모든 대각선 항목이 동일하다면 이 N 차원은 사라지며, 이는 Corollary 5.1로 이어진다.

Corollary 5.1. 1-SS SMA (1-semiseparable structured matrix $L$을 사용한 masked attention) (15)는 diagonal matrix가 항등 행렬의 스칼라 배수인 diagonal SSM (8)의 특수한 경우이다.

Corollary 5.1은 1-SS SMA가 효율적인 recurrent form을 가진다고 말하지만, 우리는 또한 SMA의 어떤 인스턴스가 효율적인 autoregression을 가지는지를 특징짓는 역 결과도 보여줄 수 있다.

Theorem 5.2. 유한한 차수(bounded order)를 가진 autoregressive process인 structured masked attention (정의 4.2)의 모든 인스턴스에 대해, structured mask $L$은 semiseparable matrix여야 한다.

다시 말해, 효율적인 autoregressive attention은 일반적인 semiseparable SMA이다. Theorem 5.2는 Appendix C.2에서 증명된다. Remark 7. 1-semiseparable SMA는 state space model의 특수한 경우이지만, 일반적인 semiseparable SMA는 1-SS SMA보다 엄격하게 더 표현력이 풍부하며, 표준 SSM으로는 설명될 수 없다. 그러나 $L$에 의한 semiseparable 곱셈과 SMA의 선형 형태 (식 (15a))는 각각 확장 및 수축 단계를 포함하며, 단일 (더 큰) 확장을 가진 유사한 1-SS SMA 인스턴스에 흡수될 수 있다.

요약하자면, 1-semiseparable structured attention은 SMA의 가장 중요한 경우이다. 그 이유는 다음과 같다:

• 입력 의존적인 recurrence를 가진 linear attention의 자연스러운 일반화이다.
• 효율적인 autoregressive attention과 동일한 일반적인 semiseparable attention의 가장 간단한 경우이다.
• diagonal state space model의 특수한 경우이다.

5.3 Structured State-Space Duality (SSD)

우리의 결과를 요약하면 다음과 같다:

• Structured state-space model (SSM) (Section 3)은 일반적으로 선형 시간(linear-time) 재귀(recurrence)로 정의되는 모델이다. 그러나 선형 sequence-to-sequence 변환을 특징짓는 행렬 공식을 확장함으로써, 이차 형식(quadratic form)을 도출할 수 있다.
• Attention variants (Section 4)는 이차 시간(quadratic-time) 쌍별 상호작용(pairwise interaction)을 통해 정의되는 모델이다. 그러나 이를 4방향 텐서 축약(four-way tensor contraction)으로 보고 다른 순서로 축약함으로써, 선형 형식(linear form)을 도출할 수 있다.
• 각각의 자연스러운 특수 사례, 즉 $A$ 행렬에 스칼라-항등(scalar-identity) 구조를 가진 state space model과 $L$ 마스크에 1-semiseparable 구조를 가진 structured masked attention은 **정확히 동일한 선형 및 이차 형식을 가진 서로의 이중(dual)**이다.

Figure 4는 이 두 표현 간의 이중성을 요약한다. 확장된 관련 연구 및 논의 (Section 10)에서는 SSD와 일반 SSMs/attention 간의 관계를 더 자세히 설명한다.

6 A Hardware-Efficient Algorithm for SSD Models

SSM, attention, 그리고 structured matrix 간의 이론적인 SSD 프레임워크를 개발하는 이점은 이러한 연결을 활용하여 모델과 알고리즘을 개선하는 데 있다. 이 섹션에서는 structured matrix multiplication을 계산하는 다양한 알고리즘으로부터 SSD 모델을 효율적으로 계산하는 여러 알고리즘을 어떻게 도출할 수 있는지 보여준다.

우리의 주요 계산 결과는 선형(recurrent) 모드와 2차(attention) 모드를 모두 결합한 SSD 모델 계산 알고리즘이다. 이 알고리즘은 **SSM만큼 계산 효율적(시퀀스 길이에 대해 선형 스케일링)**이며, **attention만큼 하드웨어 친화적(주로 행렬 곱셈 사용)**이다.

Theorem 6.1. 상태 확장 계수 N과 헤드 차원 $\mathrm{P}=\mathrm{N}$을 갖는 SSD 모델을 고려한다. 임의의 입력 $X \in \mathbb{R}^{(\mathrm{T}, \mathrm{P})}$에 대해 모델을 계산하는 알고리즘이 존재하며, 이 알고리즘은 $O\left(\mathrm{TN}^{2}\right)$의 학습 FLOPs, $O(\mathrm{TN})$의 추론 FLOPs, $O\left(\mathrm{~N}^{2}\right)$의 추론 메모리만을 요구하며, 작업은 행렬 곱셈에 의해 지배된다.

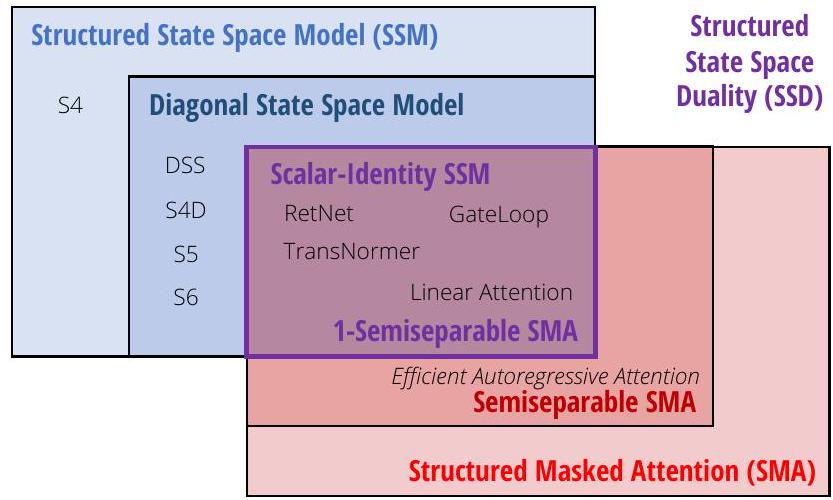
Figure 4: (Structured State Space Duality.) State space duality는 state space model과 masked attention 간의 밀접한 관계를 설명한다. 왼쪽: 일반적인 SSM과 SMA는 모두 선형 및 2차 형태를 가지며, 표기법에서 직접적인 유사성을 보인다. 오른쪽: SSM과 SMA는 많은 시퀀스 모델을 특수한 경우로 포괄하는 광범위한 state space dual model (SSD) 클래스에서 교차한다.

이러한 모든 경계는 tight하다. 왜냐하면 헤드 크기 N에서 작동하는 상태 확장 N을 가진 state space model은 **총 상태 크기가 $\mathrm{N}^{2}$**이므로 (학습 및 추론 FLOPs의 하한이 각각 $O\left(\mathrm{TN}^{2}\right)$ 및 $O\left(\mathrm{~N}^{2}\right)$이 됨), 입력 $X$ 자체는 TN 요소를 가지므로 메모리 하한을 제공한다.

Theorem 6.1의 주요 아이디어는 state space model을 계산하는 문제를 semiseparable matrix multiplication으로 다시 보는 것이지만, 그 구조를 새로운 방식으로 활용하는 것이다. recurrent 또는 attention 모드에서 전체 행렬을 계산하는 대신, 행렬의 블록 분해(block decomposition)를 수행한다. 대각선 블록은 dual attention 모드를 사용하여 효율적으로 행렬 곱셈으로 계산할 수 있으며, 비대각선 블록은 semiseparable matrix의 rank-structure에 의해 인수분해되어 더 작은 recurrence로 축소될 수 있다. Listing 1은 SSD 알고리즘의 자체 포함된 구현을 제공한다. Gu and Dao (2023)의 일반적인 selective SSM과 비교할 때, 이 구현은 훨씬 간단하며, 특수 저수준 커널 없이도 네이티브 PyTorch에서 상대적으로 효율적이다.

시작하기 위해, 우리는 행렬 $M$을 블록 크기 $Q$에 대해 $Q \times Q$ 크기의 부분 행렬로 구성된 $\frac{T}{Q} \times \frac{T}{Q}$ 그리드로 분할한다. 비대각선 블록은 semiseparable matrix의 정의 속성(Definition 3.1)에 의해 low-rank이다.

$$\begin{aligned} \text { (Block Decomposition) } \quad M & =\left[\begin{array}{cccc} M^{(0,0)} & & & \\ M^{(1,0)} & M^{(1,1)} & & \\ \vdots & \vdots & \ddots & \\ M^{(\top / Q-1,0)} & M^{(\top / Q-1,1)} & \ldots & M^{(\top / Q-1, \mathrm{~T} / Q-1)} \end{array}\right] \\ (\text { Diagonal Block }) & M^{(j, j)} \end{aligned}=\operatorname{SSM}\left(A_{j Q:(j+1) Q}, B_{j Q:(j+1) Q}, C_{j Q:(j+1) Q}\right) \quad A_{j Q-1:(i+1) Q-1}\left[\begin{array}{c} B_{i Q}^{\top} A_{(i+1) Q-1: i Q} \\ \vdots \\ B_{(i+1) Q-1}^{\top} A_{(i+1) Q-1:(i+1) Q-1} \end{array}\right]^{\top}$$

이는 예를 들어 $T=9$이고 $Q=3$ 길이의 청크로 분해하는 경우와 같이 예시를 통해 가장 쉽게 설명할 수 있다. 음영 처리된 셀은 semiseparable matrix의 비대각선 블록의 low-rank 인수분해이다.

\begin{aligned} & M=\left[\begin{array}{llllll} C_{0}^{\top} A_{0: 0} B_{0} & & & & & \\ C_{1}^{\top} A_{1: 0} B_{0} & C_{1}^{\top} A_{1: 1} B_{1} & & & & \\ C_{2}^{\top} A_{2: 0} B_{0} & C_{2}^{\top} A_{2: 1} B_{1} & C_{2}^{\top} A_{2: 2} B_{2} & & & \\ \hline C_{3}^{\top} A_{3: 0} B_{0} & C_{3}^{\top} A_{3: 1} B_{1} & C_{3}^{\top} A_{3: 2} B_{2} & C_{3}^{\top} A_{3: 3} B_{3} & & \\ C_{4}^{\top} A_{4: 0} B_{0} & C_{4}^{\top} A_{4: 1} B_{1} & C_{4}^{\top} A_{4: 2} B_{2} & C_{4}^{\top} A_{4: 3} B_{3} & C_{4}^{\top} A_{4: 4} B_{4} & \\ C_{5}^{\top} A_{5: 0} B_{0} & C_{5}^{\top} A_{5: 1} B_{1} & C_{5}^{\top} A_{5: 2} B_{2} & C_{5}^{\top} A_{5: 3} B_{3} & C_{5}^{\top} A_{5: 4} B_{4} & C_{5}^{\top} A_{5: 5} B_{5} \end{array}\right. \\ &\left.\hline \begin{array}{llllll} C_{6}^{\top} A_{6: 0} B_{0} & C_{6}^{\top} A_{6: 1} B_{1} & C_{6}^{\top} A_{6: 2} B_{2} & C_{6}^{\top} A_{6: 3} B_{3} & C_{6}^{\top} A_{6: 4} B_{4} & C_{6}^{\top} A_{6: 5} B_{5} \\ C_{7}^{\top} A_{7: 0} B_{0} & C_{7}^{\top} A_{7: 1} B_{1} & C_{7}^{\top} A_{7: 2} B_{2} & C_{6}^{\top} A_{6: 6} B_{6} & \\ C_{8}^{\top} A_{8: 0} B_{0} & C_{8}^{\top} A_{8: 1} B_{1} & C_{8}^{\top} A_{8: 2} B_{2} & C_{7}^{\top} A_{7: 4} B_{4} & C_{7}^{\top} A_{7: 5} B_{5} & C_{7}^{\top} A_{7: 6} B_{6} \\ C_{7}^{\top} A_{7: 7} B_{7} & C_{8}^{\top} A_{8: 4} B_{4} & C_{8}^{\top} A_{8: 5} B_{5} & C_{8}^{\top} A_{8: 6} B_{6} & C_{8}^{\top} A_{8: 7} B_{7} & C_{8}^{\top} A_{8: 8} B_{8} \end{array}\right] \\ &=\left[\begin{array}{lllll} C_{0}^{\top} A_{0: 0} B_{0} & & & & \\ C_{1}^{\top} A_{1: 0} B_{0} & C_{1}^{\top} A_{1: 1} B_{1} & & & \\ C_{2}^{\top} A_{2: 0} B_{0} & C_{2}^{\top} A_{2: 1} B_{1} & C_{2}^{\top} A_{2: 2} B_{2} & & \\ \hline\left[\begin{array}{l} C_{3}^{\top} A_{3: 2} \\ C_{4}^{\top} A_{4: 2} \\ C_{5}^{\top} A_{5: 2} \end{array}\right] A_{2: 2}\left[\begin{l} B_{0}^{\top} A_{2: 0} \\ B_{1}^{\top} A_{2: 1} \\ B_{2}^{\top} A_{2: 2} \end{array}\right]^{\top} & C_{3}^{\top} A_{3: 3} B_{3} & \\ C_{4}^{\top} A_{4: 3} B_{3} & C_{4}^{\top} A_{4: 4} B_{4} & \\ C_{5}^{\top} A_{5: 3} B_{3} & C_{5}^{\top} A_{5: 4} B_{4} & C_{5}^{\top} A_{5: 5} B_{5} \end{array}\right] \\ & \hline\left[\begin{array}{l} C_{6}^{\top} A_{6: 5} \\ C_{7}^{\top} A_{7: 5} \\ C_{8}^{\top} A_{8: 5} \end{array}\right] A_{5: 2}\left[\begin{array}{l} B_{0}^{\top} A_{2: 0} \\ B_{1}^{\top} A_{2: 1} \\ B_{2}^{\top} A_{2: 2} \end{array}\right]^{\top} {\left[\begin{array}{l} C_{6}^{\top} A_{6: 5} \\ C_{7}^{\top} A_{7: 5} \\ C_{8}^{\top} A_{8: 5} \end{array}\right] A_{5: 5}\left[\begin{l} B_{3}^{\top} A_{5: 3} \\ B_{4}^{\top} A_{5: 4} \\ B_{5}^{\top} A_{5: 5} \end{array}\right]^{\top} } \\ &\left.\begin{array}{lll} C_{6}^{\top} A_{6: 6} B_{6} & & \\ C_{7}^{\top} A_{7: 6} B_{6} & C_{7}^{\top} A_{7: 7} B_{7} \\ C_{8}^{\top} A_{8: 6} B_{6} & C_{8}^{\top} A_{8: 7} B_{7} & C_{8}^{\top} A_{8: 8} B_{8} \end{array}\right] \end{aligned}

여기서부터 우리는 문제를 이 두 부분으로 줄일 수 있다. 이들은 또한 "청크" $y_{j Q:(j+1) Q}$의 출력을 두 가지 구성 요소로 나누는 것으로 해석될 수 있다: 청크 내 입력 $x_{j Q:(j+1) Q}$의 효과와 청크 이전 입력 $x_{0: j Q}$의 효과이다.

6.1 Diagonal Blocks

대각 블록은 단순히 더 작은 크기의 자기 유사 문제이므로 다루기 쉽다. $j$번째 블록은 범위 $R=j \mathrm{Q}:(j+1) \mathrm{Q}=(j \mathrm{Q}, j \mathrm{Q}+1, \ldots, j \mathrm{Q}+\mathrm{Q}-1)$에 대해 $\operatorname{SSM}\left(A_{R}, B_{R}, C_{R}\right)\left(x_{R}\right)$의 답을 계산하는 것을 나타낸다. 핵심은 이 블록이 원하는 어떤 방법으로든 계산될 수 있다는 것이다. 특히, 작은 chunk 길이 Q에 대해서는 dual quadratic SMA form을 사용하여 이 문제가 더 효율적으로 계산된다. 또한, 이 chunk들은 병렬로 계산될 수 있다.

이러한 하위 문제들은 초기 상태(chunk에 대한)가 0이라고 가정할 때 chunk당 출력은 무엇인가로 해석될 수 있다. 즉, chunk $j$에 대해 이는 chunk 입력 $x_{j Q}:(j+1) \mathrm{Q}$만을 고려하여 올바른 출력을 계산한다.

6.2 Low-Rank Blocks

low-rank factorization은 3개의 항으로 구성되며, 이에 상응하는 3개의 계산 부분이 있다. 이 factorization에서 우리는 다음 용어를 사용한다:

• $\left[\begin{array}{l}B_{0}^{\top} A_{2: 0} \\ B_{1}^{\top} A_{2: 1} \\ B_{2}^{\top} A_{2: 2}\end{array}\right]^{\top}$와 같은 항들은 right factor 또는 B-block-factor라고 불린다.
• $A_{5: 2}$와 같은 항들은 center factor 또는 A-block-factor라고 불린다.
• $\left[\begin{array}{l}C_{6}^{\top} A_{6: 5} \\ C_{7}^{\top} A_{7: 5} \\ C_{8}^{\top} A_{8: 5}\end{array}\right]$와 같은 항들은 left factor 또는 C-block-factor라고 불린다.

Figure 5: (SSD Algorithm.) state space model을 semiseparable matrix로 표현하는 행렬 변환 관점(Section 3)을 사용하여, SSD 모델의 하드웨어 효율적인 계산을 위한 block-decomposition 행렬 곱셈 알고리즘을 개발한다. 이 행렬 곱셈은 state space model로도 해석될 수 있으며, 여기서 블록들은 입력 및 출력 시퀀스의 chunking을 나타낸다. 대각 블록은 chunk 내 계산(intra-chunk computation)을 나타내고, 비대각 블록은 SSM의 hidden state를 통해 factorize된 chunk 간 계산(inter-chunk computation)을 나타낸다.

Right Factors. 이 단계에서는 low-rank factorization의 right B-block-factor에 의한 곱셈을 계산한다. 각 chunk에 대해 이는 (N, Q) x (Q, P) 행렬 곱셈이며, 여기서 N은 state dimension이고 P는 head dimension이다. 결과는 각 chunk에 대한 (N, P) tensor이며, 이는 확장된 hidden state $h$와 동일한 차원을 가진다.

이는 초기 상태(chunk에 대한)가 0이라고 가정할 때, chunk당 최종 상태가 무엇인지로 해석될 수 있다. 즉, 이는 $x_{0: j Q}=0$이라고 가정할 때 $h_{j Q+Q-1}$을 계산한다.

Center Factors. 이 단계에서는 low-rank factorization에서 center A-block-factor 항들의 효과를 계산한다. 이전 단계에서 chunk당 최종 상태는 총 (T/Q, N, P) 형태를 가진다. 이제 이것은 $A_{2 \mathrm{Q}-1: \mathrm{Q}-1}^{\times}, A_{3 \mathrm{Q}-1: 2 \mathrm{Q}-1}^{\times}, \ldots, A_{\mathrm{T}-1: \mathrm{T}-\mathrm{Q}-1}^{\times}$에 의해 생성된 1-SS 행렬과 곱해진다. 이 단계는 1-SS 곱셈(scalar SSM scan 또는 cumprodsum operator라고도 함)을 계산하는 모든 알고리즘으로 계산할 수 있다.

이는 이전의 모든 입력을 고려할 때 chunk당 실제 최종 상태가 무엇인지로 해석될 수 있다. 즉, 이는 $x_{0:(j+1) Q}$의 모든 것을 고려하여 실제 hidden state $h_{j Q}$를 계산한다.

Left Factors. 이 단계에서는 low-rank factorization의 left C-block-factor에 의한 곱셈을 계산한다. 각 chunk에 대해 이는 행렬 곱셈 $\operatorname{contract}(\mathrm{QN}, \mathrm{NP} \rightarrow \mathrm{QP})$으로 표현될 수 있다.

이는 올바른 초기 상태 $h_{j Q-1}$를 고려하고, 입력 $x_{j Q:(j+1) \mathrm{Q}}$가 0이라고 가정할 때 chunk당 출력이 무엇인지로 해석될 수 있다. 즉, chunk $j$에 대해 이는 이전 입력 $x_{0: j Q}$만을 고려하여 올바른 출력을 계산한다.

6.3 Computational Cost

우리는 BMM(B, M, N, K) 표기법을 사용하여 배치 차원 B를 갖는 batched matrix multiplication 계약 (MK, KN → MN) 을 정의한다. 이 표기법으로부터 효율성의 세 가지 측면을 추론할 수 있다:

• 계산 비용: 총 $O(\mathrm{BMNK})$ FLOPs.
• 메모리 비용: 총 $O(\mathrm{~B}(\mathrm{MK}+\mathrm{KN}+\mathrm{MN}))$ 공간.

Listing 1 Full PyTorch example of the state space dual (SSD) model.
def segsum(x):
    """Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
        which is equivalent to a scalar SSM."""
    T = x.size(-1)
    x_cumsum = torch.cumsum(x, dim=-1)
    x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
    mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
    x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
    return x_segsum
def ssd(X, A, B, C, block_len=64, initial_states=None):
    """
    Arguments:
        X: (batch, length, n_heads, d_head)
        A: (batch, length, n_heads)
        B: (batch, length, n_heads, d_state)
        C: (batch, length, n_heads, d_state)
    Return:
        Y: (batch, length, n_heads, d_head)
    assert X.dtype == A.dtype == B.dtype == C.dtype
    assert X.shape[1] % block_len == 0
    # Rearrange into blocks/chunks
    X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
    A = rearrange(A, "b c l h -> b h c l")
    A_cumsum = torch.cumsum(A, dim=-1)
    # 1. Compute the output for each intra-chunk (diagonal blocks)
    L = torch.exp(segsum(A))
    Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)
    # 2. Compute the state for each intra-chunk
    # (right term of low-rank factorization of off-diagonal blocks; B terms)
    decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
    states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)
    # 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries
    # (middle term of factorization of off-diag blocks; A terms)
    if initial_states is None:
        initial_states = torch.zeros_like(states[:, :1])
    states = torch.cat([initial_states, states], dim=1)
    decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
    new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
    states, final_state = new_states[:, :-1], new_states[:, -1]
    # 4. Compute state -> output conversion per chunk
    # (left term of low-rank factorization of off-diagonal blocks; C terms)
    state_decay_out = torch.exp(A_cumsum)
    Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)
    # Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
    Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")
    return Y, final_state

• 병렬화: 더 큰 $\mathrm{M}, \mathrm{N}, \mathrm{K}$ 항은 최신 가속기에서 특수 행렬 곱셈 장치(specialized matrix multiplication units) 를 활용할 수 있다.

Center Blocks. quadratic SMA 계산 비용은 세 단계로 구성된다 (Equation (16)):

• 커널 행렬 $C^{\top} B$ 계산: 비용은 $\mathrm{BMM}(\mathrm{T} / \mathrm{Q}, \mathrm{Q}, \mathrm{Q}, \mathrm{N})$이다.
• 마스크 행렬 곱셈: $(\mathrm{T} / \mathrm{Q}, \mathrm{Q}, \mathrm{Q})$ 형태의 텐서에 대한 요소별(elementwise) 연산이다.
• $X$ 값 곱셈: 비용은 $\mathrm{BMM}(\mathrm{T} / \mathrm{Q}, \mathrm{Q}, \mathrm{P}, \mathrm{N})$이다.

Low-Rank Blocks: Right Factors. 이 단계는 단일 행렬 곱셈이며, 비용은 $\mathrm{BMM}(\mathrm{T} / \mathrm{Q}, \mathrm{N}, \mathrm{P}, \mathrm{Q})$이다.

Low-Rank Blocks: Center Factors. 이 단계는 **길이 T/Q의 스칼라 SSM 스캔(또는 1-SS 곱셈)**이며, $(\mathrm{N}, \mathrm{P})$ 독립 채널에서 수행된다. 이 스캔의 작업량은 $\mathrm{TNP/Q}$로, 다른 요소들에 비해 무시할 수 있는 수준이다.

**블로킹(blocking)**으로 인해 시퀀스 길이가 $T$에서 $T/Q$로 줄어들기 때문에, 이 스캔은 순수 SSM 스캔(예: Mamba의 selective scan)보다 $Q$배 더 작은 비용을 가진다. 따라서 대부분의 문제 길이에서 다른 알고리즘(Appendix B)이 더 효율적이거나, 성능 저하 없이 훨씬 쉽게 구현될 수 있음을 관찰할 수 있다. 예를 들어, 1-SS 행렬 곱셈을 통한 이 방식의 naive 구현은 $\mathrm{BMM}(1, \mathrm{~T} / \mathrm{Q}, \mathrm{NP}, \mathrm{T} / \mathrm{Q})$의 비용을 가지며, 이는 구현이 훨씬 쉽고 naive recurrence/scan 구현보다 더 효율적일 수 있다.

Low-Rank Blocks: Left Factors. 이 단계는 단일 행렬 곱셈이며, 비용은 $\mathrm{BMM}(\mathrm{T} / \mathrm{Q}, \mathrm{Q}, \mathrm{P}, \mathrm{N})$이다.

총 비용 (Total Cost). 만약 $\mathrm{N}=\mathrm{P}=\mathrm{Q}$로 설정하면 (즉, 상태 차원, 헤드 차원, 청크 길이가 동일하면), 위의 모든 BMM 항은 $\mathrm{BMM}(\mathrm{T/N, N, N, N})$이 된다. 이 경우의 계산 특성은 다음과 같다:

• 총 FLOPs: $O\left(\mathrm{TN}^{2}\right)$.
• 총 메모리: $O(\mathrm{TN})$.
• 주요 작업: $(\mathrm{N}, \mathrm{N})$ 형태의 행렬에 대한 행렬 곱셈이다.

메모리 소비는 타이트하다는 점에 주목해야 한다; 입력 및 출력 $x, y$는 $(\mathrm{T}, \mathrm{P})=(\mathrm{T}, \mathrm{N})$ 형태를 가진다. 한편, FLOPs는 추가적인 N 인자를 반영하는데, 이는 autoregressive 상태 크기로 인해 발생하는 비용이며 모든 모델에 공통적으로 나타난다.

행렬 곱셈 외에도, $\mathrm{NP}=\mathrm{N}^{2}$개의 feature와 시퀀스 길이 $\mathrm{T} / \mathrm{Q}$에 대한 스칼라 SSM 스캔이 있다. 이는 $O\left(\mathrm{~T} / \mathrm{QN}^{2}\right)$ FLOPs와 $O(\log (\mathrm{~T} / \mathrm{Q}))$ 깊이를 가진다. 비록 행렬 곱셈을 사용하지는 않지만, 여전히 병렬화가 가능하며, 총 작업량은 다른 단계들에 비해 무시할 수 있는 수준이다. GPU 구현에서는 이 비용이 무시할 만하다.

순수 SSM 및 Attention 모델과의 비교 (Comparison to Pure SSM and Attention Models). Quadratic attention 또한 행렬 곱셈만을 활용하여 하드웨어 효율성이 매우 높지만, 총 FLOPs는 $T^{2} N$이다. 학습 및 추론 시 느린 계산 속도는 더 큰 상태 크기의 직접적인 결과로 볼 수 있다. 표준 attention은 이력을 캐싱하고 상태를 압축하지 않기 때문에 시퀀스 길이 $T$에 비례하는 상태 크기를 가진다.

Linear SSM은 $\mathrm{TNP} = \mathrm{TN}^{2}$의 총 FLOPs를 가지며, 이는 SSD와 동일하다. 그러나 naive 구현은 **추가 메모리를 구체화하는 상태 확장(15a)**과 **행렬 곱셈을 활용하지 않는 스칼라 연산(15b)**을 필요로 한다.

우리는 다른 특수 설정에 더 적합할 수 있는 SSD용 알고리즘으로 이어질 수 있는 다양한 행렬 분해(matrix decomposition)가 가능함을 언급한다 (예를 들어, Appendix B에서 다양한 구조화된 행렬 분해를 통한 1-SS 곱셈 알고리즘 모음 참조). 더 나아가, semiseparable matrix는 우리가 사용하는 SSS 형태(Definition 3.2) 외에도 풍부한 문헌과 더 많은 표현 방식을 가지고 있으며, 더 효율적인 알고리즘도 가능할 수 있음을 언급한다.

7 The Mamba-2 Architecture

SSM과 attention을 연결함으로써, SSD 프레임워크는 이 둘을 위한 공통된 어휘와 기술 라이브러리를 개발할 수 있게 해준다. 이 섹션에서는 원래 Transformer를 위해 개발된 아이디어를 사용하여 SSD layer를 이해하고 수정하는 몇 가지 예시를 논의한다. 우리는 Mamba-2 아키텍처를 도출하는 몇 가지 설계 선택 사항에 대해 논의한다. 이러한 변화 축은 Section 9.4에서 ablation된다.

Figure 6: (Mamba-2 아키텍처.) Mamba-2 블록은 순차적인 linear projection을 제거하여 Mamba 블록을 단순화한다. SSM 파라미터 $A, B, C$는 SSM 입력 $X$의 함수가 아니라 블록 시작 부분에서 생성된다. NormFormer (Shleifer, Weston, and Ott 2021)에서와 같이 추가적인 normalization layer가 추가되어 안정성을 향상시킨다. $B$와 $C$ projection은 multi-value attention (MVA)과 유사하게 $X$ 헤드 전체에서 공유되는 단일 헤드만을 가진다.

7.1 Block Design

우리는 먼저 내부 시퀀스 믹싱 레이어(즉, 핵심 SSD 레이어 외부)와 독립적인 신경망 블록 수정 사항에 대해 논의한다.

Parallel Parameter Projections (병렬 파라미터 투영)
Mamba-1은 selective SSM 레이어를 $X \mapsto Y$로 보는 SSM 중심의 관점에서 동기 부여되었다. SSM 파라미터 $A, B, C$는 보조적인 것으로 간주되며 SSM 입력 $X$의 함수이다. 따라서 $(A, B, C)$를 정의하는 선형 투영은 $X$를 생성하기 위한 초기 선형 투영 후에 발생한다.

Mamba-2에서는 SSD 레이어를 $A, X, B, C \mapsto Y$로 보는 관점을 취한다. 따라서 블록 시작 부분에서 단일 투영을 통해 $A, X, B, C$를 병렬로 생성하는 것이 합리적이다. 이는 표준 attention 아키텍처와 유사하며, 여기서 $X, B, C$는 병렬로 생성되는 $Q, K, V$ 투영에 해당한다.

SSM의 $A, B, C, X$ 입력에 대해 병렬 투영을 채택하면 파라미터 수가 약간 줄어들고, 더 중요하게는 표준 Megatron sharding 패턴(Shoeybi et al. 2019)을 사용하여 더 큰 모델에 대한 tensor parallelism에 더 적합하다는 점에 주목하라.

Extra Normalization (추가 정규화)
예비 실험에서 우리는 더 큰 모델에서 불안정성이 발생하기 쉽다는 것을 발견했다. 우리는 최종 출력 투영 바로 앞에 블록에 추가 정규화 레이어(예: LayerNorm, GroupNorm 또는 RMSNorm)를 추가하여 이를 완화할 수 있었다. 이러한 정규화 사용은 MLP 및 MHA 블록 끝에도 정규화 레이어를 추가한 NormFormer 아키텍처(Shleifer, Weston, and Ott 2021)와 가장 직접적으로 관련이 있다.

또한 이 변경 사항은 선형 attention 관점에서 파생된 Mamba-2와 관련된 다른 최신 모델들과 유사하다는 점에 주목한다. 원래의 선형 attention 공식은 표준 attention의 softmax 함수의 정규화를 모방하는 분모 항으로 정규화한다. TransNormerLLM (Qin, Dong Li, et al. 2023) 및 RetNet (Y. Sun et al. 2023)은 이 정규화가 불안정하다는 것을 발견하고 선형 attention 레이어 뒤에 추가 LayerNorm 또는 GroupNorm을 추가한다. 우리의 추가 정규화 레이어는 이들과 약간 다르며, multiplicative gate branch 이전에 발생하는 대신 이후에 발생한다.

7.2 Multihead Patterns for Sequence Transformations

SSM은 다음을 만족하는 **시퀀스 변환(Definition 2.1)**으로 정의된다는 점을 상기하자:

• $A, B, C$ 파라미터는 상태 차원(state dimension) N을 가진다.
• 이들은 $\mathbb{R}^{\top} \rightarrow \mathbb{R}^{\top}$ 형태의 시퀀스 변환을 정의하며, 예를 들어 행렬 $M \in \mathbb{R}^{(\top, \top)}$로 표현될 수 있다.
• 이 변환은 입력 시퀀스 $X \in \mathbb{R}^{(T, P)}$에 대해 P 축을 따라 독립적으로 동작한다.

이는 시퀀스 변환의 하나의 head를 정의하는 것으로 볼 수 있다. Definition 7.1 (Multihead patterns). Multihead 시퀀스 변환은 총 모델 차원 $\mathrm{D}=$ d_model에 대해 H개의 독립적인 head로 구성된다. 파라미터는 head 간에 공유될 수 있으며, 이는 head pattern으로 이어진다.

상태 크기 N과 head 차원 P는 각각 attention의 QK head 차원과 V head 차원에 해당한다. 최신 Transformer 아키텍처(Chowdhery et al. 2023; Touvron, Lavril, et al. 2023)에서와 마찬가지로, Mamba-2에서는 일반적으로 이들을 64 또는 128 정도의 상수로 설정한다. 모델 차원 D가 증가할 때, 우리는 head 차원 N과 P를 고정시킨 채 head의 수를 늘린다. 이를 설명하기 위해, multihead attention의 아이디어를 SSM 또는 모든 일반적인 시퀀스 변환에 적용하여 유사한 패턴을 정의하고 일반화할 수 있다.

Multihead SSM (MHS) / Multihead Attention (MHA) Pattern. 고전적인 MHA 패턴은 head 차원 P가 모델 차원 D를 나눈다고 가정한다. head의 수는 $H=D / P$로 정의된다. 그런 다음, 각 파라미터의 H개의 독립적인 복사본을 생성하여 핵심 시퀀스 변환의 H개의 복사본을 만든다. MHA 패턴은 attention 시퀀스 변환을 위해 처음 설명되었지만, Definition 2.1과 호환되는 모든 것에 적용될 수 있다는 점에 유의해야 한다. 예를 들어, multi-head SSD layer는 SSD 알고리즘이 $\mathrm{H}=\mathrm{n} \_$heads 차원에 걸쳐 broadcast되는 equation (17)에 따라 형태를 가진 입력을 수용할 것이다.

Multi-contract SSM (MCS) / Multi-query Attention (MQA) Pattern. Multi-query attention (Shazeer 2019)은 attention을 위한 영리한 최적화 기법으로, $K$ 및 $V$ 텐서를 캐싱하는 데 의존하는 autoregressive inference의 속도를 극적으로 향상시킬 수 있다. 이 기법은 단순히 $K$와 $V$에 추가적인 head 차원을 부여하는 것을 피하거나, 다른 말로 단일 (K, V) head를 Q의 모든 head에 걸쳐 broadcast한다.

**상태 공간 이중성(state space duality)**을 사용하여, 우리는 MQA의 등가 SSM 버전을 equation (18)로 정의할 수 있다. 여기서 $X$와 $B$ (attention의 $V$와 $K$에 해당하는 SSM 아날로그)는 $H$개의 head에 걸쳐 공유된다. 우리는 또한 이를 multi-contract SSM (MCS) head pattern이라고 부르는데, 이는 SSM 상태 수축을 제어하는 $C$ 파라미터가 head별로 독립적인 복사본을 가지기 때문이다.

유사하게, 우리는 multi-key attention (MKA) 또는 multi-expand SSM (MES) head pattern을 정의할 수 있다. 여기서 $B$ (SSM 확장을 제어)는 head별로 독립적인 반면, $C$와 $X$는 head에 걸쳐 공유된다.

Multi-input SSM (MIS) / Multi-value Attention (MVA) Pattern. MQA는 KV 캐시 때문에 attention에 적합하지만, SSM에는 자연스러운 선택이 아니다. Mamba에서는 대신 $X$가 SSM의 주요 입력으로 간주되며, 따라서 $B$와 $C$는 입력 채널에 걸쳐 공유되는 파라미터이다. 우리는 equation (20)에서 새로운 multi-value attention (MVA) 또는 multi-input SSM (MIS) 패턴을 정의하며, 이는 SSD와 같은 모든 시퀀스 변환에 다시 적용될 수 있다.

이러한 용어를 바탕으로, 우리는 원래 Mamba 아키텍처를 더 정확하게 특징지을 수 있다. Proposition 7.2. Mamba 아키텍처의 selective SSM (S6) layer (Gu and Dao 2023)는 다음을 가진 것으로 볼 수 있다:

• Head 차원 $P=1$: 모든 채널은 독립적인 SSM dynamics $A$를 가진다.
• Multi-input SSM (MIS) 또는 multi-value attention (MVA) head 구조: $B, C$ 행렬 (attention 이중성에서 $K, Q$에 해당)은 입력 $X$의 모든 채널 (attention에서 $V$에 해당)에 걸쳐 공유된다.

우리는 또한 SSD에 적용될 때 이러한 head pattern 변형을 ablation할 수 있다 (Section 9.4.3). 흥미롭게도, 파라미터 수와 총 상태 차원이 제어됨에도 불구하고, 다운스트림 성능에는 눈에 띄는 차이가 있다. 우리는 Mamba에서 원래 사용된 MVA 패턴이 가장 우수한 성능을 보인다는 것을 경험적으로 발견했다.

Grouped Head Patterns. Multi-query attention의 아이디어는 grouped-query attention (Ainslie et al. 2023)으로 확장될 수 있다: 1개의 K 및 V head 대신, $1<\mathrm{G}$이고 G가 H를 나누는 경우 G개의 독립적인 K 및 V head를 생성할 수 있다. 이는 multi-query attention과 multi-head attention 간의 성능 차이를 줄이고, 샤드 수의 배수로 G를 설정하여 더 효율적인 텐서 병렬화를 가능하게 하는 두 가지 동기에서 비롯된다 (Section 8).

유사하게, Mamba-2에서 사용된 multi-input SSM head pattern은 grouped-input SSM (GIS) 또는 동의어인 **grouped-value attention (GVA)**으로 쉽게 확장될 수 있다. 일반화는 간단하며, 우리는 단순화를 위해 세부 사항을 생략한다.

7.3 Other SSD Extensions from Linear Attention

여기서는 linear attention에서 영감을 받아 SSD에 적용한 아키텍처 수정의 한 예시를 설명한다. 우리는 이를 Section 9.4.3에서 negative result의 형태로 ablation 연구를 수행했으며, 기본 설정으로 채택할 만큼 성능 향상이 유의미하지 않음을 발견했다. 그럼에도 불구하고, 이러한 수정은 방대한 attention 관련 연구들이 SSD의 변형을 정의하는 데 어떻게 통합될 수 있는지를 보여준다. 우리는 Mamba-2 아키텍처에서 kernel feature map의 선택을 hyperparameter로 취급하며, attention에서 영감을 받은 다른 간단한 수정들도 가능할 것으로 예상한다.

Softmax Attention에 대한 Kernel Attention 근사 (Kernel Attention Approximations to Softmax Attention)
많은 linear attention 또는 kernel attention 변형들은 **attention score $\operatorname{softmax}\left(Q K^{\top}\right)$**를 다음과 같이 구성된 것으로 간주하여 동기를 부여받는다:

1. 지수 커널(exponential kernel) $Z=\exp \left(Q K^{\top}\right)$은 특정 kernel feature map에 대해 $Z=\psi(Q) \psi(K)^{\top}$로 근사될 수 있다.
2. 행 합계가 1이 되도록 커널을 정규화하는 과정 $M=G / G 11^{\top}$ (여기서 나눗셈은 element-wise로 이루어지며, 1은 모든 원소가 1인 벡터이다).

지수 커널 feature map (Exponential Kernel Feature Maps)
Mamba-2에서는 유연한 kernel feature map을 통합하고, 이를 **B 및 C 브랜치(attention의 K 및 V 브랜치에 해당)**에 적용한다. 이 feature map은 단순성과 대칭성을 위해 선택적으로 X(V) 브랜치에도 적용될 수 있다. 이는 Figure 6에서 임의의 비선형 함수로 표현된다. 기본적으로 우리는 $\psi$를 element-wise Swish / SiLU 함수로 선택한다 (Hendrycks and Gimpel 2016; Ramachandran, Zoph, and Le 2017). Section 9.4.3의 ablation 연구에서는 Linear Attention, Performer, Random Feature Attention, cosFormer (Section 4.1.3)에서 사용된 feature map을 포함한 다른 옵션들도 탐색한다.

정규화 (분모) 항 통합 (Incorporating a Normalization (Denominator) Term)
분모 항을 찾기 위해서는 단순히 M1을 계산해야 한다. 하지만 모델의 최종 출력은 $Y=M X$ (equation (16))임을 상기하라. 따라서 정규화 항은 X에 추가 열 1을 추가하여 (T, P+1) 형태의 텐서를 생성함으로써 간단히 찾을 수 있다.

이 경우, 합계가 양수가 되도록 kernel feature map $\psi$는 양수여야 한다는 점에 유의하라.

8 Systems Optimization for SSMs

우리는 SSM, 특히 Mamba-2 아키텍처에 대한 여러 시스템 최적화를 설명하며, 이는 대규모의 효율적인 학습 및 추론을 위한 것이다. 특히, 우리는 대규모 학습을 위한 tensor parallel 및 sequence parallel에 중점을 두며, 효율적인 fine-tuning 및 추론을 위한 가변 길이 시퀀스도 다룬다.

8.1 Tensor Parallel

Tensor parallelism (TP) (Shoeybi et al. 2019)은 각 layer(예: attention, MLP)를 여러 가속기(예: GPU)에서 실행되도록 분할하는 모델 병렬화 기법이다. 이 기법은 대부분의 대규모 모델(Brown et al. 2020; Chowdhery et al. 2023; Touvron, Lavril, et al. 2023; Touvron, L. Martin, et al. 2023)을 GPU 클러스터에서 학습시키는 데 널리 사용되며, 이 클러스터는 일반적으로 NVLink와 같은 고속 네트워킹을 갖춘 4-8개의 GPU를 포함하는 노드로 구성된다. TP는 원래 Transformer 아키텍처를 위해 개발되었으며, 다른 아키텍처에 적용하는 것이 간단하지 않다. 우리는 먼저 Mamba 아키텍처에서 TP를 사용하는 것의 어려움을 보여주고, 이어서 Mamba-2 아키텍처가 TP를 효율적으로 만들도록 어떻게 설계되었는지를 보여준다.

단일 입력 $u \in \mathbb{R}^{L \times d}$ (단순화를 위해 batching 없음), 입력 projection matrix $W^{(x)}, W^{(z)} \in \mathbb{R}^{d \times e d}$ (여기서 $e$는 확장 계수이며 일반적으로 2), 그리고 출력 projection matrix $W^{(o)} \in \mathbb{R}^{e d \times d}$를 갖는 Mamba 아키텍처를 상기해보자:

$$\begin{aligned} x & =u W^{(x)^{\top}} \in \mathbb{R}^{L \times e d} \\ z & =u W^{(z)^{\top}} \in \mathbb{R}^{L \times e d} \\ x_{c} & =\operatorname{conv} 1 \mathrm{~d}(x) \in \mathbb{R}^{L \times e d} \quad(\text { depthwise, independent along } d) \\ \Delta, B, C & =\text { low-rank projection }\left(x_{c}\right) \\ y & =S S M_{A, B, C, \Delta}\left(x_{c}\right) \in \mathbb{R}^{L \times e d} \quad \text { (independent along } d \text { ) } \\ y_{g} & =y \cdot \phi(z) \quad \text { (gating, e.g., with } \phi \text { being SiLU) } \\ \text { out } & =y_{g} W^{(o)^{\top}} \in \mathbb{R}^{L \times d} . \end{aligned}$$

TP를 사용하여 계산을 2개의 GPU로 분할한다고 가정해보자. 입력 projection matrix $W^{(x)}$와 $W^{(z)}$를 각각 $d \times \frac{e d}{2}$ 크기의 두 파티션으로 분할하는 것은 쉽다. 그러면 각 GPU는 $L \times \frac{e d}{2}$ 크기의 $x_{c}$ 절반을 보유하게 된다. 그러나 $\Delta, B, C$가 $x_{c}$의 함수이므로, $\Delta, B, C$를 계산하기 전에 $x_{c}$ 전체를 얻기 위해 GPU들 간에 추가적인 all-reduce가 필요하다. 그 후 두 GPU는 $d$ 차원을 따라 독립적이므로 SSM을 병렬로 계산할 수 있다. 마지막으로 출력 projection matrix $W^{(o)}$를 각각 $\frac{e d}{2} \times d$ 크기의 두 파티션으로 분할하고, 마지막에 all-reduce를 수행할 수 있다. Transformer와 비교할 때, 한 번의 all-reduce 대신 두 번의 all-reduce가 발생하여 통신에 소요되는 시간이 두 배가 된다. 대규모 Transformer 학습의 경우, 통신이 이미 상당한 시간(예: 10-20%)을 차지할 수 있으며, 통신 시간이 두 배가 되면 Mamba는 대규모 학습에 효율적이지 않게 된다.

Mamba-2의 목표는 Transformer의 attention 또는 MLP 블록과 유사하게 블록당 하나의 all-reduce만 갖는 것이다. 결과적으로, 우리는 $\Delta, B, C$를 $x_{c}$ 대신 $u$로부터 직접 얻는 projection을 사용하며, 이를 통해 이러한 projection matrix를 분할할 수 있다. 이는 다른 GPU에 다른 $\Delta, B, C$ 세트가 존재함을 의미하며, 이는 더 큰 "논리적 GPU"에 여러 "그룹"의 $\Delta, B, C$를 갖는 것과 동일하다. 또한, 우리는 각 블록 내에서 GroupNorm을 사용하며, 그룹 수는 TP degree로 나누어 떨어지도록 하여 TP 그룹 내의 GPU들이 블록 내에서 통신할 필요가 없도록 한다:

\begin{aligned} x & =u W^{(x)^{\top}} \in \mathbb{R}^{L \times e d} \\ z & =u W^{(z)^{\top}} \in \mathbb{R}^{L \times e d} \\ \Delta, B, C & =\operatorname{projection}(u) \quad(\text { one or more groups of } \Delta, B, C \text { per GPU }) \\ x_{c} & =\operatorname{conv} 1 \mathrm{~d}(x) \in \mathbb{R}^{L \times e d} \quad \text { (depthwise, independent along } d \text { ) \\ y & \left.=S S M_{A, B, C, \Delta}\left(x_{c}\right) \in \mathbb{R}^{L \times e d} \quad \text { (independent along } d\right) \\ y_{g} & =y \cdot \phi(z) \quad \text { (gating, e.g., with } \phi \text { being SiLU) } \\ y_{n} & =\operatorname{groupnorm}\left(y_{g}\right) \quad \text { (number of groups divisible by degree of tensor parallel) } \\ \text { out } & =y_{g} W^{(o)^{\top}} \in \mathbb{R}^{L \times d} \end{aligned}

우리는 입력 projection matrix와 출력 projection matrix만 분할하면 되고, 블록의 끝에서만 all-reduce를 수행하면 된다는 것을 알 수 있다. 이는 Transformer의 attention 및 MLP layer의 TP 설계와 유사하다. 특히, TP degree가 2인 경우, $W^{(x)}=\left[W_{1}^{(x)}, W_{2}^{(x)}\right]$ (여기서 $W_{i}^{(x)} \in \mathbb{R}^{d \times e d / 2}$), $W^{(z)}=\left[W_{1}^{(z)}, W_{2}^{(z)}\right]$ (여기서 $W_{i}^{(z)} \in \mathbb{R}^{d \times e d / 2}$),

Figure 7: (Mamba-2 블록의 병렬화.) (왼쪽: Tensor Parallelism) 우리는 입력 projection matrix $W^{(x)}, W^{(z)}$와 출력 projection matrix $W^{(o)}$를 분할한다. 각 SSM head $(A, B, C, X) \mapsto Y$는 단일 장치에 존재한다. 최종 normalization layer에 GroupNorm을 선택함으로써 추가 통신을 피한다. Transformer의 MLP 또는 attention 블록과 마찬가지로, layer당 하나의 all-reduce가 필요하다. (오른쪽: Sequence/Context Parallelism) SSD 알고리즘과 유사하게, 여러 장치를 사용하여 시퀀스 차원을 따라 분할할 수 있다. 각 장치는 시퀀스의 상태를 계산한 다음, 해당 상태를 다음 GPU로 전달한다.

그리고 $W^{(o)}=\left[\begin{array}{l}W_{1}^{(o)} \\ W_{2}^{(o)}\end{array}\right]$ (여기서 $W_{i}^{(o)} \in \mathbb{R}^{e d / 2 \times d}$)로 분할한다. $i=1,2$에 대해 TP Mamba-2 layer는 다음과 같이 작성될 수 있다:

$$\begin{aligned} x^{(i)} & =u W_{i}^{(x)^{\top}} \in \mathbb{R}^{L \times e d / 2} \\ z^{(i)} & =u W_{i}^{(z)^{\top}} \in \mathbb{R}^{L \times e d / 2} \\ \Delta^{(i)}, B^{(i)}, C^{(i)} & =\operatorname{projection}(u) \quad(\text { one or more groups of } \Delta, B, C \text { per GPU }) \\ x_{c}^{(i)} & =\operatorname{conv} 1 \mathrm{~d}\left(x^{(i)}\right) \in \mathbb{R}^{L \times e d / 2} \\ y^{(i)} & =S S M_{A, B, C, \Delta}\left(x_{c}^{(i)}\right) \in \mathbb{R}^{L \times e d / 2} \\ y_{g}^{(i)} & =y^{(i)} \cdot \phi\left(z^{(i)}\right) \\ y_{n}^{(i)} & \left.=\operatorname{groupnorm}^{(i)}\right) \quad \text { (number of groups divisible by degree of tensor parallel) } \\ \text { out }^{(i)} & =y_{g}^{(i)} W_{i}^{(o)^{\top}} \in \mathbb{R}^{L \times d / 2} \\ \text { out } & =\sum_{i} \text { out }^{(i)} \cdot \quad(\text { summing outputs from all GPUs with an all-reduce }) \end{aligned}$$

Mamba-2의 tensor parallel은 Figure 7 (왼쪽)에 설명되어 있다.

8.2 Sequence Parallelism

매우 긴 시퀀스의 경우, 입력과 activation을 시퀀스 길이 차원을 따라 다른 GPU로 분할해야 할 수 있다. 여기에는 두 가지 주요 기술이 있다:

1. Sequence parallelism (SP): residual 및 normalization 연산을 위한 기법으로, Korthikanti et al. (2023)에 의해 처음 제안되었다. 이 기술은 TP(Tensor Parallelism)에서의 all-reduce를 reduce-scatter와 all-gather로 분해한다. 동일한 TP 그룹 내의 모든 GPU에서 동일한 입력에 대해 residual 및 normalization 연산이 반복된다는 점에 착안하여, SP는 reduce-scatter, residual 및 normalization, 그리고 all-gather를 수행함으로써 activation을 시퀀스 길이 차원을 따라 분할한다.

   Mamba-2 아키텍처는 동일한 residual 및 normalization 구조를 사용하므로, SP는 수정 없이 적용된다.

2. Sequence parallelism for the token-mixing operations (attention 또는 SSM): "context parallelism (CP)"이라고도 알려져 있다. attention layer를 위한 여러 기술이 개발되었다 (예: Ring attention (Liu, Yan, et al. 2024; Liu, Zaharia,

Figure 8: (Multi-Query Associative Recall (MQAR)). Associative recall task는 recurrent state에 모든 관련 정보를 기억해야 하는 SSM에게 도전적인 과제이다. SSD layer는 개선된 아키텍처와 결합되어 Mamba-2에서 훨씬 더 큰 state size를 허용하며, 이는 Mamba-1 및 심지어 vanilla attention보다 훨씬 뛰어난 성능을 보인다.

and Abbeel 2023)), 정교한 load-balancing 기술 (Brandon et al. 2023)과 함께. attention에서의 sequence parallelism의 어려움은 query와 key를 블록으로 분할할 수 있지만, 각 query 블록이 key 블록과 상호작용해야 하므로 worker 수에 대해 quadratic한 통신 대역폭이 발생한다는 점이다.

SSM의 경우, 시퀀스를 간단한 방식으로 분할할 수 있다: 각 worker는 초기 state를 받아 자신의 입력에 대해 SSM을 계산하고, 최종 state를 반환하며, 그 최종 state를 다음 worker에게 전달한다. 이 경우 통신 대역폭은 worker 수에 대해 linear하다. 이러한 분해는 SSD 알고리즘 (Figure 5)에서 블록/청크로 분할하는 블록 분해와 정확히 동일하다. 우리는 Figure 7 (Right)에서 이 context parallelism을 설명한다.

8.3 Variable Length

사전학습 시에는 배치 내에서 동일한 시퀀스 길이를 사용하는 경우가 많지만, fine-tuning 또는 추론 시에는 모델이 길이가 다른 다양한 입력 시퀀스를 처리해야 할 수 있다. 이러한 경우를 처리하는 한 가지 단순한 방법은 배치 내의 모든 시퀀스를 최대 길이에 맞춰 **오른쪽으로 패딩(right-pad)**하는 것이지만, 시퀀스 길이가 크게 다를 경우 비효율적일 수 있다.

Transformer의 경우, 패딩을 피하고 GPU 간 로드 밸런싱을 수행하거나 (Zeng et al. 2022; Y. Zhai et al. 2023), 동일한 배치에 여러 시퀀스를 packing하고 attention mask를 조정하는 (Ding et al. 2024; Pouransari et al. 2024) 정교한 기술들이 개발되었다.

특히 SSM과 Mamba의 경우, 전체 배치를 하나의 긴 시퀀스로 처리하고 개별 시퀀스 간에 state를 전달하지 않음으로써 가변적인 시퀀스 길이를 처리할 수 있다. 이는 한 시퀀스의 끝에 있는 토큰 $t$에 대해 $A_t=0$으로 설정하여, 해당 토큰이 다른 시퀀스에 속하는 토큰 $t+1$로 정보를 전달하는 것을 방지하는 것과 동일하다.

9 Empirical Validation

우리는 Mamba-2를 순환 모델에 어려웠던 합성 recall task (Section 9.1)와 표준 언어 모델링 사전학습 및 다운스트림 평가 (Section 9.2)에서 경험적으로 평가한다. 우리의 SSD 알고리즘이 Mamba-1보다 훨씬 효율적이며 (Section 9.3), 중간 길이 시퀀스에서는 최적화된 attention과 견줄 만함을 검증한다. 마지막으로, Mamba-2 아키텍처의 다양한 설계 선택 사항에 대한 ablation을 수행한다 (Section 9.4).

9.1 Synthetics: Associative Recall

합성 연관 기억(associative recall) task는 언어 모델이 context 내에서 정보를 찾아내는 능력을 테스트하는 데 널리 사용되어 왔다. 일반적으로 이 task는 autoregressive 모델에 key-value 쌍의 연관 관계를 입력한 다음, 이전에 본 key를 보여주면 모델이 올바른 완성(completion)을 생성하도록 prompt를 주는 방식으로 진행된다. Multi-Query Associative Recall (MQAR) task는 모델이 여러 연관 관계를 기억하도록 요구하는 이 task의 특정 형식이다 (Arora, Eyuboglu, Timalsina, et al. 2024).
원래 Mamba 논문은 관련 합성 task, 특히 Selective Copying (Gu and Dao 2023) 및 Induction Heads (Olsson et al. 2022)에 대한 결과를 보고했는데, 이들은 더 쉬운 연관 기억 task로 볼 수 있다. MQAR task는 또한 "전화번호부 찾기(phonebook look-up)" task와 밀접하게 관련되어 있으며, 이는 SSM과 같은 recurrent 모델에게는 유한한 상태 용량(finite state capacity)으로 인해 어려운 것으로 나타났다 (De et al. 2024; Jelassi et al. 2024).

The Pile에서의 Scaling Laws (Sequence Length 8192)

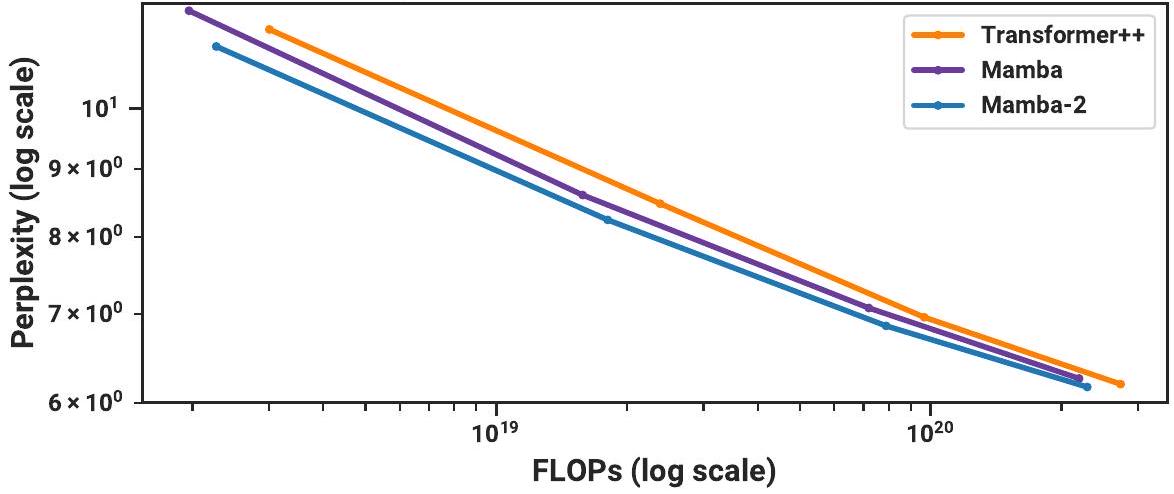
Figure 9: (Scaling Laws.) The Pile에서 학습된 약 125M에서 약 1.3B 파라미터 크기의 모델들. Mamba-2는 Mamba 및 강력한 "Transformer++" 레시피의 성능과 일치하거나 이를 능가한다. 우리의 Transformer baseline과 비교했을 때, Mamba-2는 성능(perplexity), 이론적 FLOPs, 실제 wall-clock time에서 Pareto dominant하다.

Table 1: (Zero-shot 평가.) 각 크기별 최고 결과는 굵게(bold), 두 번째 최고 결과는 밑줄(underline)로 표시되었다. 우리는 최대 300B 토큰으로 학습된 다양한 tokenizer를 사용하는 오픈 소스 LM과 비교한다. Pile은 validation split을 의미하며, 동일한 데이터셋과 tokenizer(GPT-NeoX-20B)로 학습된 모델만 비교한다. 각 모델 크기에서 Mamba-2는 Mamba를 능가하며, 일반적으로 Pythia의 두 배 모델 크기와 일치하는 성능을 보인다. 전체 결과는 Table 10에 있다.

Figure 10: (Efficiency Benchmarks.) (왼쪽) 우리의 SSD는 큰 state expansion (N=64)에서 Mamba의 fused scan보다 2-8배 빠르며, sequence length 2k 이상에서는 FlashAttention-2보다 빠르다. (오른쪽) Sequence length 4K: state expansion을 늘리면 Mamba의 최적화된 scan 구현이 선형적으로 느려진다. SSD는 훨씬 더 큰 state expansion factor를 큰 속도 저하 없이 처리할 수 있다.

우리는 (Arora, Eyuboglu, Zhang, et al. 2024)의 MQAR 설정 중 더 어려운 task, 더 긴 시퀀스, 더 작은 모델을 사용하여 도전적인 버전으로 비교한다. 우리의 baseline에는 표준 multi-head softmax attention과 convolution, local attention, linear attention 변형을 결합한 Based 아키텍처가 포함된다.

결과는 Figure 8에 나와 있다. Mamba-1은 이 task에서 어려움을 겪는 반면, Mamba-2는 모든 설정에서 좋은 성능을 보인다. 놀랍게도, state size가 제어될 때(N=16)에도 Mamba-1보다 훨씬 우수하다. (어떤 아키텍처 측면이 주요 요인인지는 확실하지 않으며, 이는 향후 연구에서 탐구할 질문으로 남아 있다.) 또한, 이 task는 state size의 중요성을 입증한다: N=16에서 N=64 및 N=256으로 증가시키면 MQAR 성능이 지속적으로 향상되는데, 이는 더 큰 state가 더 많은 정보(key-value 쌍)를 기억할 수 있도록 허용하기 때문이다.

9.2 Language Modeling

LLM의 표준 프로토콜에 따라, 우리는 Mamba-2 아키텍처를 다른 아키텍처들과 비교하여 표준 autoregressive language modeling에 대해 학습하고 평가한다. 우리는 **사전학습 지표(perplexity)**와 zero-shot 평가를 모두 비교한다. 모델 크기(깊이와 너비)는 GPT3 사양을 따르며, 125M부터 2.7B까지 다양하다. 우리는 **Pile 데이터셋 (L. Gao, Biderman, et al. 2020)**을 사용하고, Brown et al. (2020)에 설명된 학습 레시피를 따른다. 이는 Mamba (Gu and Dao 2023)에서 보고된 것과 동일한 설정이며, 학습 세부 사항은 Appendix D에 있다.

9.2.1 Scaling Laws

기준 모델로는 Mamba와 Transformer++ 레시피(Gu and Dao 2023)를 비교한다. Transformer++는 PaLM 및 LLaMa 아키텍처를 기반으로 하며, rotary embedding, SwiGLU MLP, LayerNorm 대신 RMSNorm, linear bias 없음, 더 높은 learning rate 등의 특징을 포함한다. Mamba는 이미 표준 Transformer 아키텍처(GPT3 아키텍처)뿐만 아니라 최근의 subquadratic 아키텍처들(H3 (Dao, D. Y. Fu, et al. 2023), Hyena (Poli et al. 2023), RWKV-4 (B. Peng, Alcaide, et al. 2023), RetNet (Y. Sun et al. 2023))보다 우수한 성능을 보였으므로, 명확성을 위해 해당 모델들은 그래프에서 생략한다 (비교 결과는 Gu and Dao (2023) 참조).

Figure 9는 Chinchilla (Hoffmann et al. 2022) 프로토콜에 따른 scaling law를 보여주며, 모델 크기는 약 1억 2천 5백만 개에서 약 13억 개 파라미터 범위이다.

9.2.2 Downstream Evaluations

Table 1은 Mamba-2가 다양한 인기 있는 다운스트림 zero-shot 평가 task에서 보여준 성능을, 해당 크기에서 가장 잘 알려진 오픈 소스 모델들, 특히 Pythia (Biderman et al. 2023)와 비교하여 보여준다. Pythia는 우리 모델과 동일한 **tokenizer, dataset, 학습 길이 (300B tokens)**로 학습되었다.

9.2.3 Hybrid Models: Combining SSD Layer with MLP and Attention

최근 및 동시 진행 연구(Dao, D. Y. Fu, et al. 2023; De et al. 2024; Glorioso et al. 2024; Lieber et al. 2024)에 따르면, SSM layer와 attention layer를 모두 포함하는 하이브리드 아키텍처가 Transformer 또는 순수 SSM(예: Mamba) 모델보다 모델 품질을 향상시킬 수 있으며, 특히 in-context learning에서 그러하다. 우리는 SSD layer가 attention 및 MLP와 결합될 수 있는 다양한 방식을 탐구하여 각 방식의 이점을 이해하고자 한다. 경험적으로 우리는 전체 layer 수의 약 10%가 attention layer일 때 가장 좋은 성능을 보인다는 것을 발견했다. 또한, SSD layer, attention layer, MLP를 결합하는 것이 순수 Transformer++ 또는 Mamba-2보다 더 나은 성능을 보인다.

SSD와 Attention
우리는 SSD와 attention layer가 상호 보완적임을 발견했다. 이들 각각만으로는(예: Mamba-2 아키텍처 vs. Transformer++) 성능(perplexity로 측정)이 거의 동일하지만, SSD와 attention layer의 혼합은 순수 Mamba-2 또는 Transformer++ 아키텍처보다 우수한 성능을 보인다. 우리는 GPT-2 tokenizer를 사용하여 Pile 데이터셋에서 7B 토큰으로 학습된 350M 모델(48개 layer)에 대한 일부 결과(Table 2)를 보여준다 (동일한 파라미터 수, 동일한 하이퍼파라미터, 동일한 학습 및 검증 세트). 단 몇 개의 attention layer를 추가하는 것만으로도 이미 주목할 만한 개선을 가져오며, 품질과 효율성 사이에서 최상의 균형을 이룬다. 우리는 SSM layer가 일반적인 sequence-to-sequence 매핑으로 잘 기능하고, attention layer는 모델이 모든 context를 메모리(SSM state)에 압축하도록 강제하는 대신 시퀀스 내 이전 토큰을 빠르게 참조하는 검색 메커니즘으로 작동한다고 가정한다.

Table 2: (SSD와 Attention 블록 결합.) 48개 layer를 가진 350M 모델의 perplexity, 다양한 attention layer 수에 따른 결과. attention layer 비율이 약 10%일 때 가장 좋은 성능을 보인다.

SSD, MLP, Attention을 포함하는 하이브리드 모델
우리는 SSD가 (gated) MLP 및 attention layer와 결합될 수 있는 다양한 방식을 비교하고, 2.7B 규모(64개 layer)에서 Pile 데이터셋으로 300B 토큰까지 학습된 모델을 평가한다 (동일한 파라미터 수, 동일한 하이퍼파라미터, 동일한 학습 및 검증 세트, 동일한 데이터 순서):

1. Transformer++: 32개의 attention layer와 32개의 gated MLP를 교차(interleaving) 배치.
2. Mamba-2: 64개의 SSD layer.
3. Mamba-2-MLP: 32개의 SSD와 32개의 gated MLP layer를 교차(interleaving) 배치.
4. Mamba-2-Attention: 58개의 SSD layer와 6개의 attention layer (인덱스 9, 18, 27, 36, 45, 56) .
5. Mamba-2-MLP-Attention: 28개의 SSD layer와 4개의 attention layer를 32개의 gated MLP layer와 교차(interleaving) 배치.

우리는 Pile 데이터셋에서의 검증 perplexity와 zero-shot 평가 결과를 Table 3에 보고한다. 일반적으로 Transformer++와 Mamba-2 모델의 품질은 거의 동일하다. 우리는 단 6개의 attention layer를 추가하는 것만으로도 순수 Mamba-2 모델(및 Transformer++)보다 성능이 현저히 향상됨을 확인했다. MLP layer를 추가하면 모델 품질이 저하될 수 있지만, (i) MLP layer의 단순성과 하드웨어 효율성 덕분에 학습 및 추론 속도를 높일 수 있고, (ii) MLP layer를 mixture-of-experts로 대체하여 MoE 모델로 쉽게 업사이클링할 수 있다.

Table 3: (Zero-shot 평가.) 각 크기별 최고 결과는 굵게 표시. Pile 데이터셋에서 300B 토큰까지 학습된 2.7B 규모 모델에서 SSD, MLP, attention layer가 결합될 수 있는 다양한 방식을 비교.

9.3 Speed Benchmarks

우리는 SSD 알고리즘의 속도를 Mamba의 scan 구현 및 FlashAttention-2와 비교 벤치마킹했다 (Figure 10). SSD는 행렬 곱셈을 서브루틴으로 사용하도록 재구성되었기 때문에, GPU의 특수 행렬 곱셈(matmul) 유닛(텐서 코어라고도 함)을 활용할 수 있다. 그 결과, matmul 유닛을 활용하지 않는 Mamba의 fused associative scan보다 2~8배 빠르다. 시퀀스 길이에 대한 선형 확장성 덕분에, SSD는 시퀀스 길이가 2K부터 FlashAttention-2보다 빠르다.

그러나 Mamba-2 모델 전체는 짧은 시퀀스 길이(예: 2K)에서 Transformer만큼 학습 효율적이지 않을 수 있다. 이는 $L$개의 layer를 가진 Transformer는 $\frac{L}{2}$개의 MLP layer와 $\frac{L}{2}$개의 attention layer를 가지는 반면, Mamba-2 모델은 동일한 수의 파라미터에 대해 $L$개의 SSD layer를 가지기 때문이다. 일반적으로 MLP layer는 단순한 행렬 곱셈과 pointwise linearity로 구성되어 하드웨어 효율성이 매우 높다. Section 9.2.3에서 보여주듯이, 짧은 시퀀스 길이에서 학습 속도를 높이기 위해 $\frac{L}{2}$개의 SSD layer와 $\frac{L}{2}$개의 MLP layer를 결합할 수도 있다.

Table 4: (Ablations: Mamba-2 block.) 우리는 Mamba-2와 Mamba-1 신경망 블록 간의 주요 차이점을 ablation 실험을 통해 분석했다 (Figure 6, Section 7.1). 이러한 구성 요소들은 내부 sequence mixing layer와는 독립적이다. 이 ablation 실험에서는 내부 SSM layer에 SSD를 사용했다 (Mamba-1의 S6 layer와 다름).

9.4 Architecture Ablations

9.4.1 Block Design

Section 7.1에서는 Mamba-2 block을 소개한다. 이 블록은 Mamba-1 block에 작은 수정 사항을 적용한 것으로, 이는 attention과의 연결성과 Mamba-2의 확장성 개선을 부분적으로 고려한 것이다. Table 4는 핵심 SSM layer 외부에서 발생하는 이러한 블록 아키텍처 변경 사항에 대한 ablation 결과를 보여준다.

ablation 결과는 (A, B, C, X)를 생성하기 위한 병렬 projection이 파라미터 수를 절약하고 Mamba의 순차적 projection보다 약간 더 나은 성능을 보인다는 것을 입증한다. 더 중요한 것은, 이러한 수정이 더 큰 모델 크기에서 tensor parallelism에 적합하다는 점이다 (Section 8). 또한, 추가적인 normalization layer도 성능을 약간 향상시킨다. 더 중요하게는, 더 큰 규모에서의 예비 실험에서 이 layer가 학습 안정성에도 도움이 된다는 것이 관찰되었다.

9.4.2 Head Structure

Section 7.2에서는 $B, C, X$ projection의 차원이 multi-head attention 및 multi-query attention 개념과 유사한 하이퍼파라미터로 간주될 수 있음을 설명한다. 또한 우리는 원래 Mamba 아키텍처가 multi-value attention과 유사하다는 것(Proposition 7.2)을 보였는데, 이는 state-space model 관점에서 자연스럽게 발전한 선택이었으며 이전에는 ablation 연구가 수행되지 않았다.

Table 5는 Mamba-2 아키텍처의 multi-head 구조 선택에 대한 ablation 결과를 보여준다. 놀랍게도, multi-value와 multi-query 또는 multi-key head 패턴 간에 큰 차이가 있음을 발견했는데, 이는 겉보기에는 매우 유사해 보임에도 불구하고 나타난 결과이다. 이는 총 state 크기(모든 경우에 HPN, 즉 헤드 수, 헤드 차원, state 차원의 곱과 동일)로 설명되지 않는다는 점에 주목해야 한다.

우리는 또한 $C, B, X$ (이는 $Q, K, V$와 유사함) 헤드의 수가 동일한 multi-head 패턴과도 비교한다. 표준 multi-head 패턴뿐만 아니라, 모든 헤드가 1개만 있는 공격적인 공유(aggressive sharing) 패턴과도 비교한다. 후자의 경우에도 모델은 여전히 H개의 다른 sequence mixer $M$을 가지는데, 이는 각 헤드가 여전히 다른 $A$를 가지기 때문이다. 파라미터 수가 일치할 때, 이러한 multi-head 패턴들은 MVA와 MQA/MKA 패턴의 중간 정도의 성능을 보이며 서로 유사하게 작동한다.

9.4.3 Attention Kernel Approximations

Section 7.3에서는 SSD가 다양한 형태의 kernel approximation과 같은 linear attention 문헌의 아이디어와 결합될 수 있음을 언급했다. 우리는 Table 6에서 이전 연구들이 제안한 이러한 변형들 중 몇 가지에 대해 ablation을 수행했다. 여기에는 cosFormer (Qin, Weixuan Sun, et al. 2022), Random Feature Attention (H. Peng et al. 2021), 그리고 Positive Random Features (Performer) (Choromanski et al. 2021)가 포함된다.

또한 우리는 표준 attention의 softmax 함수의 분모와 유사한 정규화 항을 추가하는 ablation도 수행했다. 그 결과, 대부분의 변형에서 불안정성을 야기했지만, ReLU activation function $\psi$의 성능을 약간 향상시키는 것을 발견했다.

Table 7은 feature dimension을 확장하는 방식을 포함하는 linear attention 개선을 위한 최신 제안들도 테스트한다 (Based (Arora, Eyuboglu, Zhang, et al. 2024) 및 ReBased (Aksenov et al. 2024)). 이러한 linear attention 확장은 quadratic approximation을 통해 exp kernel을 근사화하는 것을 목표로 한다. ReBased는 또한 QK activation function을 layer normalization으로 대체할 것을 제안한다. SSM 중심의 관점에서 우리는 SSM 함수를 적용하기 전에 $(B, C)$ 위에 normalization을 적용한다.

Table 5: (Ablations: Multi-head structure.) 모든 모델은 state expansion factor $N=64$ 및 **head size $P=64$**를 가지며, Chinchilla scaling law token count에 맞춰 학습되었다. $A$ head의 수는 항상 총 head 수 $H$와 동일하다. 즉, 각 head는 별도의 입력 의존적인 $A$ decay factor를 가진다. (상단) 125M 모델, 2.5B 토큰 (하단) 360M 모델, 7B 토큰

Table 6: (Ablations: Kernel approximations.) 우리는 kernel activation function $\psi$에 대한 다양한 제안을 테스트했으며, 여기에는 표준 softmax attention의 exp kernel을 근사화하려는 linear attention 변형이 포함된다.

Table 7: (Ablations: Kernel approximations.) 우리는 확장된 feature map을 포함하는 linear attention 근사화를 위한 (Re)Based 방법을 테스트한다. (상단) 130M 모델. (상단) $N=256$인 380M 모델.

이 기술은 softmax attention을 위한 "QK-Norm" (Team 2024) 및 Mamba를 위한 "internal normalization" (Lieber et al. 2024)으로 독립적으로 제안되었다는 점에 주목한다.

전반적으로 Table 6과 Table 7의 결과는 우리가 시도한 kernel approximation 방법들이 $\psi$에 대한 단순한 pointwise non-linear activation function보다 개선되지 않았음을 보여준다. 따라서 Mamba-2의 기본 설정은 Mamba-1을 따라 $\psi(x)=\operatorname{Swish}(x)$를 사용했지만, 이 activation을 완전히 제거하는 것이 우리가 광범위하게 테스트하지 않은 더 간단한 선택일 수 있다고 제안한다.

그러나 SSD와 vanilla linear attention은 1-semiseparable mask $L$의 포함 여부에서 차이가 있으며, 문헌의 다양한 linear attention 방법들은 이 항 없이 softmax attention을 근사화하기 위해 도출되었다는 점을 강조한다. 따라서 우리의 부정적인 결과는 예상치 못한 것이 아닐 수 있다.

10 Related Work and Discussion

State Space Duality (SSD) 프레임워크는 SSM, structured matrix, attention 간의 연결을 잇는다. 우리는 SSD와 이러한 개념들 간의 관계를 더 깊이 논의한다. 각 관점의 아이디어를 사용하여, 향후 연구에서 SSD 프레임워크가 확장될 수 있는 몇 가지 방향도 제안한다.

10.1 State Space Models

Structured state space model은 다음 축을 따라 특징지을 수 있다: (i) time-invariant인지 time-varying인지 여부. (ii) 시스템의 차원(dimensionality). (iii) recurrent transition $A$의 구조.

SSD는 SISO 차원과 scalar-identity 구조를 가진 selective SSM으로 설명될 수 있다. 시간 가변성 (Time Variance, Selectivity). 원래의 structured SSM (S4)은 continuous-time online memorization [Gu, Dao, et al. 2020; Gu, Johnson, Goel, et al. 2021; Gu, Johnson, Timalsina, et al. 2023]에 의해 동기 부여된 선형 시불변(LTI) 시스템이었다 [Gu 2023; Gu, Goel, and Ré 2022]. structured SSM의 많은 변형들이 제안되었으며 [Dao, D. Y. Fu, et al. 2023; Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Ma et al. 2023; J. T. Smith, Warrington, and Linderman 2023], 이 중 일부는 recurrence를 제거하고 LTI SSM의 convolutional representation에 초점을 맞추기도 했다 [D. Y. Fu et al. 2023; Y. Li et al. 2023; Poli et al. 2023; Qin, Han, Weixuan Sun, B. He, et al. 2023].

SSD는 time-varying structured SSM이며, Mamba [Gu and Dao 2023]에서 소개된 selective SSM으로도 알려져 있다. selective SSM은 LSTM [Hochreiter and Schmidhuber 1997] 및 GRU [J. Chung et al. 2014]와 같은 고전적인 RNN뿐만 아니라, QRNN [Bradbury et al. 2016], SRU [Lei 2021; Lei et al. 2017], RWKV [B. Peng, Alcaide, et al. 2023], HGRN [Qin, Yang, and Zhong 2023], Griffin [Botev et al. 2024; De et al. 2024]와 같은 최신 변형을 포함한 RNN의 gating mechanism과 밀접하게 관련되어 있다. 이러한 RNN들은 다양한 방식으로 parameterization이 다르지만, 가장 중요한 차이점은 state expansion의 부재이다.

차원 및 상태 확장 (Dimensionality and State Expansion). SSD의 중요한 특징은, 그 계보에 있는 이전 SSM들(S4, H3, Mamba)과 공유하는 것으로, 입력 채널이 독립적으로 처리되는 single-input single-output (SISO) 시스템이라는 점이다. 이는 ND라는 훨씬 더 큰 **유효 상태 크기(effective state size)**로 이어진다. 여기서 **N은 SSM의 state size (state expansion factor라고도 함)**이고 D는 표준 모델 차원이다. 전통적인 RNN은 N=1이거나, dense한 B, C 행렬을 가진 multi-input multi-output (MIMO) 시스템이며, 이 두 경우 모두 더 작은 상태 크기를 가진다. MIMO SSM이 일부 도메인에서 잘 작동하는 것으로 나타났지만 [Lu et al. 2023; Orvieto et al. 2023; J. T. Smith, Warrington, and Linderman 2023], Mamba는 언어와 같이 정보 밀도가 높은 도메인에서는 state expansion이 매우 중요함을 보여주었다. SSD의 주요 장점 중 하나는 모델 속도를 저하시키지 않으면서도 훨씬 더 큰 state expansion factor를 허용한다는 점이다. 이후 많은 후속 연구들이 state expansion을 채택했다 (Section 10.4).

구조 (Structure). 이전 structured SSM과 비교할 때, SSD의 주요 제약은 state transition $A_t$의 표현력에 있다. 우리는 diagonal $A_t$의 경우와 같은 더 일반적인 SSM이 SSD와 동일한 이론적 효율성을 가지지만, 하드웨어 친화적이지 않다는 점에 주목한다. 이는 dual quadratic form이 attention과 유사한 해석을 잃고 계산하기 더 어려워지기 때문이다. 따라서 Mamba와 비교할 때, SSD는 diagonal $A_t$의 형태가 약간 더 제한적이라는 점만 다르며, 향상된 하드웨어 효율성(및 구현 용이성)을 위해 이러한 표현력을 희생한다.

우리는 일반적인 diagonal SSM의 경우에도 structured matrix algorithm을 개선하는 것이 가능할 수 있다고 가정한다.

10.2 Structured Matrices

State space duality의 첫 번째 관점은 이러한 모델들을 행렬 시퀀스 변환(matrix sequence transformations) 또는 "행렬 믹서(matrix mixers)"로 간주한다. 이는 시퀀스 차원 $T$를 따라 **행렬 곱셈(T x T 행렬에 의한)**으로 표현될 수 있는 **시퀀스 변환(Definition 2.1)**이다.

이러한 행렬 믹서들은 이전에 여러 차례 제안되었으며, 주요 변형 축은 행렬의 표현 방식이다. 여기에는 MLP-Mixer (Tolstikhin et al. 2021) (비구조화된 행렬), FNet (Lee-Thorp et al. 2021) (Fourier Transform 행렬), M2 (Dao, B. Chen, et al. 2022; Dao, Gu, et al. 2019; Dao, Sohoni, et al. 2020; D. Fu et al. 2024) (butterfly/monarch 행렬), Toeplitz 행렬 (Poli et al. 2023; Qin, Han, Weixuan Sun, B. He, et al. 2023), 그리고 더 이색적인 구조들 (De Sa et al. 2018; Thomas et al. 2018)이 포함된다.

중요한 특징은 효율적인 (sub-quadratic) 행렬 시퀀스 변환이 구조화된 행렬 믹서를 가진 변환과 정확히 일치한다는 점이다. SSD 프레임워크의 핵심 결과는 SSM을 특정 구조, 즉 semiseparable 행렬(Section 3)을 가진 행렬 믹서로 보는 것이다. 이때 선형(linear) 대 이차(quadratic) 이중성은 구조화된 행렬 곱셈 대 단순 행렬 곱셈의 형태를 띤다.

구조 행렬 표현은 특정 **semiseparable 행렬의 블록 분해(block decompositions)**를 통해 **효율적인 SSD 알고리즘(Section 6)**으로 이어졌다. 우리는 semiseparable 행렬이 과학 계산 문헌에서 잘 연구되어 왔으며, 이러한 아이디어를 통합하는 것이 state space model의 추가 개선을 위한 유망한 길이 될 수 있음을 주목한다. 또한, 행렬 믹서 관점에 집중하는 것이 시퀀스 모델에 더 유익한 방향으로 이어질 수 있다고 제안한다. 예를 들어, Mamba의 원칙적인 비인과적(non-causal) 변형을 설계하거나, softmax attention과 sub-quadratic 모델 간의 간극을 특성화하고 연결하는 방법을 그들의 행렬 변환 구조 분석을 통해 찾는 것 등이 있다.

10.3 (Linear) Attention

표준 (causal) attention과 비교할 때, SSD는 단 두 가지 주요 차이점을 가진다. 첫째, SSD는 표준 attention의 softmax 활성화 함수를 사용하지 않는다 (Bahdanau, Cho, and Bengio 2015; Vaswani et al. 2017). 이 softmax가 attention의 quadratic complexity를 유발하는 원인이다. softmax를 제거하면, linear attention framework (Katharopoulos et al. 2020)를 통해 선형 스케일링으로 시퀀스를 계산할 수 있다.

둘째, SSD는 logits 행렬에 입력 의존적인 1-semiseparable mask를 곱한다. 따라서 이 mask는 표준 attention의 softmax를 대체하는 것으로 볼 수 있다.

이 semiseparable mask는 위치 정보(positional information)를 제공하는 것으로도 볼 수 있다. 요소 $a_t$는 RNN의 "gate" 또는 "선택(selection)" 메커니즘 (Mamba 논문의 논의 참조) 역할을 하며, 이들의 누적 곱 $a_{j:i}$는 위치 $i$와 $j$ 사이의 상호작용이 얼마나 허용되는지를 제어한다. Positional embedding (예: sinusoidal (Vaswani et al. 2017), AliBi (Press, N. Smith, and Lewis 2022), RoPE (Su et al. 2021))은 Transformer의 중요한 구성 요소이며 종종 **휴리스틱(heuristics)**으로 간주된다. SSD의 1-SS mask는 보다 원칙적인 형태의 relative positional embedding으로 볼 수 있다. 이러한 관점은 GateLoop (Katsch 2023)에서도 동시에 제시되었다.

state space duality의 두 번째 관점은 우리의 더 일반적인 structured masked attention (SMA) framework의 특수한 경우이다. 여기서 duality는 간단한 4-way tensor contraction에서 다른 contraction 순서로 나타난다. SMA는 linear attention의 강력한 일반화이며, SSD보다 훨씬 더 일반적이다. 다른 형태의 structured mask는 SSD와 다른 속성을 가진 더 많은 효율적인 attention 변형으로 이어질 수 있다.

새로운 모델로 이어지는 것 외에도, 이러한 attention과의 연결은 SSM을 이해하는 다른 방향으로 이끌 수 있다. 예를 들어, attention sink (Darcet et al. 2024; Xiao et al. 2024) 현상이 Mamba 모델에도 존재하는지, 그리고 더 나아가 interpretability 기술이 SSM으로 전이될 수 있는지 (Ali, Zimerman, and Wolf 2024) 궁금하다.

마지막으로, 많은 다른 linear attention 변형들이 제안되었으며 (Arora, Eyuboglu, Timalsina, et al. 2024; Arora, Eyuboglu, Zhang, et al. 2024; Choromanski et al. 2021; H. Peng et al. 2021; Qin, Han, Weixuan Sun, Dongxu Li, et al. 2022; Qin, Weixuan Sun, et al. 2022; Schlag, Irie, and Schmidhuber 2021; Zhang et al. 2024; Zheng, C. Wang, and Kong 2022) (이들 중 일부에 대한 설명은 Section 4.1.3 참조), 우리는 많은 기술들이 SSM으로 전이될 수 있을 것으로 예상한다 (예: Section 7.3).

우리는 SSD가 표준 softmax attention 또는 유한한 feature map $\psi$를 가지지 않는 attention kernel 행렬에 대한 다른 변환을 일반화하지 않는다는 점을 강조한다. 일반적인 attention과 비교할 때, SSD의 장점은 제어 가능한 state expansion factor N을 통해 이력을 압축한다는 점이다. 이는 시퀀스 길이 $T \gg N$에 따라 전체 이력을 캐시하는 quadratic attention과 대비된다. 동시 연구에서는 이러한 표현 방식의 trade-off를 연구하기 시작했으며, 예를 들어 복사(copying) 및 in-context learning task (Akyürek et al. 2024; Grazzi et al. 2024; Jelassi et al. 2024; Park et al. 2024)에서 이를 다루고 있다. Mamba-2가 이러한 일부 기능 (예: Section 9.1의 MQAR 결과에서 입증된 바와 같이)에서 Mamba보다 상당히 개선되었지만, 더 많은 이해가 필요하다.

10.4 Related Models

마지막으로, 우리는 Mamba 및 Mamba-2와 매우 유사한 시퀀스 모델을 개발한 최근 및 동시 연구들을 강조하고자 한다.

• RetNet (Y. Sun et al. 2023) 및 TransNormerLLM (Qin, Dong Li, et al. 2023)은 누적 합계 대신 decay term을 사용하여 Linear Attention을 일반화하고, 이중 병렬/재귀 알고리즘뿐만 아니라 하이브리드 "chunkwise" 모드를 제안한다. 이러한 알고리즘은 $A_t$가 시간 불변(모든 $t$에 대해 상수)인 SSD의 인스턴스로 볼 수 있다. SMA 해석에서는 마스크 행렬 $L$이 $L_{i,j} = \gamma^{i-j}$인 decay matrix가 될 것이다. 이 모델들은 또한 아키텍처적으로 다양한 방식으로 다르다. 예를 들어, 이들은 attention 중심의 관점에서 파생되었기 때문에 multi-head attention (MHA) 패턴을 유지한다. 반면 Mamba-2는 SSM 중심의 패턴에서 파생되었기 때문에 multi-value attention (MVA) 또는 multi-expand SSM (MES) 패턴을 유지하며, 우리는 이 패턴이 더 우수함을 보여준다 (Section 9.4).
• GateLoop (Katsch 2023)은 입력 의존적인 decay factor $A_t$를 사용하는 것을 동시에 제안했으며, SSD와 동일한 이중 이차 형식을 개발했는데, 이를 "surrogate attention" 형식이라고 부른다.
• Gated Linear Attention (GLA) (Yang et al. 2024)은 데이터 의존적인 gate를 가진 Linear Attention의 변형을 제안했으며, chunkwise 모드를 계산하는 효율적인 알고리즘과 하드웨어 인식 구현을 함께 제시했다.
• HGRN (Qin, Yang, and Zhong 2023)은 입력 의존적인 gate를 가진 RNN을 도입했으며, HGRN2 (Qin, Yang, Weixuan Sun, et al. 2024)에서는 state expansion을 통합하도록 개선되었다.
• Griffin (De et al. 2024) 및 RecurrentGemma (Botev et al. 2024)는 입력 의존적인 gating을 가진 RNN이 local attention과 결합될 때 강력한 최신 Transformer와 매우 경쟁력이 있음을 보여주었다. Jamba 또한 Mamba를 몇 개의 attention layer와 결합하는 것이 언어 모델링에서 매우 우수한 성능을 보임을 보여주었다 (Lieber et al. 2024).
• xLSTM (Beck et al. 2024)은 state expansion 및 기타 gating, normalization, stabilization 기술을 채택하여 xLSTM을 개선한다.
• RWKV(-4) (B. Peng, Alcaide, et al. 2023)는 다른 Linear Attention 근사(attention-free Transformer (S. Zhai et al. 2021))에 기반한 RNN이다. 최근에는 선택성(selectivity) 및 state expansion 개념을 채택하여 RWKV-5/6 (Eagle and Finch) 아키텍처로 개선되었다 (B. Peng, Goldstein, et al. 2024).

11 Conclusion

우리는 SSM과 attention 변형 모델 간의 개념적 간극을 연결하는, 잘 연구된 구조화된 행렬(structured matrices) 클래스에 기반한 이론적 프레임워크를 제안한다. 이 프레임워크는 최근 SSM(예: Mamba)이 Transformer만큼 언어 모델링에서 뛰어난 성능을 보이는 이유에 대한 통찰력을 제공한다. 또한, 우리의 이론적 도구는 SSM(그리고 잠재적으로 Transformer)을 개선하기 위한 새로운 아이디어를 제공하며, 이는 양측의 알고리즘 및 시스템 발전을 연결한다. 시연으로서, 이 프레임워크는 SSM과 structured attention의 교차점에 있는 새로운 아키텍처(Mamba-2)의 설계를 안내한다.

Acknowledgments

우리는 $\Delta$의 gradient를 수치적으로 안정적인 방식으로 효율적으로 계산하는 방법에 대한 제안을 해준 Angela Wu에게 감사한다. MQAR 실험에 도움을 준 Sukjun Hwang과 Aakash Lahoti에게도 감사한다.

A Glossary

Table 8: 표기법 및 용어 설명; 약어는 굵게 표시. (상단) 자주 사용되는 텐서 차원. (하단) 상태 공간 모델 또는 구조화된 마스크 어텐션에 사용되는 행렬 및 텐서.

B Efficient Algorithms for the Scalar SSM Scan (1-SS Multiplication)

이 섹션에서는 **구조화된 행렬 분해(structured matrix decomposition)**의 관점에서 스칼라 SSM scan을 계산하기 위한 다양한 알고리즘을 상세히 설명한다. 스칼라 SSM scan은 $N=1$일 때(즉, $A$가 스칼라일 때) 이산 SSM (7)의 재귀적인 부분을 계산하는 것으로 정의된다. 이는 SSM을 재귀적으로 계산하는 데 일반적으로 사용된다. 특히, $A$가 대각선 구조를 가지는 구조화된 SSM의 경우, 이 연산으로 귀결되며, S5 (J. T. Smith, Warrington, and Linderman 2023) 및 S6 (Gu and Dao 2023) 모델이 그 예시이다.

이 섹션의 목표는 시퀀스 모델을 위한 효율적인 알고리즘이 구조화된 행렬 곱셈 알고리즘으로 볼 수 있다는 본 논문의 핵심 주제를 뒷받침하는 것이다. 여기서 제시하는 다양한 행렬 분해(matrix decomposition) 아이디어는 고속 SSM 알고리즘(Section 6)을 도출하는 데 사용된 아이디어와 관련이 있으며, 서브루틴으로 직접 사용되기도 한다.

B. 1 Problem Definition

$a:(\mathrm{D},)$와 $b:(\mathrm{D},)$를 스칼라 시퀀스라고 하자. 스칼라 SSM scan은 다음과 같이 정의된다:

$$h_{t}=a_{t} h_{t-1}+b_{t} .$$

여기서 $h_{-1}$은 SSM recurrence의 이전 hidden state를 나타내는 임의의 값일 수 있다. 별도로 명시되지 않는 한, 우리는 $h_{-1}=0$으로 가정한다.

우리는 또한 식 (21)을 **cumprodsum (cumulative product sum)**이라고 부른다. cumprodsum은 $b=0$이 덧셈 항등원일 때 **cumprod (cumulative product)**으로 축소되며, $a=1$이 곱셈 항등원일 때 **cumsum (cumulative sum)**으로 축소된다는 점에 주목하라.

마지막으로, 벡터화된 형태로 다음과 같이 쓸 수 있다:

$$\begin{aligned} h & =M b \\ M & =\left[\begin{array}{ccccc} 1 & & & & \\ a_{1} & 1 & & & \\ a_{2} a_{1} & a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ a_{T-1} \ldots a_{1} & a_{T-1} \ldots a_{2} & \ldots & a_{T-1} & 1 \end{array}\right] \end{aligned}$$

다시 말해, 이는 단순히 1-SS 행렬 $M$과의 행렬-벡터 곱이다. 따라서 이 기본적인 primitive operation을 바라보는 세 가지 동등한 방식이 있다:

• (스칼라) SSM scan.
• cumprodsum.
• 1-SS 행렬-벡터 곱셈.

B. 2 Classical Algorithms

우리는 먼저 SSM scan (21)을 계산하는 두 가지 고전적인 방법을 설명한다. 이 방법들은 이전 연구들에서 사용되었다.

B.2.1 Sequential Recurrence

Recurrent 모드는 단순히 (21)을 한 번에 한 timestep $t$씩 계산한다. 1-SS 곱셈 관점에서는 이 내용이 Section 3.4.1에서도 설명되었다.

B.2.2 Parallel Associative Scan

둘째, 중요한 관찰은 이러한 재귀(recurrence)가 associative scan으로 변환될 수 있다는 점이다 (E. Martin and Cundy 2018; J. T. Smith, Warrington, and Linderman 2023). 이 사실은 완전히 명확하지는 않다. 예를 들어, S5는 올바른 associative scan operator를 정의한 다음, 기계적인 계산을 통해 operator의 결합성(associativity)을 보여주었다.

이것이 associative scan으로 계산 가능하다는 것을 보여주는 약간 더 깔끔한 방법은 다항 재귀(multi-term recurrence)를 1이 아닌 2 크기의 hidden state에 대한 단항 재귀(single-term recurrence)로 변환하는 것이다:

$$\begin{aligned} h_{t} & =a_{t} h_{t-1}+b_{t} \\ {\left[\begin{array}{c} h_{t} \\ 1 \end{array}\right] } & =\left[\begin{array}{cc} a_{t} & b_{t} \\ 0 & 1 \end{array}\right]\left[\begin{array}{c} h_{t-1} \\ 1 \end{array}\right] \end{aligned}$$

그러면 모든 $h_t$를 계산하는 것은 이 $2 \times 2$ 행렬들의 누적 곱(cumulative products)을 취하는 것과 동일하다. 행렬 곱셈은 결합적(associative)이므로, 이는 associative scan으로 계산될 수 있다. associative binary operator는 단순히 이 특정 행렬들에 대한 행렬 곱셈이다:

$$\left[\begin{array}{cc} a_{t} & b_{t} \\ 0 & 1 \end{array}\right]\left[\begin{array}{cc} a_{s} & b_{s} \\ 0 & 1 \end{array}\right]=\left[\begin{array}{cc} a_{t} a_{s} & a_{t} b_{s}+b_{t} \\ 0 & 1 \end{array}\right]$$

최상위 행을 동일시하면 S5가 정의한 것과 동일한 associative scan operator가 나온다:

$$\left(a_{t}, b_{t}\right) \otimes\left(a_{s}, b_{s}\right)=\left(a_{t} a_{s}, a_{t} b_{s}+b_{t}\right) .$$

associative scan이 중요한 이유는 divide-and-conquer 알고리즘(Blelloch 1990)을 사용하여 병렬화될 수 있기 때문이다. 우리는 이 알고리즘의 세부 사항은 생략하고, 대신 전체 associative SSM scan 알고리즘이 행렬 분해(matrix decompositions)를 통해 처음부터 유도될 수 있음을 보여준다 (Appendix B.3.5).

B. 3 Efficient Algorithms via Structured Matrix Decompositions

우리는 **1-SS 행렬 $M$의 구조화된 행렬 분해(structured matrix decomposition)**를 찾는 관점에서, SSM scan을 계산하기 위한 여러 알고리즘들을 논의한다. 이러한 알고리즘 또는 계산 모드에는 다음이 포함된다:

• Dilated mode: 정보가 한 번에 $1, 2, 4, 8, \ldots$ 단계씩 전파된다.
• State-passing mode: 정보가 청크(chunk) 단위로 순방향 전파된다.
• Fully recurrent mode: 한 번에 한 단계씩 증가하는 방식으로, state-passing mode의 특수한 경우이다.
• Block decomposition parallel mode: $M$이 계층적 블록으로 분할된다.
• Scan mode: $M$이 동일한 크기의 블록으로 분할되고 재귀적으로 축소된다.

B.3.1 Dilated Mode

이 모드는 증가하는 "stride"를 포함하는 특정 방식으로 1-SS 행렬을 인수분해한다. 이는 구체적인 예시를 통해 가장 잘 설명될 수 있다:

$$\begin{aligned} & M=\left[\begin{array}{llllllll} a_{0: 0} & & & & & & & \\ a_{1: 0} & a_{1: 1} & & & & & & \\ a_{2: 0} & a_{2: 1} & a_{2: 2} & & & & & \\ a_{3: 0} & a_{3: 1} & a_{3: 2} & a_{3: 3} & & & & \\ a_{4: 0} & a_{4: 1} & a_{4: 2} & a_{4: 3} & a_{4: 4} & & & \\ a_{5: 0} & a_{5: 1} & a_{5: 2} & a_{5: 3} & a_{5: 4} & a_{5: 5} & & \\ a_{6: 0} & a_{6: 1} & a_{6: 2} & a_{6: 3} & a_{6: 4} & a_{6: 5} & a_{6: 6} & \\ a_{7: 0} & a_{7: 1} & a_{7: 2} & a_{7: 3} & a_{7: 4} & a_{7: 5} & a_{7: 6} & a_{7: 7} \end{array}\right] \end{aligned}$$

이는 dilated convolution의 계산과 매우 유사하다는 점에 주목하라. 또한 이 인수분해는 1-SS 행렬이 butterfly 행렬의 특수한 경우임을 보여준다. butterfly 행렬은 또 다른 광범위하고 근본적인 유형의 구조화된 행렬이다 (Dao, Gu, et al. 2019; Dao, Sohoni, et al. 2020).

Remark 8. 이 알고리즘은 때때로 "work-inefficient하지만 더 병렬화 가능한(parallelizable)" prefix sum 알고리즘으로 설명된다 (Hillis and Steele fr 1986). 이는 $O(T \log (T))$ 연산을 사용하지만, work-efficient associative scan 알고리즘에 비해 depth/span이 절반이기 때문이다.

B.3.2 State-Passing (Chunkwise) Mode

이 모드는 표준 recurrent 모드의 일반화로 볼 수 있다. 표준 recurrent 모드에서는 recurrent state $h$를 한 번에 한 단계씩 전달하는 대신, 임의의 길이 $k$의 chunk에 대해 답을 계산하고 chunk를 통해 state를 전달한다. 이는 1-SS 행렬의 간단한 block decomposition으로부터도 유도될 수 있다.

Remark 9. 우리는 state가 한 local segment에서 다른 segment로 전달되는 방식을 지칭하기 위해 이를 "state-passing"이라고 부르지만, 이는 관련 모델들(Y. Sun et al. 2023; Yang et al. 2024)이 제안한 "chunkwise" 알고리즘과 관련이 있다. $h=M b$를 "chunk" 단위로 계산하는 것을 고려해보자: 특정 인덱스 $k \in[T]$에 대해, 우리는 $h_{0: k}$ 또는 인덱스 $k$까지의 출력을 계산하고 싶으며, 이 문제를 인덱스 $[k: T]$에 대한 더 작은 문제로 줄이는 방법을 가지고 있다.

$M$을 다음과 같이 쓸 수 있다:

$$M=\left[\begin{array}{ccccccc} a_{0: 0} & & & & & & \\ a_{1: 0} & a_{1: 1} & & & & & \\ \vdots & & \ddots & & & & \\ a_{k-1: 0} & \ldots & \ldots & a_{k-1: k-1} & & & \\ a_{k: 0} & \ldots & \ldots & a_{k: k-1} & a_{k: k} & & \\ \vdots & & & \vdots & \vdots & \ddots & \\ a_{T-1: 0} & \ldots & \ldots & a_{T-1: k-1} & a_{T-1: k} & \ldots & a_{T-1: T-1} \end{array}\right]$$

좌측 상단 삼각형을 $M_{L}$, 우측 하단 삼각형을 $M_{R}$ (좌측 및 우측 하위 문제), 좌측 하단 삼각형을 $M_{C}$라고 하자. $b$를 $b_{L}=b_{0: k}$와 $b_{R}=b_{k: T}$로 동일하게 나눈다. 다음을 주목하라:

$$M b=\left[\begin{array}{c} M_{L} b_{L} \\ M_{R} b_{R}+M_{C} b_{L} \end{array}\right]$$

또한, $M_{C}$는 rank-1 factorization을 가진다 (이는 본질적으로 semiseparable 행렬의 정의 속성이다):

$$M_{C}=\left[\begin{array}{c} a_{k: k} \\ \vdots \\ a_{T-1: k} \end{array}\right] a_{k}\left[\begin{array}{lll} a_{k-1: 0} & \cdots & a_{k-1: k-1} \end{array}\right]$$

따라서

$$M_{C} b_{L}=\left[\begin{array}{c} a_{k: k} \\ \vdots \\ a_{T-1: k} \end{array}\right] a_{k} \cdot(M b)_{k-1}$$

여기서 우리는 $(M b)_{k-1}=h_{k-1}$을 좌측 chunk의 "최종 state"로 간주한다. 왜냐하면 $M_{C}$의 factorization에 있는 행 벡터가 $M_{L}$의 마지막 행과 동일하기 때문이다. 또한, $M_{C}$의 factorization에 있는 열 벡터가 $M_{R}$의 마지막 열과 동일하다는 점에 주목하라.

$$M_{R} b_{R}+M_{C} b_{L}=M_{R}\left[\begin{array}{c} a_{k} h_{k-1}+b_{k} \\ b_{k+1} \\ \vdots \\ b_{T-1} \end{array}\right]$$

마지막으로, $M_{L}$과 $M_{R}$이 원래 행렬 $M$과 **자기 유사성(self-similar)**을 가진다는 관찰을 사용한다. 이 두 개의 더 작은 1-SS 행렬 곱셈에 대한 답은 어떤 알고리즘을 사용해서도 임의로 수행될 수 있다. 전체적으로, 알고리즘은 다음과 같이 진행된다:

1. 좌측 절반의 답 $h_{0: k}$를 원하는 방법으로 계산한다 (즉, 이 섹션의 1-SS 곱셈 방법 중 하나).
2. 최종 state $h_{k-1}$를 계산한다.
3. state를 한 단계 증가시켜 $b_{k}$를 수정한다.
4. 우측 절반의 답 $h_{k: T}$를 원하는 방법으로 계산한다.

다시 말해, 우리는 좌측 하위 문제를 블랙박스로 계산하고, 그 최종 state를 우측 문제로 전달하며, 우측 하위 문제를 블랙박스로 계산한다.

이 방법의 유용성은 더 복잡한 설정, 예를 들어 일반적인 $N$-semiseparable 경우나 입력 $b$가 추가적인 "batch" 차원을 가질 때 (즉, 행렬-벡터 곱셈 대신 행렬-행렬 곱셈일 때) 나타난다. 이 경우, 우리는 전체 hidden state $h$를 구체화하지 않는 chunk에 대한 대체 알고리즘 ( $M_{L}$ 및 $M_{R}$에 의한 MM에 해당)을 사용할 수 있다. 대신, 우리는 hidden state를 건너뛰고 최종 state $h_{k-1}$를 대체 방식으로 직접 계산한 다음, **state를 다음 chunk로 "전달"**한다.

Complexity. 이 방법은 2-3단계가 상수 시간만 소요되므로 매우 효율적일 수 있다. 따라서 두 하위 문제(1단계와 4단계)가 선형 시간이라고 가정하면, 전체 방법은 선형 시간을 소요한다.

단점은 이 또한 **순차적(sequential)**이라는 것이다.

B.3.3 Fully Recurrent Mode

Note that the fully recurrent mode, where the recurrence is evolved one step at a time (21), is simply an instantiation of the state-passing mode with chunk size $k=1$.

B.3.4 (Parallel) Block Decomposition Mode

이 방식은 state-passing 모드와 동일한 행렬 분해를 사용하지만, 병렬화를 위해 연산 순서를 다르게 하여 계산과 병렬화 간의 trade-off를 가진다.

일반적으로 $M$을 다음과 같이 나타낸다:

$$M=\left[\begin{array}{ccccc} 1 & & & & \\ a_{1} & 1 & & & \\ a_{2} a_{1} & a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ a_{T-1} \ldots a_{1} & a_{T-1} \ldots a_{2} & \ldots & a_{T-1} & 1 \end{array}\right]=\left[\begin{array}{ccccc} 1 & & & & \\ -a_{1} & 1 & & & \\ 0 & -a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ 0 & 0 & \ldots & -a_{T-1} & 1 \end{array}\right]^{-1}$$

핵심적인 관찰은 다시 한번 $M$의 좌하단 사분면이 rank-1이라는 점이다. 이를 확인하는 한 가지 방법은 직접 살펴보는 것이고, 다른 방법은 RHS를 사용하여 **RHS의 좌하단 사분면이 자명한 rank-1 행렬(우상단 모서리가 $-a_{T/2}$인 것을 제외하고 모두 0)**임을 관찰한 다음, Woodbury inversion formula를 사용하여 LHS의 좌하단 모서리도 rank 1이어야 함을 확인하는 것이다. 이는 또한 rank-1 factorization을 추론하는 방법을 제공하며, 이는 직접 확인을 통해 검증될 수 있다:

$$\begin{aligned} M_{\text {lower-left-quadrant }} & =\left[\begin{array}{ccc} \left(a_{T / 2} \ldots a_{1}\right) & \ldots & a_{T / 2} \\ \vdots & \ddots & \vdots \\ \left(a_{T-1} \ldots a_{T / 2} a_{T / 2-1} \ldots a_{1}\right) & \ldots & \left(a_{T-1} \ldots a_{T / 2}\right) \end{array}\right] \\ & =\left[\begin{array}{c} a_{T / 2} \\ \vdots \\ a_{T-1} \ldots a_{T / 2} \end{array}\right]\left[\left(a_{T / 2-1} \ldots a_{1}\right) \quad \ldots \quad a_{T / 2-1} \quad 1\right] . \end{aligned}$$

두 번째 관찰은 이 행렬이 **자기 유사성(self-similar)**을 가진다는 것이다: 어떤 principle submatrix도 동일한 형태를 가진다. 특히, 좌상단 및 우하단 사분면은 모두 1-SS 행렬이다. 이는 $M$에 의한 행렬 곱셈을 수행하는 쉬운 방법을 제공한다: 두 절반(즉, 좌상단과 우하단)에 대해 병렬로 재귀하고, 그 다음 좌하단 submatrix를 처리한다. divide-and-conquer 알고리즘에서 이 "조합(combination)" 단계는 submatrix가 rank 1이기 때문에 쉽다. 이는 병렬 알고리즘으로 이어진다.

복잡도 (Complexity)
state-passing 알고리즘과 마찬가지로, 이 방법은 rank-structured semiseparable matrix의 동일한 block decomposition을 사용한다. 차이점은 state-passing 알고리즘이 왼쪽 subproblem을 처리한 다음 오른쪽 subproblem을 처리하는 반면, 우리는 두 subproblem 모두에 대해 병렬로 재귀한다는 점이다. 이는 알고리즘의 depth/span을 선형에서 $\log(T)$로 낮춘다. trade-off는 조합 단계(rank-1 좌하단 submatrix를 처리하는 것)가 상수 작업 대신 선형 작업을 요구하므로, **총 작업량은 선형이 아닌 $O(T \log(T))$**가 된다.

또한, 재귀에서 언제든지 멈추고 다른 방식으로 subproblem을 계산할 수 있다는 점에 유의해야 한다. 이는 SSD 알고리즘(Section 6)의 주요 아이디어이며, 여기서는 작은 subproblem에 대해 dual quadratic attention formulation으로 전환한다.

B.3.5 Associative Scan Mode

state passing (chunkwise) 알고리즘은 선형적인 work를 가지지만, 순차적인 연산을 포함한다.

block matrix reduction과 dilated mode는 병렬화가 가능하며, $\log(T)$의 depth/span을 가진다. 하지만 이들은 추가적인 work($O(T \log(T))$)를 수행한다.

Appendix B.2.2에서 언급했듯이, associative scan (prefix scan이라고도 불림) 알고리즘을 활용하여 $O(\log T)$ depth와 $O(T)$ work를 모두 달성하는 알고리즘이 존재한다 (Baker et al. 1996). 이 알고리즘은 SSM scan 또는 cumprodsum 관점에서 가장 쉽게 이해할 수 있지만, 그럼에도 불구하고 명확하지는 않다. 이는 별도로 associative operator (22)를 도출한 다음, parallel/associative/prefix scan 알고리즘을 black box처럼 활용해야 한다 (Blelloch 1990).

여기서는 다른 행렬 분해를 활용하여 이 병렬 scan을 실제로 도출할 수 있음을 보여준다:

$$\begin{aligned} & M=\left[\begin{array}{ll|ll|ll|l} a_{0: 0} & & & & & & \\ a_{1: 0} & a_{1: 1} & & & & & \\ \hline a_{2: 0} & a_{2: 1} & a_{2: 2} & & & & \\ a_{3: 0} & a_{3: 1} & a_{3: 2} & a_{3: 3} & & & \\ \hline a_{4: 0} & a_{4: 1} & a_{4: 2} & a_{4: 3} & a_{4: 4} & & \\ a_{5: 0} & a_{5: 1} & a_{5: 2} & a_{5: 3} & a_{5: 4} & a_{5: 5} & \\ \hline a_{6: 0} & a_{6: 1} & a_{6: 2} & a_{6: 3} & a_{6: 4} & a_{6: 5} & a_{6: 6} \\ a_{7: 0} & a_{7: 1} & a_{7: 2} & a_{7: 3} & a_{7: 4} & a_{7: 5} & a_{7: 6} \end{array}\right] \\ & =\left\lvert\, \begin{array}{|cc|c|c|c|} \begin{array}{cc} a_{0: 0} & \\ a_{1: 0} & a_{1: 1} \end{array} & & & \\ \hline\left[\begin{array}{l} a_{2: 2} \\ a_{3: 2} \end{array}\right] a_{2: 1}\left[\begin{array}{l} a_{1: 0} \\ a_{1: 1} \end{array}\right]^{\top} & \begin{array}{l} a_{2: 2} \\ a_{3: 2} \end{array} & \begin{array}{l} a_{3: 3} \\ a_{3: 4} \end{array} & & \\ \hline\left[\begin{array}{l} a_{4: 4} \\ a_{5: 4} \end{array} a_{4: 1}\left[\begin{array}{l} a_{1: 0} \\ a_{1: 1} \end{array}\right]^{\top}\right. & {\left[\begin{array}{l} a_{4: 4} \\ a_{5: 4} \end{array}\right] a_{4: 3}\left[\begin{array}{l} a_{3: 2} \\ a_{3: 3} \end{array}\right]^{\top}} & a_{4: 4} & a_{5: 4} & a_{5: 5} \end{array}\right. \end{aligned}$$

이제 세 단계로 진행한다.

Stage 1. 먼저 곱셈 $M b$에서 각 대각 블록에 대한 해답을 계산한다. 이는 두 개의 숫자를 생성하지만, 첫 번째 요소는 변경되지 않는다. 예를 들어, 두 번째 블록은 $b_2$와 $a_3 b_2 + b_3$를 계산할 것이다.

Stage 2. 이제 행렬의 엄격한 하삼각 부분에서 rank-1 행렬로 인수분해된 각 $2 \times 2$ 블록을 고려한다. 각 오른쪽 행 벡터가 해당 열의 대각 블록에서 맨 아래 행 벡터와 동일하다는 점에 유의하라: 특히 $\left[\begin{array}{ll}a_{1: 0} & a_{1: 1}\end{array}\right]$, $\left[\begin{array}{ll}a_{3: 2} & a_{3: 3}\end{array}\right]$, 그리고 $\left[\begin{array}{ll}a_{5: 4} & a_{5: 5}\end{array}\right]$ 행들이다.

따라서 우리는 Stage 1에서 이미 이들에 대한 해답을 가지고 있으며, 이는 Stage 1의 모든 $T/2$ 하위 문제의 두 번째 요소이다. 이 요소들의 배열을 $b'$ ( $b$ 크기의 절반)이라고 부르면, 우리는 $b'$에 $a_{3:-1}, a_{3: 1}, a_{5: 3}, a_{7: 5}$에 의해 생성된 1-SS 행렬을 곱해야 한다.

Stage 3. 마지막으로, Stage 2의 각 해답은 왼쪽 열 벡터, 특히 $\left[\begin{array}{ll}a_{2: 2} & a_{3: 2}\end{array}\right]^{\top}$, $\left[\begin{array}{lll}a_{4: 4} & a_{5: 4}\end{array}\right]^{\top}$, 그리고 $\left[\begin{array}{ll}a_{6: 6} & a_{7: 6}\end{array}\right]^{\top}$ 벡터를 곱함으로써 두 개의 최종 해답으로 브로드캐스트될 수 있다.

이는 인덱스의 off-by-one shifting으로 약간 수정될 수 있다. 이 알고리즘을 보는 동등한 방법은 세 단계 행렬 분해로 보는 것이다.

$$\begin{aligned} & M=\left[\begin{array}{lllllll} a_{0: 0} & & & & & & \\ a_{1: 0} & a_{1: 1} & & & & & \\ a_{2: 0} & a_{2: 1} & a_{2: 2} & & & & \\ a_{3: 0} & a_{3: 1} & a_{3: 2} & a_{3: 3} & & & \\ a_{4: 0} & a_{4: 1} & a_{4: 2} & a_{4: 3} & a_{4: 4} & & \\ a_{5: 0} & a_{5: 1} & a_{5: 2} & a_{5: 3} & a_{5: 4} & a_{5: 5} & \\ a_{6: 0} & a_{6: 1} & a_{6: 2} & a_{6: 3} & a_{6: 4} & a_{6: 5} & a_{6: 6} \\ a_{7: 0} & a_{7: 1} & a_{7: 2} & a_{7: 3} & a_{7: 4} & a_{7: 5} & a_{7: 6} \end{array} a_{7: 7}\right] \end{aligned}$$

Stage 1과 Stage 3은 $O(T)$ work를 필요로 하는 반면, Stage 2는 크기가 절반인 자기 유사 문제로 축소된다. 이는 총 $O(T)$ work와 $O(\log T)$ depth/span을 필요로 함을 쉽게 확인할 수 있다. Remark 10. 사실, 이 알고리즘의 계산 그래프는 Appendix B.2.2에 설명된 associative scan 알고리즘의 계산 그래프와 동일하다는 것을 알 수 있다. 핵심은 (1) $M$이 재귀 관계를 정의한다는 것을 인식하고 (2) 재귀 관계가 associative 이항 연산자로 정의될 수 있음을 관찰하는 단계 대신, 단순히 $M$에 대한 구조화된 행렬 분해 알고리즘을 찾는 완전히 다른 관점이 있다는 것이다.

C Theory Details

C. 1 Extras: Closure Properties of SSMs

여기서는 semiseparable matrix의 유연성과 유용성을 보여주기 위해 몇 가지 추가적인 속성을 제시한다. 이 섹션은 우리의 핵심 결과를 이해하는 데 필수적이지는 않다.

Proposition C. 1 (Semiseparable Closure Properties). Semiseparable matrix는 여러 기본 연산에 대해 닫혀 있다.

• 덧셈(Addition): $N$-SS matrix와 $P$-SS matrix의 합은 최대 $(N+P)$-SS matrix이다.
• 곱셈(Multiplication): $N$-SS matrix와 $P$-SS matrix의 곱은 $(N+P)$-SS matrix이다.
• 역행렬(Inverse): $N$-SS matrix의 역행렬은 최대 $(N+1)$-SS matrix이다.

덧셈과 곱셈 속성은 쉽게 알 수 있다. 역행렬 속성은 여러 증명이 있으며, 한 가지 접근 방식은 Woodbury inversion identity에서 직접적으로 도출된다. 이 identity는 structured SSM 문헌에서도 중요하게 다루어져 왔다 (Gu, Goel, and Ré 2022).

이러한 속성들은 다시 **state space model (SSM)**의 closure 속성을 의미한다. 예를 들어, 덧셈 속성은 두 개의 병렬 SSM 모델을 합쳐도 여전히 SSM이라는 것을 말해준다. 곱셈 속성은 두 SSM을 순차적으로 합성하거나 연결하는 것이 여전히 SSM으로 간주될 수 있으며, 이때 총 state 크기는 가산적(additive)이라는 다소 비자명한 사실을 의미한다.

마지막으로, 역행렬 속성은 SSM을 다른 유형의 모델과 연결할 수 있게 해준다. 예를 들어, banded matrix는 semiseparable하다는 것을 알 수 있으며, 따라서 그 역행렬도 semiseparable하다. (실제로 semiseparable 구조군은 종종 banded matrix의 역행렬을 취하는 것으로부터 동기 부여된다 (Vandebril et al. 2005)). 더욱이, semiseparable matrix의 빠른 recurrence 속성은 그 역행렬이 banded하다는 것의 결과로 볼 수 있다.

Remark 11. 1-SS matrix가 단순한 recurrence (7)라는 사실은 1-SS matrix의 역행렬이 2-banded matrix라는 사실과 동등하다:

$$M=\left[\begin{array}{ccccc} 1 & & & & \\ a_{1} & 1 & & & \\ a_{2} a_{1} & a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ a_{T-1} \ldots a_{1} & a_{T-1} \ldots a_{2} & \ldots & a_{T-1} & 1 \end{array}\right]=\left[\begin{array}{ccccc} 1 & & & & \\ -a_{1} & 1 & & & \\ 0 & -a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ 0 & 0 & \ldots & -a_{T-1} & 1 \end{array}\right]^{-1}$$

따라서 $y=M x \leftrightarrow M^{-1} y=x$, 즉

$$\left[\begin{array}{ccccc} 1 & & & & \\ -a_{1} & 1 & & & \\ 0 & -a_{2} & 1 & & \\ \vdots & \vdots & \ddots & \ddots & \\ 0 & 0 & \ldots & -a_{T-1} & 1 \end{array}\right] y=x$$

또는 원소별로 보면,

$$\begin{aligned} & y_{t}-a_{t} y_{t-1}=x_{t} \\ & y_{t}=a_{t} y_{t-1}+x_{t} \end{aligned}$$

반대로, 우리는 이러한 closure 결과를 사용하여 autoregressive structured attention (특정 가정 하에)이 SSM이어야 함을 증명하고, 이를 통해 attention variant를 포함한 더 일반적인 효율적인 sequence model군이 state space model로 환원될 수 있음을 보여준다 (Appendix C.2).

C. 2 Autoregressive Masked Attention is Semiseparable-Structured Attention

Section 5.2의 Theorem 5.2를 증명한다. Section 4.3에서 우리는 structured attention을 masked attention의 광범위한 일반화로 정의했으며, 여기서 효율성(즉, kernel attention에 대한 선형 시간 형태)이라는 속성은 structured matrix multiplication의 효율성으로 추상화된다. 그러나 계산 효율성을 넘어, 표준 linear attention (Katharopoulos et al. 2020)은 두 가지 중요한 속성을 가진다. 첫째, **autoregressive modeling과 같은 설정에 필요한 인과성(causality)**을 가진다. 둘째, 효율적인 autoregressive generation이 가능하다. 즉, autoregressive step의 비용—$x_{0:T}$가 이미 처리되었고 $x_T$를 본 후 출력 $y_T$를 계산하는 증분 비용—은 상수 시간(constant time)만을 요구한다.

여기서는 SMA의 어떤 인스턴스가 효율적인 autoregression을 가지는지를 특성화한다. SMA 프레임워크에서 인과성(causality)은 마스크 $L$이 하삼각 행렬(lower-triangular matrix)이라는 제약과 동등하다. 효율적인 autoregression을 가지는 $L$ 행렬의 공간을 특성화하는 것은 더 어렵다. 우리는 시계열 문헌의 고전적인 정의(예: ARIMA 프로세스 (Box et al. 2015))의 정신에 따라 autoregressive 프로세스의 좁은 기술적 정의를 사용할 것이다. Definition C.2. 우리는 **차수(order) $k$의 autoregressive transformation $x \in \mathbb{R}^{T} \mapsto y \in \mathbb{R}^{T}$**를 각 출력 $y_t$가 현재 입력과 마지막 $k$개의 출력에만 의존하는 것으로 정의한다:

$$y_{t}=\mu_{t} x_{t}+\ell_{t 1} y_{t-1}+\cdots+\ell_{t k} y_{t-k}$$

$L$이 cumsum 행렬인 경우는 $k=1$인 특수한 경우이며, 따라서 $y_t = x_t + y_{t-1}$이다. 이 정의를 통해, 효율적인 autoregressive linear transform의 공간을 특성화하는 것은 semiseparable matrices의 속성으로부터 도출된다. Theorem C.3은 Theorem 5.2를 형식화하고 증명한다. Theorem C.3. $L \in \mathbb{R}^{T \times T}$가 차수 $k$의 효율적인 autoregressive transformation이라고 하자. 그러면 $L$은 차수 $k+1$의 state space model이다.

증명. $(x, y)$를 입력 및 출력 시퀀스라고 하자. 즉, $y=Lx$이다. 정의 (23)을 재배열하면,

$$y_{t}-\ell_{t 1} y_{t-1}-\cdots-\ell_{t k} y_{t-k}=\mu_{t} x_{t}$$

$t$에 대해 벡터화하면, 이는 행렬 변환으로 표현될 수 있다:

$$\left[\begin{array}{cccccc} 1 & & & & & \\ -\ell_{t 1} & 1 & & & & \\ \vdots & \ddots & \ddots & & & \\ -\ell_{t k} & \cdots & -\ell_{t 1} & 1 & & \\ \vdots & \ddots & \vdots & \ddots & \ddots & \\ 0 & \cdots & -\ell_{T-1, k} & \cdots & -\ell_{T-1,1} & 1 \end{array}\right]\left[\begin{array}{c} y_{0} \\ y_{1} \\ \vdots \\ y_{k} \\ \vdots \\ y_{T-1} \end{array}\right]=\left[\begin{array}{llllll} \mu_{0} & & & & & \\ & \mu_{1} & & & & \\ & & \ddots & & & \\ & & & \mu_{k} & & \\ & & & & \ddots & \\ & & & & & \mu_{T-1} \end{array}\right]\left[\begin{array}{c} x_{0} \\ x_{1} \\ \vdots \\ x_{k} \\ \vdots \\ x_{T-1} \end{array}\right]$$

$\mu$ 대각 행렬은 왼쪽으로 이동하여 $\ell$ 계수 행렬에 통합될 수 있으며, 이는 여전히 $k+1$-band 하삼각 행렬로 남는다. 그러나 우리는 또한 $L^{-1}y=x$를 가지므로, $L$은 이 행렬의 역행렬이다.

다음으로, $k+1$-band 행렬은 semiseparability의 랭크 특성화(Definition 3.1)에 의해 $k+1$-semiseparable이다. Proposition C.1에 의해, 역행렬 $L$은 따라서 최대 $k+2$-semiseparable이다. banded matrices의 추가적인 구조 때문에 $k+1$의 약간 더 강한 bound를 얻을 수 있다. 마지막으로, $L$이 차수 $k+1$의 state space model이라는 특성화는 Theorem 3.5로부터 도출된다.

즉, 효율적인 autoregressive attention은 semiseparable SMA이다.

D Experimental Details

D. 1 MQAR Details

우리는 Based (Arora, Eyuboglu, Zhang, et al. 2024)에서 소개된 task의 더 어려운 버전을 사용한다. 이 버전에서는 query/key/value가 아닌 token들이 무작위 token으로 대체된다. 또한, 기존 연구에서 사용된 일반적인 MQAR 변형보다 더 많은 key-value 쌍, 더 긴 시퀀스, 그리고 더 작은 모델 크기를 사용하는데, 이 모든 요소들이 task를 더 어렵게 만든다.

각 시퀀스 길이 $T \in\{256, 512, 1024\}$에 대해, 우리는 $T/4$개의 key-value 쌍을 사용한다. 전체 vocab size는 8192이다. 우리는 커리큘럼 학습(curriculum training) 방식을 사용하며, 학습은 $(T/32, T/16, T/8, T/4)$개의 key-value 쌍을 사용하는 데이터셋들을 순환한다. 각 데이터셋은 $2^{18} \approx 250000$개의 예시를 포함하며, 각 데이터셋을 총 8 epoch 동안 학습한다 (총 $2^{28} \approx 2억 7천만 개의 예시). 전체 batch size는$2^{18} \approx 0.25M$token이다 (예:$T=1024$일 때 batch size는 256이다).

모든 방법은 기본 설정으로 2개의 layer를 사용한다. attention baseline은 추가적으로 positional embedding을 받는다. 각 방법에 대해, 우리는 모델 차원 $D=\{32, 64, 128, 256\}$과 learning rate $\left\{10^{-3.5}, 10^{-2}, 10^{-2.5}\right\}$를 탐색한다. 우리는 매 epoch마다 learning rate가 감소하는 선형 decay schedule을 사용한다 (예: 마지막 epoch의 learning rate는 최대/시작 learning rate의 1/8이 된다).

D. 2 Scaling Law Details

모든 모델은 The Pile 데이터셋으로 학습되었다. scaling law 실험을 위해 GPT2 tokenizer를 사용한다.

모델 크기 (Model Sizes)
Table 9는 GPT3 (Brown et al. 2020)를 따라 scaling law 실험에 사용된 모델 크기를 명시한다. 첫째, 균일성을 위해 1.3B 모델의 batch size를 1M token에서 0.5M token으로 변경하였다. 둘째, 학습 token 수가 모델 크기에 비례하여 증가해야 한다는 Chinchilla scaling law (Hoffmann et al. 2022)에 대략적으로 맞추기 위해 학습 step 수와 총 token 수를 변경하였다.

학습 방식 (Training Recipes)
모든 모델은 AdamW optimizer를 사용했으며, 다음 설정을 따른다:

• gradient clip value 1.0
• weight decay 0.1
• no dropout
• cosine decay를 동반한 linear learning rate warmup

Table 9: (Scaling Law 모델 크기.) Scaling 실험을 위한 모델 크기 및 하이퍼파라미터. (모델 차원 및 head 수는 Transformer 모델에만 적용된다.)

기본적으로 peak learning rate는 GPT3의 사양을 따른다. GPT3 방식과 비교하여, 우리는 **PaLM (Chowdhery et al. 2023) 및 LLaMa (Touvron, Lavril, et al. 2023)와 같은 인기 있는 대형 language model에서 채택된 변경 사항에서 영감을 받은 "개선된 방식(improved recipe)"**을 사용한다. 여기에는 다음이 포함된다:

• $1e-5$까지 cosine decay를 동반한 linear learning rate warmup, peak 값은 GPT3 값의 5배
• linear bias term 없음
• LayerNorm 대신 RMSNorm 사용
• AdamW 하이퍼파라미터 $\beta=(.9, .95)$ (GPT3 값), PyTorch 기본값인 $\beta=(.9, .999)$ 대신 사용

D. 3 Downstream Evaluation Details

완전히 학습된 모델의 다운스트림 성능을 평가하기 위해, 우리는 GPTNeoX (Black et al. 2022) tokenizer를 사용하여 Pile 데이터셋의 300B 토큰으로 Mamba-2를 학습시켰다.

우리는 scaling 실험과 동일한 하이퍼파라미터를 사용했으며, 단 1.3B 및 2.7B 모델의 경우 batch size를 1M으로 설정했다. 2.7B 모델의 경우, GPT3 사양(32 layers, dimension 2560)을 따랐다.

모든 모델에 대해, 우리는 해당 GPT3 모델의 learning rate보다 5배 높은 learning rate를 사용했다. 다운스트림 평가를 위해, 우리는 **EleutherAI의 LM evaluation harness (L. Gao, Tow, et al. 2021)**를 사용했으며, Mamba (Gu and Dao 2023)와 동일한 task에 한 가지를 추가하여 평가했다:

• LAMBADA (Paperno et al. 2016)
• HellaSwag (Zellers et al. 2019)
• PIQA (Bisk et al. 2020)
• ARC-challenge (P. Clark et al. 2018)
• ARC-easy: ARC-challenge의 쉬운 subset
• WinoGrande (Sakaguchi et al. 2021)
• OpenBookQA (Mihaylov et al. 2018)

D. 4 Ablation Details

(Re)Based 세부 사항. Section 9.4.3의 ablation 연구에서는 Based (Arora, Eyuboglu, Zhang, et al. 2024) 및 ReBased (Aksenov et al. 2024) 모델을 고려했다.

Based는 $\exp$ 커널을 이차 Taylor 전개 $\exp (x) \approx 1+x+x^{2} / 2$로 근사하며, 이는 다음 feature map을 통해 구현될 수 있다:

$$\psi_{\text {Taylor }}(x)=\operatorname{concatenate}(1, x, 1 / \sqrt{2} x \otimes x) .$$

ReBased는 더 간단한 feature map인 $\psi_{\text {Quadratic }}(x)=x \otimes x$를 사용하여 $x^{2}$ 커널 변환에 대응시키지만, 그 전에 layer normalization을 적용한다. 우리는 이 layer normalization을 기본 Swish activation에 대한 대안적인 비선형 활성화로 간주하고, 이들의 조합을 ablation 연구에서 다룬다.

Table 10: (Zero-shot 평가.) 각 크기별 최고 결과는 굵게(bold), 두 번째 최고 결과는 밑줄(underline)로 표시했다. 우리는 최대 300B 토큰으로 학습된 다양한 tokenizer를 사용하는 오픈 소스 LM들과 비교했다. Pile은 validation split을 의미하며, 동일한 데이터셋과 tokenizer(GPT-NeoX-20B)로 학습된 모델하고만 비교했다. 각 모델 크기에서 Mamba-2는 Mamba보다 우수하며, 일반적으로 Pythia의 두 배 모델 크기와 비슷한 성능을 보인다.

이러한 방식들은 feature 차원을 확장하기 때문에, 더 작은 $B, C$ 차원으로 project해야 한다. Table 7에서는 130M 모델에 대해 **state size $N=64$**를, 380M 모델에 대해 **$N=256$**을 사용한다. (Re)Based 방법의 경우, feature map을 적용하기 전에 각각 8차원과 16차원으로 project한다. 그 결과, 130M 모델의 경우 **ReBased는 총 state size가 $8^{2}=64$**가 되고, **Based는 $1+8+8^{2}=73$**이 된다. $B$ 및 $C$ projection이 더 작기 때문에, 이 방법들은 더 적은 파라미터를 사용하며, 우리는 그에 따라 layer 수를 조정한다.