Mamba: 선택적 상태 공간을 이용한 선형 시간 시퀀스 모델링
Mamba는 Transformer의 긴 시퀀스에 대한 계산 비효율성을 해결하기 위해 제안된 Structured State Space Models (SSMs) 기반의 아키텍처입니다. 기존 SSM의 약점인 content-based reasoning 능력 부재를 해결하기 위해, 입력에 따라 SSM 파라미터가 동적으로 변하는 selection mechanism을 도입했습니다. 이를 통해 모델은 시퀀스를 따라 정보를 선택적으로 전파하거나 잊을 수 있습니다. 또한, 이로 인해 기존의 효율적인 convolution 연산을 사용할 수 없게 되는 문제를 하드웨어 친화적인 병렬 스캔 알고리즘으로 해결했습니다. Mamba는 attention이나 MLP 블록 없이 단순화된 종단 간 신경망 아키텍처로, 빠른 추론 속도와 시퀀스 길이에 대한 선형적인 확장성을 가지며 언어, 오디오, 유전체 등 다양한 데이터에서 SOTA 성능을 달성했습니다. 논문 제목: Mamba: Linear-Time Sequence Modeling with Selective State Spaces
논문 요약: Mamba: Linear-Time Sequence Modeling with Selective State Spaces
- 논문 링크: arXiv:2312.00752 (2023)
- 저자: Albert Gu (Carnegie Mellon University), Tri Dao (Princeton University)
- 발표 시기: 2023년, arXiv preprint
- 주요 키워드: State Space Model, Sequence Modeling, LLM, NLP, Multimodal, Mamba
1. 연구 배경 및 문제 정의
- 문제 정의:
현재 대규모 파운데이션 모델의 핵심인 Transformer 아키텍처는 긴 시퀀스에 대해 계산 비효율성(시퀀스 길이에 대한 이차적 스케일링)과 유한한 컨텍스트 윈도우라는 근본적인 단점을 가진다. 기존의 선형 시간 복잡도를 가진 아키텍처(선형 어텐션, 게이티드 컨볼루션, 순환 모델, Structured State Space Model (SSM) 등)들은 Transformer의 계산 비효율성을 해결하고자 했으나, 언어와 같이 정보 밀도가 높은 이산적인 모달리티에서는 어텐션만큼의 성능을 보여주지 못했다. 이는 기존 모델들이 콘텐츠 기반 추론(content-based reasoning) 능력이 부족했기 때문이다. - 기존 접근 방식:
Transformer는 self-attention을 통해 컨텍스트 윈도우 내에서 정보를 밀도 있게 라우팅하는 능력으로 복잡한 데이터를 모델링하지만, 유한한 윈도우 외부를 모델링할 수 없고 윈도우 길이에 대해 이차적으로 스케일링되는 단점이 있다. Structured State Space Model (SSM)은 순환 신경망(RNN)과 컨볼루션 신경망(CNN)의 조합으로 해석될 수 있으며, 시퀀스 길이에 대해 선형 또는 거의 선형적인 스케일링을 보여 효율적이다. 또한 장거리 종속성 모델링에 강점을 보였으나, 텍스트와 같은 이산적이고 정보 밀도가 높은 데이터에서는 덜 효과적이었다. 이는 기존 SSM이 선형 시간 불변성(Linear Time Invariance, LTI) 제약으로 인해 입력에 따라 정보를 선택적으로 처리하지 못했기 때문이다.
2. 주요 기여 및 제안 방법
- 논문의 주요 기여:
- 선택 메커니즘(Selection Mechanism) 도입: SSM 파라미터를 입력의 함수로 설정하여 모델이 현재 토큰에 따라 시퀀스를 따라 정보를 선택적으로 전파하거나 망각할 수 있도록 하여, 콘텐츠 기반 추론 능력을 부여했다.
- 하드웨어 친화적 병렬 스캔 알고리즘 개발: 선택 메커니즘으로 인해 기존의 효율적인 컨볼루션 연산을 사용할 수 없게 되는 문제를 해결하기 위해, GPU 메모리 계층 구조를 활용하는 효율적인 순환 모드(recurrent mode) 병렬 스캔 알고리즘을 설계했다.
- 단순화된 종단 간 신경망 아키텍처(Mamba) 제안: 어텐션이나 MLP 블록 없이 selective SSM을 통합한 간결하고 균일한 아키텍처를 제안하여, 빠른 추론 속도와 시퀀스 길이에 대한 선형적인 확장성을 달성했다.
- 제안 방법:
- 선택 메커니즘(Selection Mechanism): SSM의 핵심 파라미터인 를 입력 의 함수로 동적으로 생성한다. 이를 통해 모델은 시퀀스 내에서 관련 없는 정보를 필터링하고 관련 정보를 무기한으로 기억할 수 있게 된다. 이는 RNN의 게이팅 메커니즘을 일반화한 것으로 해석될 수 있다.
- 효율적인 구현 (Selective Scan): 선택 메커니즘으로 인해 SSM이 시간 가변(time-varying)이 되어 컨볼루션으로 계산할 수 없게 되므로, 순환 모드에서 효율적인 계산을 위해 하드웨어 인식 알고리즘을 사용한다. 이는 커널 퓨전(kernel fusion), 병렬 스캔(parallel scan), 재연산(recomputation)의 세 가지 기술을 활용하여 GPU의 HBM(고대역폭 메모리)과 SRAM(빠른 온칩 메모리) 간의 IO를 최소화하고, 중간 상태를 저장하지 않고 역전파 시 재계산하여 메모리 효율성을 극대화한다.
- Mamba 아키텍처: 기존 H3 아키텍처와 MLP 블록의 설계를 단순화하여 단일 Mamba 블록으로 통합한다. 이 블록은 모델 차원을 확장하는 선형 투영과 내부 SSM으로 구성되며, 표준 정규화 및 잔차 연결과 함께 반복적으로 쌓아 올려 Mamba 아키텍처를 형성한다.
3. 실험 결과
- 데이터셋:
- 합성 태스크: Selective Copying, Induction Heads (시퀀스 길이 256, 어휘 크기 16).
- 언어 모델링: The Pile 데이터셋 (GPT-2/GPT-NeoX 토크나이저).
- DNA 모델링: HG38 데이터셋 (단일 인간 게놈).
- 오디오 모델링: YouTubeMix (사전학습), SC09 (음성 생성 벤치마크).
- 주요 결과:
- 합성 태스크: Mamba는 Selective Copying 및 Induction Heads 태스크를 완벽하게 해결했으며, 특히 Induction Heads에서는 학습 시 본 시퀀스 길이보다 4000배 긴 백만 길이 시퀀스까지 완벽하게 외삽하는 능력을 보였다. 다른 어텐션 모델들은 2배 이상 일반화하지 못했다.
- 언어 모델링: Mamba는 Pile 데이터셋에서 다른 모든 어텐션-프리 모델보다 더 잘 확장되며, 특히 긴 시퀀스 길이에서 Transformer++ 레시피(PaLM, LLaMa 기반)의 성능과 일치하는 최초의 모델이다. 다운스트림 제로샷 평가에서 Mamba-3B 모델은 동일 크기의 Transformer를 능가하고, 두 배 크기의 Transformer(Pythia-7B)와 동등하거나 더 나은 성능을 보였다.
- DNA 모델링: Mamba는 HG38 데이터셋 사전학습에서 HyenaDNA 및 Transformer++보다 적은 파라미터로 더 잘 스케일링되었다. 또한, 1M에 달하는 극도로 긴 시퀀스에서도 긴 컨텍스트를 활용하여 사전학습 perplexity가 향상되었으며, 이는 컨텍스트 길이가 길어질수록 성능이 저하되는 HyenaDNA와 대조된다. 5가지 유인원 종 분류 다운스트림 태스크에서 Mamba는 7M 파라미터 모델로 81.31%의 높은 정확도를 달성했다.
- 오디오 모델링: YouTubeMix 사전학습에서 Mamba는 SaShiMi(S4+MLP)보다 전반적으로 우수했으며, 길이가 길어질수록 그 격차가 벌어졌다. SC09 음성 생성 벤치마크에서 작은 Mamba 모델(6.1M 파라미터)은 기존 SOTA GAN 및 Diffusion 기반 모델들을 능가하는 FID 0.94를 달성했으며, 더 큰 Mamba 모델(24.3M 파라미터)은 FID 0.67로 성능을 더욱 향상시켰다.
- 효율성: Mamba의 핵심 연산인 선택적 스캔은 시퀀스 길이 2K를 넘어서면 FlashAttention-2보다 빠르며, PyTorch 표준 스캔 구현보다 최대 20-40배 빠르다. Mamba는 Transformer보다 4-5배 높은 추론 처리량을 달성하며, KV 캐시가 없어 훨씬 높은 배치 사이즈를 사용할 수 있다. 메모리 사용량은 FlashAttention-2를 사용한 최적화된 Transformer 구현과 유사하다.
4. 개인적인 생각 및 응용 가능성
- 장점:
- Transformer의 고질적인 문제인 긴 시퀀스에 대한 이차적 계산 복잡도를 선형 시간으로 해결하면서도, Transformer에 필적하거나 능가하는 성능을 달성했다는 점이 가장 인상 깊다.
- 선택 메커니즘을 통해 기존 SSM의 약점이었던 콘텐츠 기반 추론 능력을 획기적으로 개선한 아이디어가 뛰어나다.
- 하드웨어 친화적인 알고리즘 설계로 이론적 효율성을 실제 GPU 환경에서의 빠른 속도와 낮은 메모리 사용량으로 구현해냈다는 점이 실용적이다.
- 언어, 오디오, 유전체 등 다양한 모달리티에서 SOTA 성능을 달성하여 범용 시퀀스 모델로서의 잠재력을 입증했다.
- 단점/한계:
- 현재 실험적 평가는 주로 7B 파라미터 미만의 모델 크기에 국한되어 있어, Llama와 같은 훨씬 더 큰 규모의 LLM에서 Mamba가 여전히 비교 우위를 가질지는 추가적인 검증이 필요하다.
- 연속적인 데이터 모달리티(예: 오디오)에서는 LTI(선형 시간 불변) SSM이 더 유리할 수 있다는 점이 흥미로운 한계점으로, 선택 메커니즘이 항상 이점을 제공하는 것은 아님을 시사한다.
- SSM의 대규모 확장에 추가적인 엔지니어링 문제 및 모델 조정이 필요할 수 있다는 점은 향후 연구 과제이다.
- 응용 가능성:
- 현재 Transformer 기반 LLM의 학습 및 추론 효율성 문제를 해결하여, 더 길고 복잡한 시퀀스를 처리하는 차세대 LLM의 핵심 백본으로 활용될 수 있다.
- 유전체학, 오디오, 비디오와 같이 매우 긴 컨텍스트를 요구하는 새로운 모달리티에서 파운데이션 모델을 구축하는 데 광범위하게 적용될 수 있다.
- 실시간 음성 처리, 긴 DNA 시퀀스 분석, 고해상도 비디오 생성 등 다양한 실제 애플리케이션에서 혁신을 가져올 수 있다.
5. 추가 참고 자료
Gu, Albert, and Tri Dao. "Mamba: Linear-time sequence modeling with selective state spaces." arXiv preprint arXiv:2312.00752 (2023).
Mamba: Linear-Time Sequence Modeling with Selective State Spaces
Albert Gu** and Tri Dao*²<br>¹ Machine Learning Department, Carnegie Mellon University<br> Department of Computer Science, Princeton University<br>agu@cs.cmu.edu, tri@tridao.me
Abstract
Foundation Model은 현재 딥러닝 분야의 가장 흥미로운 애플리케이션 대부분을 구동하고 있으며, 거의 보편적으로 Transformer 아키텍처와 핵심 attention 모듈에 기반하고 있다. **선형 attention, gated convolution 및 recurrent model, structured state space model (SSM)**과 같은 많은 subquadratic-time 아키텍처들이 긴 시퀀스에서 Transformer의 계산 비효율성을 해결하기 위해 개발되었지만, 언어와 같은 중요한 modality에서는 attention만큼의 성능을 보여주지 못했다.
우리는 이러한 모델들의 주요 약점이 콘텐츠 기반 추론(content-based reasoning)을 수행할 수 없다는 점을 파악하고, 몇 가지 개선 사항을 제안한다. 첫째, SSM 파라미터를 입력의 함수로 설정하는 것만으로도 이산적인 modality에서의 약점을 해결하여, 현재 토큰에 따라 시퀀스 길이 차원을 따라 정보를 선택적으로 전파하거나 망각할 수 있게 한다. 둘째, 이러한 변경이 효율적인 convolution 사용을 방해함에도 불구하고, 우리는 recurrent 모드에서 하드웨어 인지 병렬 알고리즘을 설계한다. 우리는 이러한 selective SSM을 attention이나 MLP 블록이 없는 단순화된 end-to-end 신경망 아키텍처(Mamba)에 통합한다.
Mamba는 **빠른 추론(Transformer보다 5배 높은 처리량)**과 시퀀스 길이에 대한 선형 확장성을 가지며, 백만 길이 시퀀스까지 실제 데이터에서 성능이 향상된다. 일반적인 시퀀스 모델 backbone으로서 Mamba는 언어, 오디오, 유전체학 등 여러 modality에서 state-of-the-art 성능을 달성한다. 언어 모델링에서 우리의 Mamba-3B 모델은 동일 크기의 Transformer를 능가하며, 두 배 크기의 Transformer와 동등한 성능을 보여준다. 이는 사전학습 및 다운스트림 평가 모두에서 확인되었다.
1 Introduction
Foundation Model (FM), 즉 대규모 데이터로 사전학습된 후 다운스트림 task에 맞춰 조정되는 대규모 모델은 현대 머신러닝에서 효과적인 패러다임으로 부상했다. 이러한 FM의 핵심은 종종 시퀀스 모델이며, 언어, 이미지, 음성, 오디오, 시계열, 유전체학 등 다양한 도메인의 임의의 입력 시퀀스에 대해 작동한다 (Brown et al. 2020; Dosovitskiy et al. 2020; Ismail Fawaz et al. 2019; Oord et al. 2016; Poli et al. 2023; Sutskever, Vinyals, and Quoc V Le 2014). 이 개념은 특정 모델 아키텍처 선택에 구애받지 않지만, 현대 FM은 주로 단일 유형의 시퀀스 모델인 Transformer (Vaswani et al. 2017)와 그 핵심 attention layer (Bahdanau, Cho, and Bengio 2015)에 기반을 두고 있다. self-attention의 효율성은 context window 내에서 정보를 밀도 있게 라우팅하는 능력에 기인하며, 이를 통해 복잡한 데이터를 모델링할 수 있다. 그러나 이러한 특성은 근본적인 단점을 가져온다: 유한한 window 외부를 모델링할 수 없다는 점과 window 길이에 대해 이차적으로 증가하는 스케일링이다. 이러한 단점을 극복하기 위해 더 효율적인 attention 변형에 대한 방대한 연구가 진행되었지만 (Tay, Dehghani, Bahri, et al. 2022), 종종 효과적인 특성 자체를 희생하는 경우가 많았다. 현재까지 이러한 변형 중 어느 것도 도메인 전반에 걸쳐 대규모로 경험적으로 효과적임이 입증되지 않았다.
최근, structured state space sequence model (SSM) (Gu, Goel, and Ré 2022; Gu, Johnson, Goel, et al. 2021)은 시퀀스 모델링을 위한 유망한 아키텍처 클래스로 부상했다. 이 모델들은 고전적인 state space model (Kalman 1960)에서 영감을 받아 recurrent neural network (RNN)와 convolutional neural network (CNN)의 조합으로 해석될 수 있다. 이 모델 클래스는 recurrence 또는 convolution으로 매우 효율적으로 계산될 수 있으며, 시퀀스 길이에 대해 선형 또는 거의 선형적인 스케일링을 보인다. 또한, 특정 데이터 양식에서 장거리 종속성을 모델링하기 위한 원칙적인 메커니즘을 가지고 있으며 (Gu, Dao, et al. 2020), Long Range Arena와 같은 벤치마크에서 우수한 성능을 보였다.
[^0] (Tay, Dehghani, Abnar, et al. 2021). 다양한 종류의 SSM (Gu, Goel, and Ré 2022; Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Y. Li et al. 2023; Ma et al. 2023; Orvieto et al. 2023; Smith, Warrington, and Linderman 2023)은 오디오 및 비전과 같은 연속 신호 데이터 도메인에서 성공적이었다 (Goel et al. 2022; Nguyen, Goel, et al. 2022; Saon, Gupta, and Cui 2023). 그러나 텍스트와 같이 이산적이고 정보 밀도가 높은 데이터를 모델링하는 데는 덜 효과적이었다.
우리는 새로운 selective state space model 클래스를 제안한다. 이 모델은 시퀀스 길이에 대해 선형적으로 스케일링하면서 Transformer의 모델링 능력을 달성하기 위해 기존 연구의 여러 측면을 개선한다.
Selection Mechanism. 첫째, 우리는 기존 모델의 주요 한계를 식별했다: 입력에 따라 데이터를 효율적으로 선택하는 능력 (즉, 특정 입력에 집중하거나 무시하는 능력)이다. selective copy 및 induction heads와 같은 중요한 합성 task에 기반한 직관을 바탕으로, 우리는 입력에 따라 SSM 파라미터를 매개변수화하여 간단한 selection mechanism을 설계한다. 이를 통해 모델은 관련 없는 정보를 필터링하고 관련 정보를 무기한으로 기억할 수 있다.
Hardware-aware Algorithm. 이러한 간단한 변경은 모델 계산에 기술적인 문제를 야기한다. 사실, 모든 기존 SSM 모델은 계산 효율성을 위해 시간 및 입력 불변(time- and input-invariant)이어야 한다. 우리는 이를 convolution 대신 scan으로 모델을 recurrent하게 계산하는 hardware-aware algorithm으로 극복한다. 이 알고리즘은 GPU 메모리 계층의 다른 레벨 간의 IO 접근을 피하기 위해 확장된 상태를 구체화하지 않는다. 결과적으로 구현된 방식은 이론적으로 (모든 convolution 기반 SSM에 대해 pseudo-linear인 것과 비교하여 시퀀스 길이에 대해 선형적으로 스케일링) 그리고 현대 하드웨어에서 (A100 GPU에서 최대 3배 빠름) 기존 방법보다 빠르다.
Architecture. 우리는 기존 SSM 아키텍처 (Dao, Fu, Saab, et al. 2023)의 설계와 Transformer의 MLP 블록을 단일 블록으로 결합하여 기존의 심층 시퀀스 모델 아키텍처를 단순화한다. 이는 **selective state space를 통합한 간단하고 균일한 아키텍처 설계 (Mamba)**로 이어진다. Selective SSM, 그리고 더 나아가 Mamba 아키텍처는 일반적인 Foundation Model의 backbone으로 적합한 핵심 속성을 가진 완전한 recurrent model이다. (i) 높은 품질: **선택성(selectivity)**은 언어 및 유전체학과 같은 밀도 높은 양식에서 강력한 성능을 가져온다. (ii) 빠른 학습 및 추론: 학습 중 계산 및 메모리는 시퀀스 길이에 대해 선형적으로 스케일링하며, 추론 중 모델을 autoregressive하게 unroll하는 것은 이전 요소의 캐시를 필요로 하지 않으므로 단계당 일정한 시간만 필요하다. (iii) 긴 context: 품질과 효율성이 결합되어 최대 1M 시퀀스 길이의 실제 데이터에서 성능 향상을 가져온다. 우리는 Mamba의 잠재력을 일반적인 시퀀스 FM backbone으로서 경험적으로 검증하며, 사전학습 품질 및 도메인별 task 성능 모두에서 여러 유형의 양식 및 설정에 대해 검증한다:
- Synthetics. 대규모 언어 모델의 핵심으로 제안된 copying 및 induction heads와 같은 중요한 합성 task에서 Mamba는 이를 쉽게 해결할 뿐만 아니라 무기한으로 긴 시퀀스 (>1M 토큰)에 대한 솔루션을 외삽할 수 있다.
- Audio and Genomics. Mamba는 오디오 파형 및 DNA 시퀀스 모델링에서 SaShiMi, Hyena, Transformer와 같은 기존 state-of-the-art 모델을 능가하며, 사전학습 품질 및 다운스트림 metric (예: 어려운 음성 생성 데이터셋에서 FID를 절반 이상 감소) 모두에서 우수한 성능을 보인다. 두 설정 모두에서 백만 길이 시퀀스까지 더 긴 context에서 성능이 향상된다.
- Language Modeling. Mamba는 사전학습 perplexity 및 다운스트림 평가 모두에서 Transformer 수준의 성능을 진정으로 달성한 최초의 선형 시간 시퀀스 모델이다. 최대 1B 파라미터까지의 스케일링 법칙을 통해, Mamba는 LLaMa (Touvron et al. 2023)에 기반한 매우 강력한 최신 Transformer 학습 레시피를 포함하여 광범위한 baseline의 성능을 능가함을 보여준다. 우리의 Mamba language model은 유사한 크기의 Transformer에 비해 5배의 생성 처리량을 가지며, Mamba-3B의 품질은 두 배 크기의 Transformer와 일치한다 (예: Pythia-3B에 비해 일반 상식 추론에서 평균 4점 더 높고 Pythia-7B도 능가).
모델 코드 및 사전학습된 체크포인트는 https://github.com/state-spaces/mamba에서 오픈 소스로 공개되어 있다.
2 State Space Models
**Structured state space sequence model (S4)**은 RNN, CNN, 그리고 고전적인 state space model과 폭넓게 연관된, 딥러닝을 위한 최신 시퀀스 모델 클래스이다. 이 모델들은 특정 연속 시스템 (1)에서 영감을 받았다.
Selective State Space Model
with Hardware-aware State Expansion
 Figure 1: (개요.) Structured SSM은 입력 의 각 채널(예: )을 더 높은 차원의 잠재 상태 (예: )를 통해 출력 로 독립적으로 매핑한다. 기존 SSM은 **시간 불변성(time-invariance)**을 요구하는 영리한 대체 계산 경로를 통해 이 큰 유효 상태(, 배치 크기 및 시퀀스 길이 을 곱한 값)를 구체화하는 것을 피한다: 파라미터는 시간에 걸쳐 일정하다. 우리의 **선택 메커니즘(selection mechanism)**은 입력 의존적인 동역학을 다시 추가하며, 이는 확장된 상태를 GPU 메모리 계층의 더 효율적인 수준에서만 구체화하도록 하는 **하드웨어 인식 알고리즘(hardware-aware algorithm)**을 필요로 한다.
Figure 1: (개요.) Structured SSM은 입력 의 각 채널(예: )을 더 높은 차원의 잠재 상태 (예: )를 통해 출력 로 독립적으로 매핑한다. 기존 SSM은 **시간 불변성(time-invariance)**을 요구하는 영리한 대체 계산 경로를 통해 이 큰 유효 상태(, 배치 크기 및 시퀀스 길이 을 곱한 값)를 구체화하는 것을 피한다: 파라미터는 시간에 걸쳐 일정하다. 우리의 **선택 메커니즘(selection mechanism)**은 입력 의존적인 동역학을 다시 추가하며, 이는 확장된 상태를 GPU 메모리 계층의 더 효율적인 수준에서만 구체화하도록 하는 **하드웨어 인식 알고리즘(hardware-aware algorithm)**을 필요로 한다.
1차원 함수 또는 시퀀스 를 암묵적인 잠재 상태 를 통해 변환한다. 구체적으로, S4 모델은 네 가지 파라미터 로 정의되며, 이는 두 단계로 시퀀스-투-시퀀스 변환을 정의한다.
이산화(Discretization). 첫 번째 단계는 "연속 파라미터" 를 고정된 공식 및 를 통해 "이산 파라미터" 로 변환한다. 여기서 쌍 를 **이산화 규칙(discretization rule)**이라고 한다. 방정식 (4)에 정의된 **영차 홀드(zero-order hold, ZOH)**와 같은 다양한 규칙을 사용할 수 있다.
이산화는 **연속 시간 시스템(continuous-time systems)**과 깊은 관련이 있으며, 이를 통해 해상도 불변성(resolution invariance)(Nguyen, Goel, et al. 2022)과 같은 추가 속성을 부여하고 모델이 적절하게 정규화되도록 자동으로 보장할 수 있다(Gu, Johnson, Timalsina, et al. 2023; Orvieto et al. 2023). 또한 Section 3.5에서 다시 다룰 RNN의 **게이팅 메커니즘(gating mechanisms)**과도 관련이 있다(Gu, Gulcehre, et al. 2020; Tallec and Ollivier 2018). 그러나 기계적인 관점에서 이산화는 단순히 SSM의 **순방향 전달(forward pass)**에서 계산 그래프의 첫 번째 단계로 볼 수 있다. 다른 종류의 SSM은 이산화 단계를 건너뛰고 를 직접 파라미터화할 수 있으며(Zhang et al. 2023), 이는 추론하기 더 쉬울 수 있다.
계산(Computation). 파라미터가 로 변환된 후, 모델은 선형 재귀(linear recurrence) (2) 또는 전역 컨볼루션(global convolution) (3)의 두 가지 방식으로 계산될 수 있다.
일반적으로 모델은 효율적인 병렬 학습(전체 입력 시퀀스를 미리 볼 수 있는 경우)을 위해 컨볼루션 모드(convolutional mode) (3)를 사용하고, 효율적인 자기회귀 추론(autoregressive inference)(입력이 한 번에 한 타임스텝씩 보이는 경우)을 위해 재귀 모드(recurrent mode) (2)로 전환된다.
선형 시간 불변성(Linear Time Invariance, LTI). 방정식 (1)부터 (3)의 중요한 속성은 모델의 동역학이 시간에 걸쳐 일정하다는 것이다. 즉, 와 결과적으로 도 모든 타임스텝에 대해 고정된다. 이 속성을 **선형 시간 불변성(LTI)**이라고 하며, 이는 재귀 및 컨볼루션과 깊이 관련되어 있다. 비공식적으로, 우리는 LTI SSM을 모든 선형 재귀 (2a) 또는 컨볼루션 (3b)와 동등하다고 생각하며, LTI를 이러한 모델 클래스에 대한 포괄적인 용어로 사용한다.
지금까지 모든 structured SSM은 Section 3.3에서 논의된 근본적인 효율성 제약으로 인해 LTI(예: 컨볼루션으로 계산됨)였다. 그러나 이 연구의 핵심 통찰력은 LTI 모델이 특정 유형의 데이터를 모델링하는 데 근본적인 한계를 가지고 있으며, 우리의 기술적 기여는 효율성 병목 현상을 극복하면서 LTI 제약을 제거하는 것을 포함한다.
구조 및 차원(Structure and Dimensions). 마지막으로, structured SSM은 효율적인 계산을 위해 행렬에 구조를 부과해야 하므로 그렇게 명명되었다는 점에 주목한다. 가장 인기 있는 구조 형태는 **대각선(diagonal)**이다(Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Smith, Warrington, and Linderman 2023). 우리도 이 구조를 사용한다. 이 경우, 행렬은 모두 개의 숫자로 표현될 수 있다. 배치 크기 와 길이 을 가진 채널의 입력 시퀀스 에 대해 작동하기 위해, SSM은 각 채널에 독립적으로 적용된다. 이 경우, 총 은닉 상태는 입력당 차원을 가지며, 시퀀스 길이에 걸쳐 이를 계산하는 데 시간과 메모리가 필요하다. 이것이 Section 3.3에서 다루는 근본적인 효율성 병목 현상의 근원이다.
일반 상태 공간 모델(General State Space Models). **상태 공간 모델(state space model)**이라는 용어는 잠재 상태를 가진 모든 재귀 프로세스의 개념을 단순히 나타내는 매우 넓은 의미를 가진다. 이는 마르코프 결정 프로세스(Markov decision processes, MDP)(강화 학습 (Hafner et al. 2020)), 동적 인과 모델링(dynamic causal modeling, DCM)(계산 신경과학 (Friston, Harrison, and Penny 2003)), 칼만 필터(Kalman filters)(제어 (Kalman 1960)), 은닉 마르코프 모델(hidden Markov models, HMM) 및 선형 동적 시스템(linear dynamical systems, LDS)(머신러닝), 그리고 전반적인 재귀(때로는 컨볼루션) 모델(딥러닝)을 포함하여 다양한 분야에서 많은 이질적인 개념을 지칭하는 데 사용되어 왔다.
이 논문 전체에서 우리는 "SSM"이라는 용어를 structured SSM 또는 S4 모델 클래스(Gu, Goel, and Ré 2022; Gu, Gupta, et al. 2022; Gupta, Gu, and Berant 2022; Hasani et al. 2023; Ma et al. 2023; Smith, Warrington, and Linderman 2023)만을 지칭하는 데 사용하며, 이 용어들을 상호 교환적으로 사용한다. 편의를 위해 우리는 선형 재귀 또는 전역 컨볼루션 관점에 초점을 맞춘 모델과 같은 이러한 모델의 파생 모델도 포함할 수 있으며(Y. Li et al. 2023; Orvieto et al. 2023; Poli et al. 2023), 필요한 경우 미묘한 차이를 명확히 한다.
SSM 아키텍처(SSM Architectures). SSM은 **독립적인 시퀀스 변환(standalone sequence transformations)**이며, **종단 간 신경망 아키텍처(end-to-end neural network architectures)**에 통합될 수 있다. (우리는 때때로 SSM 아키텍처를 SSNN이라고도 부르는데, 이는 CNN이 선형 컨볼루션 레이어에 대한 관계와 유사하게 SSM 레이어에 대한 관계이다.) 우리는 가장 잘 알려진 SSM 아키텍처 중 일부를 논의할 것이며, 이들 중 다수는 우리의 주요 **기준선(baselines)**으로도 사용될 것이다.
- Linear attention(Katharopoulos et al. 2020)은 **퇴화된 선형 SSM(degenerate linear SSM)**으로 볼 수 있는 재귀를 포함하는 self-attention의 근사치이다.
- H3(Dao, Fu, Saab, et al. 2023)는 이 재귀를 S4를 사용하도록 일반화했다. 이는 두 개의 게이트 연결(gated connections) 사이에 SSM이 끼워진 아키텍처로 볼 수 있다(Figure 3). H3는 또한 주 SSM 레이어 전에 표준 **로컬 컨볼루션(local convolution)**을 삽입하는데, 이를 shift-SSM으로 구성한다.
- Hyena(Poli et al. 2023)는 H3와 동일한 아키텍처를 사용하지만, S4 레이어를 MLP-parameterized global convolution(Romero et al. 2021)으로 대체한다.
- RetNet(Y. Sun et al. 2023)은 아키텍처에 추가 게이트를 추가하고 더 간단한 SSM을 사용하여, 컨볼루션 대신 **multi-head attention(MHA)**의 변형을 사용하여 대체 병렬 계산 경로를 허용한다.
- RWKV(B. Peng et al. 2023)는 또 다른 linear attention 근사치인 attention-free Transformer(S. Zhai et al. 2021)를 기반으로 한 언어 모델링을 위해 설계된 최신 RNN이다. 주요 "WKV" 메커니즘은 LTI 재귀를 포함하며 두 SSM의 비율로 볼 수 있다.
다른 밀접하게 관련된 SSM 및 아키텍처는 확장된 관련 연구(Appendix B)에서 더 자세히 논의된다. 특히 S5(Smith, Warrington, and Linderman 2023), QRNN(Bradbury et al. 2016), SRU(Lei et al. 2017)를 강조하며, 이들을 우리의 핵심 selective SSM과 가장 밀접하게 관련된 방법으로 간주한다.
3 Selective State Space Models
우리는 먼저 합성 task로부터 얻은 직관을 사용하여 **선택 메커니즘(selection mechanism)**의 필요성을 설명하고(Section 3.1), 이 메커니즘을 **state space model (SSM)**에 통합하는 방법을 설명한다(Section 3.2). 그 결과로 얻어지는 **시간 가변 SSM(time-varying SSM)**은 convolution을 사용할 수 없으므로, 이를 효율적으로 계산하는 기술적인 과제가 발생한다. 우리는 현대 하드웨어의 메모리 계층 구조를 활용하는 하드웨어 인식 알고리즘으로 이 문제를 해결한다(Section 3.3). 이어서 attention이나 MLP 블록조차 없는 간단한 SSM 아키텍처를 설명한다(Section 3.4). 마지막으로, 선택 메커니즘의 몇 가지 추가적인 속성에 대해 논의한다(Section 3.5).
3.1 Motivation: Selection as a Means of Compression
우리는 시퀀스 모델링의 근본적인 문제가 context를 더 작은 state로 압축하는 것이라고 주장한다. 실제로, 인기 있는 시퀀스 모델들의 trade-off를 이러한 관점에서 볼 수 있다. 예를 들어, attention은 context를 전혀 압축하지 않기 때문에 효과적이면서도 비효율적이다. 이는 autoregressive inference가 전체 context(즉, KV cache)를 명시적으로 저장해야 하며, 이로 인해 Transformer의 느린 선형 시간 추론(linear-time inference)과 이차 시간 학습(quadratic-time training)이 직접적으로 발생한다는 사실에서 알 수 있다. 반면에 recurrent model은 유한한 state를 가지므로 효율적이며, 이는 상수 시간 추론(constant-time inference)과 선형 시간 학습(linear-time training)을 의미한다. 그러나 이들의 효과는 state가 context를 얼마나 잘 압축했는지에 따라 제한된다.
이 원리를 이해하기 위해, 우리는 두 가지 합성 task 예시에 초점을 맞춘다 (Figure 2).
- Selective Copying task는 인기 있는 Copying task (Arjovsky, Shah, and Bengio 2016)를 변형하여 기억해야 할 토큰의 위치를 다양하게 변경한다. 이 task는 관련 토큰(색깔 있는)을 기억하고 관련 없는 토큰(흰색)을 걸러내기 위해 내용 인식(content-aware) 추론을 요구한다.
- Induction Heads task는 LLM의 in-context learning 능력 대부분을 설명하는 것으로 가설화된 잘 알려진 메커니즘이다 (Olsson et al. 2022). 이 task는 적절한 context에서 올바른 출력을 언제 생성해야 하는지 알기 위해 context 인식(context-aware) 추론을 요구한다 (검은색).
이러한 task들은 LTI 모델의 실패 모드를 보여준다. recurrent 관점에서 보면, 이들의 상수적인 동역학(constant dynamics) (예: (2)의 () 전이)은 context에서 올바른 정보를 선택하거나, 입력에 따라 시퀀스를 따라 전달되는 hidden state에 영향을 미치지 못한다. convolutional 관점에서 보면, global convolution은 시간 인식(time-awareness)만 요구하는 vanilla Copying task를 해결할 수 있지만 (Romero et al. 2021), 내용 인식(content-awareness) 부족으로 인해 Selective Copying task에서는 어려움을 겪는 것으로 알려져 있다 (Figure 2). 더 구체적으로, 입력-출력 간의 간격이 가변적이어서 정적 convolution kernel로는 모델링할 수 없다.
요약하자면, 시퀀스 모델의 효율성 대 효과성 trade-off는 state를 얼마나 잘 압축하는지에 따라 특징지어진다: 효율적인 모델은 작은 state를 가져야 하고, 효과적인 모델은 context로부터 필요한 모든 정보를 포함하는 state를 가져야 한다. 이에 따라, 우리는 시퀀스 모델을 구축하는 근본적인 원리가 선택성(selectivity), 즉 순차적인 state로 입력을 집중하거나 걸러내는 context 인식 능력이라고 제안한다. 특히, 선택 메커니즘은 정보가 시퀀스 차원을 따라 어떻게 전파되거나 상호작용하는지를 제어한다 (자세한 논의는 Section 3.5 참조).
3.2 Improving SSMs with Selection
모델에 선택 메커니즘을 통합하는 한 가지 방법은 시퀀스를 따라 상호작용에 영향을 미치는 파라미터(예: RNN의 recurrent dynamics 또는 CNN의 convolution kernel)가 입력에 의존하도록 하는 것이다.
Algorithm 1과 Algorithm 2는 우리가 사용하는 주요 선택 메커니즘을 보여준다. 주요 차이점은 단순히 여러 파라미터 를 입력의 함수로 만들고, 그에 따른 텐서 형태의 변화를 적용하는 것이다. 특히, 이 파라미터들이 이제 길이 차원 을 가지게 되어, 모델이 시간 불변(time-invariant)에서 시간 가변(time-varying)으로 변경되었음을 강조한다. (형태 주석은 Section 2에서 설명되었다.) 이는 convolution (3)과의 등가성을 잃게 되며, 효율성에 대한 함의는 다음에서 논의된다.
우리는 구체적으로 , , , 그리고 softplus를 선택하며, 여기서 는 차원 로의 parameterized projection이다. 와 의 선택은 Section 3.5에서 설명된 RNN gating mechanism과의 연관성 때문이다.
 Figure 2:
(왼쪽) Copying task의 표준 버전은 입력과 출력 요소 간의 간격이 일정하며, 선형 recurrence 및 global convolution과 같은 time-invariant 모델로 쉽게 해결된다.
(오른쪽 상단) Selective Copying task는 입력 사이에 무작위 간격이 있으며, 내용에 따라 입력을 선택적으로 기억하거나 무시할 수 있는 time-varying 모델을 필요로 한다.
(오른쪽 하단) Induction Heads task는 LLM의 핵심 능력인 context 기반으로 답변을 검색해야 하는 연관 기억(associative recall)의 예시이다.
Figure 2:
(왼쪽) Copying task의 표준 버전은 입력과 출력 요소 간의 간격이 일정하며, 선형 recurrence 및 global convolution과 같은 time-invariant 모델로 쉽게 해결된다.
(오른쪽 상단) Selective Copying task는 입력 사이에 무작위 간격이 있으며, 내용에 따라 입력을 선택적으로 기억하거나 무시할 수 있는 time-varying 모델을 필요로 한다.
(오른쪽 하단) Induction Heads task는 LLM의 핵심 능력인 context 기반으로 답변을 검색해야 하는 연관 기억(associative recall)의 예시이다.
Algorithm 1 SSM (S4)
Input: \(x:(\mathrm{B}, \mathrm{L}, \mathrm{D})\)
Output: \(y:(\mathrm{B}, \mathrm{L}, \mathrm{D})\)
\(\boldsymbol{A}:(\mathrm{D}, \mathrm{N}) \leftarrow\) Parameter
\(\triangleright\) Represents structured \(N \times N\) matrix
\(\boldsymbol{B}:(\mathrm{D}, \mathrm{N}) \leftarrow\) Parameter
\(C:(\mathrm{D}, \mathrm{N}) \leftarrow\) Parameter
\(\Delta:(\mathrm{D}) \leftarrow \tau_{\Delta}\) (Parameter)
\(\overline{\boldsymbol{A}}, \overline{\boldsymbol{B}}:(\mathrm{D}, \mathrm{N}) \leftarrow \operatorname{discretize}(\Delta, \boldsymbol{A}, \boldsymbol{B})\)
\(y \leftarrow \operatorname{SSM}(\overline{\boldsymbol{A}}, \overline{\boldsymbol{B}}, C)(x)\)
\(\triangleright\) Time-invariant: recurrence or convolution
return \(y\)
Algorithm 2 SSM + Selection (S6)
Input: \(x:(\mathrm{B}, \mathrm{L}, \mathrm{D})\)
Output: \(y:(\mathrm{B}, \mathrm{L}, \mathrm{D})\)
\(A:(\mathrm{D}, \mathrm{N}) \leftarrow\) Parameter
\(\triangleright\) Represents structured \(N \times N\) matrix
\(\boldsymbol{B}:(\mathrm{B}, \mathrm{L}, \mathrm{N}) \leftarrow s_{B}(x)\)
\(C:(\mathrm{B}, \mathrm{L}, \mathrm{N}) \leftarrow s_{C}(x)\)
\(\underline{\Delta}:(\mathrm{B}, \mathrm{L}, \mathrm{D}) \leftarrow \tau_{\Delta}\left(\right.\) Parameter \(\left.+s_{\Delta}(x)\right)\)
\(\overline{\boldsymbol{A}}, \overline{\boldsymbol{B}}:(\mathrm{B}, \mathrm{L}, \mathrm{D}, \mathrm{N}) \leftarrow \operatorname{discretize}(\Delta, \boldsymbol{A}, \boldsymbol{B})\)
\(y \leftarrow \operatorname{SSM}(\overline{\boldsymbol{A}}, \overline{\boldsymbol{B}}, C)(x)\)
- Time-varying: recurrence (scan) only
return \(y\)
3.3 Efficient Implementation of Selective SSMs
컨볼루션(Krizhevsky, Sutskever, and Hinton 2012) 및 attention(Bahdanau, Cho, and Bengio 2015; Vaswani et al. 2017)과 같은 하드웨어 친화적인 primitive는 널리 사용되고 있다. 본 연구에서는 selective SSM 또한 최신 하드웨어(GPU)에서 효율적으로 동작하도록 만드는 것을 목표로 한다.
선택 메커니즘은 매우 자연스러우며, 초기 연구에서는 recurrent SSM에서 가 시간에 따라 변하도록 하는 것과 같은 선택의 특수한 경우를 통합하려고 시도했다(Gu, Dao, et al. 2020). 그러나 앞서 언급했듯이, SSM 사용의 핵심적인 한계는 계산 효율성이었고, 이것이 S4 및 모든 파생 모델들이 LTI(non-selective) 모델, 가장 일반적으로 global convolution 형태를 사용한 이유였다.
3.3.1 Motivation of Prior Models
우리는 먼저 이러한 동기를 다시 살펴보고, 기존 방법의 한계를 극복하기 위한 접근 방식을 개괄적으로 설명한다.
- 높은 수준에서, SSM과 같은 recurrent model은 항상 표현력(expressivity)과 속도 사이의 trade-off를 가진다. Section 3.1에서 논의했듯이, 더 큰 hidden state dimension을 가진 모델은 더 효과적이지만 더 느려야 한다. 따라서 우리는 속도 및 메모리 비용을 지불하지 않고 hidden state dimension을 최대화하고자 한다.
- recurrent mode는 convolution mode보다 더 유연하다는 점에 주목해야 한다. 후자(3)는 전자(2)를 확장하여 파생되었기 때문이다 (Gu, Goel, and Ré 2022; Gu, Johnson, Goel, et al. 2021). 그러나 이는 (B, L, D, N) 형태의 latent state 를 계산하고 구체화(materializing)해야 하는데, 이는 (B, L, D) 형태의 입력 및 출력 보다 훨씬 크다 (SSM state dimension인 N배만큼). 따라서 state 계산을 우회하고 (B, L, D) 크기의 convolution kernel (3a)만 구체화할 수 있는 더 효율적인 convolution mode가 도입되었다.
- 기존 LTI state space model은 recurrent-convolutional 이중 형태를 활용하여 효율성 저하 없이 유효 state dimension을 N배(약 10-100배) 증가시켰으며, 이는 전통적인 RNN보다 훨씬 크다.
3.3.2 Overview of Selective Scan: Hardware-Aware State Expansion
선택 메커니즘은 LTI 모델의 한계를 극복하도록 설계되었으며, 동시에 우리는 SSM의 연산 문제를 재검토해야 한다. 우리는 이를 **커널 퓨전(kernel fusion), 병렬 스캔(parallel scan), 재연산(recomputation)**이라는 세 가지 고전적인 기술로 해결한다. 우리는 두 가지 주요 관찰을 통해 이를 설명한다:
- 순환(recurrent) 연산은 FLOPs를 사용하는 반면, 합성곱(convolutional) 연산은 FLOPs를 사용하며, 전자가 더 낮은 상수 계수를 가진다. 따라서 긴 시퀀스와 너무 크지 않은 상태 차원 에 대해서는 순환 모드가 실제로 더 적은 FLOPs를 사용할 수 있다.
- 두 가지 주요 과제는 순환의 순차적 특성과 많은 메모리 사용량이다. 후자를 해결하기 위해, 합성곱 모드와 마찬가지로, 전체 상태 를 실제로 구체화하지 않으려고 시도할 수 있다.
주요 아이디어는 현대 가속기(GPU)의 특성을 활용하여 메모리 계층 구조의 더 효율적인 수준에서만 상태 를 구체화하는 것이다. 특히, 대부분의 연산(행렬 곱셈 제외)은 메모리 대역폭에 의해 제한된다 (Dao, Fu, Ermon, et al. 2022; Ivanov et al. 2021; Williams, Waterman, and Patterson 2009). 여기에는 우리의 스캔(scan) 연산도 포함되며, 우리는 커널 퓨전(kernel fusion)을 사용하여 메모리 IO 양을 줄여 표준 구현에 비해 상당한 속도 향상을 이끌어냈다.
구체적으로, GPU HBM(high-bandwidth memory)에 크기 의 스캔 입력()을 준비하는 대신, SSM 파라미터()를 느린 HBM에서 빠른 SRAM으로 직접 로드하고, SRAM에서 이산화(discretization) 및 순환(recurrence)을 수행한 다음, 크기 의 최종 출력을 다시 HBM으로 기록한다.
순차적인 순환을 피하기 위해, 우리는 선형적이지 않음에도 불구하고 작업 효율적인 병렬 스캔 알고리즘(work-efficient parallel scan algorithm)으로 여전히 병렬화될 수 있음을 관찰했다 (Blelloch 1990; Martin and Cundy 2018; Smith, Warrington, and Linderman 2023).
마지막으로, 역전파에 필요한 중간 상태를 저장하는 것도 피해야 한다. 우리는 재연산(recomputation)이라는 고전적인 기술을 신중하게 적용하여 메모리 요구 사항을 줄였다: 중간 상태는 저장되지 않고, 입력이 HBM에서 SRAM으로 로드될 때 역방향 패스(backward pass)에서 재연산된다. 결과적으로, 퓨전된 선택적 스캔(fused selective scan) 레이어는 FlashAttention이 적용된 최적화된 Transformer 구현과 동일한 메모리 요구 사항을 가진다.
퓨전된 커널 및 재연산에 대한 자세한 내용은 Appendix D에 있다. 전체 Selective SSM 레이어 및 알고리즘은 Figure 1에 설명되어 있다.
3.4 A Simplified SSM Architecture
구조화된 SSM과 마찬가지로, selective SSM은 신경망에 유연하게 통합될 수 있는 독립적인 시퀀스 변환이다. H3 아키텍처는 가장 잘 알려진 SSM 아키텍처(Section 2)의 기반이며, 일반적으로 linear attention에서 영감을 받은 블록과 MLP(multi-layer perceptron) 블록이 교차(interleave)된 형태로 구성된다. 우리는 이 두 구성 요소를 하나로 결합하여 동질적으로 쌓아 올림으로써(Figure 3) 이 아키텍처를 단순화한다. 이는 attention에 대해 유사한 작업을 수행했던 GAU(gated attention unit) (Hua et al. 2022)에서 영감을 받았다.
이 아키텍처는 모델 차원 를 제어 가능한 확장 계수 만큼 확장하는 것을 포함한다. 각 블록에서 대부분의 파라미터()는 **선형 투영(linear projection)**에 있으며 (입력 투영에 , 출력 투영에 ), 내부 SSM은 더 적은 파라미터를 가진다. SSM 파라미터( 에 대한 투영 및 행렬 )의 수는 이에 비해 훨씬 작다. 우리는 이 블록을 표준 정규화(normalization) 및 잔차 연결(residual connection)과 교차하여 반복함으로써 Mamba 아키텍처를 형성한다. 우리는 실험에서 항상 로 고정하고, Transformer의 교차된 MHA(multi-head attention) 및 MLP 블록의 파라미터에 맞추기 위해 두 개의 블록 스택을 사용한다. 우리는 SiLU / Swish 활성화 함수 (Hendrycks and Gimpel 2016; Ramachandran, Zoph, and Quoc V Le 2017)를 사용하는데, 이는 Gated MLP가 인기 있는 "SwiGLU" 변형 (Chowdhery et al. 2023; Dauphin et al. 2017; Shazeer 2020; Touvron et al. 2023)이 되도록 동기 부여된 것이다. 마지막으로, 우리는 RetNet이 유사한 위치에 정규화 레이어를 사용한 것 (Y. Sun et al. 2023)에서 영감을 받아 선택적 정규화 레이어(우리는 LayerNorm (J. L. Ba, Kiros, and Hinton 2016)을 선택)를 추가적으로 사용한다.
3.5 Properties of Selection Mechanisms
선택 메커니즘은 더 전통적인 RNN이나 CNN, 다른 파라미터(예: Algorithm 2의 ), 또는 다른 변환 등 다양한 방식으로 적용될 수 있는 더 넓은 개념이다.
 Figure 3: (아키텍처.) 우리의 간소화된 블록 설계는 대부분의 SSM 아키텍처의 기반이 되는 H3 블록과 현대 신경망의 보편적인 MLP 블록을 결합한다. 이 두 블록을 교차(interleave)하는 대신, 우리는 Mamba 블록을 균일하게 반복한다. H3 블록과 비교하여 Mamba는 첫 번째 곱셈 게이트를 활성화 함수로 대체한다. MLP 블록과 비교하여 Mamba는 주 브랜치에 SSM을 추가한다. 에는 SiLU / Swish 활성화 함수를 사용한다 (Hendrycks and Gimpel 2016; Ramachandran, Zoph, and Quoc V Le 2017).
Figure 3: (아키텍처.) 우리의 간소화된 블록 설계는 대부분의 SSM 아키텍처의 기반이 되는 H3 블록과 현대 신경망의 보편적인 MLP 블록을 결합한다. 이 두 블록을 교차(interleave)하는 대신, 우리는 Mamba 블록을 균일하게 반복한다. H3 블록과 비교하여 Mamba는 첫 번째 곱셈 게이트를 활성화 함수로 대체한다. MLP 블록과 비교하여 Mamba는 주 브랜치에 SSM을 추가한다. 에는 SiLU / Swish 활성화 함수를 사용한다 (Hendrycks and Gimpel 2016; Ramachandran, Zoph, and Quoc V Le 2017).
3.5.1 Connection to Gating Mechanisms
우리는 가장 중요한 연결점을 강조한다: RNN의 고전적인 gating mechanism은 SSM을 위한 우리의 선택 메커니즘의 한 예시이다. RNN gating과 연속 시간 시스템의 이산화(discretization) 사이의 연결은 잘 확립되어 있다 (Funahashi and Nakamura 1993; Tallec and Ollivier 2018). 사실, Theorem 1은 Gu, Johnson, Goel, et al. (2021, Lemma 3.1)의 개선된 버전으로, ZOH 이산화 및 입력 의존적인 gate로 일반화된다 (증명은 Appendix C). 더 넓게 보면, SSM에서 는 RNN gating mechanism의 일반화된 역할을 한다고 볼 수 있다. 이전 연구와 마찬가지로, 우리는 SSM의 이산화가 휴리스틱한 gating mechanism의 원칙적인 기반이라는 관점을 채택한다.
Theorem 1. , 그리고 softplus일 때, **선택적 SSM recurrence (Algorithm 2)**는 다음 형태를 취한다:
Section 3.2에서 언급했듯이, 에 대한 우리의 특정 선택은 이 연결에서 비롯된다. 특히, 주어진 입력 가 (합성 task에서 필요한 것처럼) 완전히 무시되어야 한다면, 모든 채널이 이를 무시해야 하므로, 우리는 와 반복/브로드캐스팅하기 전에 입력을 1차원으로 투영한다.
3.5.2 Interpretation of Selection Mechanisms
우리는 선택성(selectivity)의 세 가지 특정 메커니즘적 효과에 대해 자세히 설명한다.
가변 간격 (Variable Spacing). 선택성은 관심 있는 입력 사이에 발생할 수 있는 관련 없는 노이즈 토큰을 필터링할 수 있게 한다. 이는 Selective Copying task에서 예시되지만, 특히 이산 데이터(discrete data)의 경우 일반적인 데이터 양식에서 보편적으로 발생한다. 예를 들어 "음"과 같은 언어 필러(language filler)의 존재가 그렇다. 이 속성은 모델이 특정 입력 를 기계적으로 필터링할 수 있기 때문에 발생한다. 예를 들어 gated RNN의 경우 (Theorem 1) 일 때 그렇다.
컨텍스트 필터링 (Filtering Context). 많은 시퀀스 모델이 더 긴 컨텍스트에서 성능이 향상되지 않는다는 것이 경험적으로 관찰되었다 (F. Shi et al. 2023). 이는 더 많은 컨텍스트가 엄밀히 더 나은 성능으로 이어져야 한다는 원칙에도 불구하고 그렇다. 이에 대한 설명은 많은 시퀀스 모델이 필요할 때 관련 없는 컨텍스트를 효과적으로 무시할 수 없기 때문이며, 직관적인 예시로는 global convolution (및 일반적인 LTI 모델)이 있다. 반면에 선택적 모델은 언제든지 상태를 재설정하여 불필요한 이력을 제거할 수 있으므로, 원칙적으로 컨텍스트 길이에 따라 성능이 단조롭게 향상된다 (예: Section 4.3.2).
경계 재설정 (Boundary Resetting). 여러 독립적인 시퀀스가 함께 연결되는 설정에서, Transformer는 특정 attention mask를 인스턴스화하여 시퀀스들을 분리할 수 있는 반면, LTI 모델은 시퀀스들 사이에 정보가 새어 나간다. Selective SSMs 또한 경계에서 상태를 재설정할 수 있다 (예: , 또는 Theorem 1에서 일 때). 이러한 설정은 인위적으로 발생할 수 있거나 (예: 하드웨어 활용도를 높이기 위해 문서를 함께 묶는 경우) 자연적으로 발생할 수 있다 (예: 강화 학습의 에피소드 경계 (Lu et al. 2023)). 또한, 우리는 각 선택적 파라미터의 효과에 대해 자세히 설명한다.
의 해석 (Interpretation of ). 일반적으로 는 현재 입력 에 얼마나 집중하거나 무시할 것인지 사이의 균형을 제어한다. 이는 RNN gate를 일반화한다 (예: Theorem 1의 ): 기계적으로, 큰 는 상태 를 재설정하고 현재 입력 에 집중하는 반면, 작은 는 상태를 유지하고 현재 입력을 무시한다. SSMs (1)-(2)는 시점 에 의해 이산화된 연속 시스템으로 해석될 수 있으며, 이 맥락에서 직관은 큰 가 시스템이 현재 입력에 더 오래 집중하는 것을 나타내고 (따라서 이를 "선택"하고 현재 상태를 잊어버림), 작은 는 무시되는 일시적인 입력을 나타낸다는 것이다.
의 해석 (Interpretation of ). 파라미터도 선택적일 수 있지만, 궁극적으로는 이산화 (4)를 통해 를 통해 와의 상호작용을 통해서만 모델에 영향을 미친다는 점을 언급한다. 따라서 에서의 선택성은 ()에서의 선택성을 보장하기에 충분하며, 성능 향상의 주요 원천이다. 우리는 외에 (또는 대신) 를 선택적으로 만드는 것이 유사한 성능을 가질 것이라고 가정하며, 단순화를 위해 이를 제외한다.
와 의 해석 (Interpretation of and ). Section 3.1에서 논의했듯이, 선택성의 가장 중요한 속성은 관련 없는 정보를 필터링하여 시퀀스 모델의 컨텍스트를 효율적인 상태로 압축할 수 있도록 하는 것이다. SSM에서 와 를 선택적으로 수정하는 것은 입력 를 상태 로 허용할지, 또는 상태를 출력 로 허용할지에 대한 더 세밀한 제어를 가능하게 한다. 이는 모델이 각각 내용(입력)과 컨텍스트(hidden states)에 따라 recurrent dynamics를 조절할 수 있도록 허용하는 것으로 해석될 수 있다.
3.6 Additional Model Details
실수(Real) vs. 복소수(Complex)
대부분의 기존 SSM은 state 에 **복소수(complex numbers)**를 사용하는데, 이는 많은 지각(perceptual) 양식(modality) task에서 강력한 성능을 위해 필수적이다 (Gu, Goel, and Ré 2022). 그러나 완전히 실수(real-valued) SSM도 일부 설정에서는 잘 작동하며, 심지어 더 나은 성능을 보이는 경우도 경험적으로 관찰되었다 (Ma et al. 2023). 우리는 기본적으로 실수 값을 사용하며, 이는 우리의 task 중 하나를 제외하고는 모두 잘 작동한다. 우리는 복소수-실수 간의 trade-off가 데이터 양식의 연속-이산 스펙트럼과 관련이 있다고 가정한다. 즉, 복소수는 연속적인 양식(예: 오디오, 비디오)에 유용하지만, 이산적인 양식(예: 텍스트, DNA)에는 그렇지 않다는 것이다.
초기화(Initialization)
대부분의 기존 SSM은 특히 복소수 값의 경우 특별한 초기화를 제안하며, 이는 데이터가 적은(low-data) 환경과 같은 여러 설정에서 도움이 될 수 있다. 복소수 경우의 기본 초기화는 S4D-Lin이고, 실수 경우의 기본 초기화는 S4D-Real이다 (Gu, Gupta, et al. 2022). 이는 HIPPO 이론 (Gu, Dao, et al. 2020)에 기반한다. 이들은 의 번째 요소를 각각 와 로 정의한다. 그러나 우리는 특히 대규모 데이터 및 실수 값 SSM 환경에서는 많은 초기화 방식이 잘 작동할 것으로 예상한다. 일부 ablation은 Section 4.6에서 다룬다.
의 파라미터화(Parameterization)
우리는 에 대한 **선택적 조정(selective adjustment)**을 로 정의했는데, 이는 의 메커니즘(Section 3.5)에 의해 동기 부여되었다. 우리는 이것이 차원 1에서 더 큰 차원 R로 일반화될 수 있음을 관찰한다. 우리는 이를 D의 작은 부분으로 설정하는데, 이는 블록 내의 주요 Linear projection에 비해 무시할 수 있는 수의 파라미터를 사용한다. 우리는 또한 broadcasting 연산이 1과 0의 특정 패턴으로 초기화된 또 다른 Linear projection으로 간주될 수 있음을 주목한다. 만약 이 projection이 학습 가능하다면, 이는 대안적인 로 이어지며, 이는 low-rank projection으로 볼 수 있다.
우리의 실험에서 파라미터(bias term으로 볼 수 있음)는 SSM에 대한 이전 연구 (Gu, Johnson, Timalsina, et al. 2023)에 따라 로 초기화된다.
Remark 3.1. 실험 결과의 간결성을 위해, 우리는 때때로 selective SSM을 S6 모델로 축약하여 부른다. 이는 S4 모델에 선택 메커니즘이 추가되었고 scan 방식으로 계산되기 때문이다.
4 Empirical Evaluation
Section 4.1에서는 Section 3.1에서 제시된 두 가지 합성 task를 Mamba가 해결하는 능력을 테스트한다. 이어서 세 가지 도메인에 대해 평가를 진행하며, 각 도메인에서는 autoregressive pretraining과 downstream task를 모두 평가한다.
- Section 4.2: language model pretraining (scaling laws) 및 zero-shot downstream 평가.
- Section 4.3: DNA sequence pretraining 및 long-sequence 분류 task에 대한 fine-tuning.
- Section 4.4: audio waveform pretraining 및 autoregressively 생성된 음성 클립의 품질.
마지막으로, Section 4.5에서는 Mamba의 학습 및 추론 시 계산 효율성을 보여주고, Section 4.6에서는 아키텍처 및 selective SSM의 다양한 구성 요소를 ablation한다.
4.1 Synthetic Tasks
이러한 task에 대한 전체 실험 세부 사항(task 세부 사항 및 학습 프로토콜 포함)은 Appendix E.1에 있다.
4.1.1 Selective Copying
Copying task는 순환 모델의 기억 능력을 테스트하기 위해 고안된, 시퀀스 모델링 분야에서 가장 잘 연구된 합성 task 중 하나이다. Section 3.1에서 논의했듯이, **LTI SSM(linear recurrences 및 global convolutions)**은 데이터에 대한 추론 대신 시간만 추적하는 방식으로 이 task를 쉽게 해결할 수 있다. 예를 들어, 정확히 올바른 길이의 convolution kernel을 구성하는 방식이다 (Figure 2). 이는 global convolutions에 대한 이전 연구(Romero et al. 2021)에서 명시적으로 검증되었다. Selective Copying task는 토큰 간의 간격을 무작위화하여 이러한 지름길을 방지한다. 이 task는 이전에 Denoising task(Jing et al. 2019)로 소개된 바 있다.
많은 이전 연구들은 아키텍처 gating(곱셈 상호작용)을 추가하면 모델에 "데이터 의존성"을 부여하고 관련 task를 해결할 수 있다고 주장한다 (Dao, Fu, Saab, et al. 2023; Poli et al. 2023). 그러나 우리는 이러한 설명이 직관적으로 불충분하다고 생각한다. 왜냐하면 이러한 gating은 시퀀스 축을 따라 상호작용하지 않으며, 토큰 간의 간격에 영향을 미칠 수 없기 때문이다. 특히 아키텍처 gating은 선택 메커니즘의 한 예시가 아니다 (Appendix A).
Table 1은 H3 및 Mamba와 같은 gated 아키텍처가 성능을 부분적으로만 향상시키는 반면, 선택 메커니즘(S4를 S6으로 수정)은 이 task를 쉽게 해결하며, 특히 이러한 더 강력한 아키텍처와 결합될 때 더욱 효과적임을 확인시켜 준다.
4.1.2 Induction Heads
Induction heads (Olsson et al. 2022)는 mechanistic interpretability (Elhage et al. 2021) 관점에서 볼 때, LLM의 in-context learning 능력을 놀랍도록 잘 예측하는 간단한 task이다. 이 task는 모델이 **연관 기억(associative recall) 및 복사(copy)**를 수행하도록 요구한다. 예를 들어, 모델이 시퀀스 내에서 "Harry Potter"와 같은 bigram을 본 적이 있다면, 다음에 동일한 시퀀스에서 "Harry"가 나타날 때, 모델은 이전 기록에서 "Potter"를 복사하여 예측할 수 있어야 한다.
데이터셋 (Dataset)
우리는 sequence length 256, vocab size 16으로 induction heads task에 대해 2-layer 모델을 학습시켰다. 이는 이 task에 대한 이전 연구 (Dao, Fu, Saab, et al. 2023)와 유사하지만, 더 긴 시퀀스를 사용했다. 또한, 테스트 시 부터 까지 다양한 sequence length로 평가하여 일반화(generalization) 및 외삽(extrapolation) 능력을 추가로 조사했다.
모델 (Models)
induction heads에 대한 기존 연구를 따라, 우리는 2-layer 모델을 사용했으며, 이는 attention이 induction heads task를 기계적으로 해결할 수 있도록 한다 (Olsson et al. 2022). 우리는 **multi-head attention (8개 head, 다양한 positional encoding)**과 SSM 변형을 모두 테스트했다. 모델 차원 는 Mamba의 경우 64, 다른 모델의 경우 128을 사용했다.
결과 (Results)
Table 2는 Mamba, 더 정확히는 Mamba의 selective SSM layer가 관련 토큰을 선택적으로 기억하고 그 사이의 모든 것을 무시하는 능력 덕분에 이 task를 완벽하게 해결할 수 있음을 보여준다. Mamba는 학습 시 본 시퀀스 길이보다 4000배 긴 백만 길이 시퀀스에 완벽하게 일반화되는 반면, 다른 어떤 방법도 2배 이상 일반화되지 못했다.
| Model | Arch. | Layer | Acc. |
|---|---|---|---|
| S4 | No gate | S4 | 18.3 |
| - | No gate | S6 | |
| H3 | H3 | S4 | 57.0 |
| Hyena | H3 | Hyena | 30.1 |
| - | H3 | S6 | |
| - | Mamba | S4 | 56.4 |
| - | Mamba | Hyena | 28.4 |
| Mamba | Mamba | S6 |
Table 1: (Selective Copying.)
아키텍처와 내부 시퀀스 레이어 조합에 대한 정확도.
 Table 2: (Induction Heads.)
Table 2: (Induction Heads.)
모델은 sequence length 으로 학습되었으며, 부터 까지 증가하는 sequence length에서 테스트되었다. 전체 수치는 Table 11에 있다.
 Figure 4: (Scaling Laws.)
Figure 4: (Scaling Laws.)
Pile 데이터셋으로 학습된 약 1.25억 개에서 약 13억 개 파라미터 규모의 모델들. Mamba는 다른 모든 attention-free 모델보다 더 잘 확장되며, 특히 sequence length가 길어질수록 현재 표준이 된 매우 강력한 "Transformer++" 레시피의 성능과 일치하는 최초의 모델이다.
attention 모델의 positional encoding 변형 중에서는 (길이 외삽을 위해 설계된) xPos가 다른 것들보다 약간 더 우수하다. 또한, 모든 attention 모델은 메모리 제한으로 인해 sequence length 까지만 테스트되었다는 점에 유의해야 한다. 다른 SSM 중에서는 H3와 Hyena가 유사하며, 이는 Poli et al. (2023)의 결과와는 상반된다.
4.2 Language Modeling
우리는 Mamba 아키텍처를 표준 autoregressive language modeling task에서 다른 아키텍처들과 비교 평가하였다. 평가는 **사전학습 지표(perplexity)**와 zero-shot 평가 모두에 대해 수행되었다. 모델 크기(깊이와 너비)는 GPT3 사양을 반영하도록 설정하였다. 우리는 **Pile 데이터셋 (L. Gao, Biderman, et al. 2020)**을 사용했으며, Brown et al. (2020)에 설명된 학습 레시피를 따랐다. 모든 학습 세부 사항은 Appendix E.2에 있다.
4.2.1 Scaling Laws
기준 모델로는 **표준 Transformer 아키텍처(GPT3 아키텍처)**와 우리가 아는 **가장 강력한 Transformer 레시피(여기서는 Transformer++로 지칭)**를 비교한다. Transformer++는 PaLM 및 LLaMa 아키텍처를 기반으로 하며, rotary embedding, SwiGLU MLP, LayerNorm 대신 RMSNorm 사용, linear bias 없음, 더 높은 learning rate 등의 특징을 포함한다. 또한, 다른 최근의 subquadratic 아키텍처들과도 비교한다 (Figure 4). 모든 모델의 세부 사항은 Appendix E.2에 있다.
Figure 4는 표준 Chinchilla (Hoffmann et al. 2022) 프로토콜에 따라 약 1억 2천 5백만 개에서 약 13억 개 파라미터에 이르는 모델들의 scaling law를 보여준다. Mamba는 sequence length가 길어질수록 특히 표준이 된 매우 강력한 Transformer 레시피(Transformer++)의 성능과 일치하는 최초의 attention-free 모델이다. (RWKV 및 RetNet 기준 모델의 경우, 효율적인 구현의 부재로 인해 메모리 부족 또는 비현실적인 계산 요구 사항이 발생하여 context length 8k에 대한 전체 결과가 누락되었음을 밝힌다. 이들은 강력한 recurrent 모델이며 SSM으로도 해석될 수 있다.)
4.2.2 Downstream Evaluations
Table 3는 Mamba의 다양한 인기 있는 downstream zero-shot 평가 task에서의 성능을 보여준다. 우리는 이 모델 크기에서 가장 잘 알려진 오픈 소스 모델들과 비교했으며, 특히 Pythia (Biderman et al. 2023)와 RWKV (B. Peng et al. 2023)는 우리 모델과 동일한 **tokenizer, dataset, 학습 길이 (300B tokens)**로 학습되었다는 점에서 중요하다. (참고로 Mamba와 Pythia는 context length 2048로 학습되었고, RWKV는 context length 1024로 학습되었다.)
Table 3: (Zero-shot 평가)
각 모델 크기별 최고 결과는 굵게(bold) 표시되었다. 우리는 다양한 tokenizer를 사용하고 최대 300B tokens까지 학습된 오픈 소스 LM들과 비교했다. Pile은 validation split을 의미하며, 동일한 dataset과 tokenizer (GPT-NeoX-20B)로 학습된 모델들하고만 비교했다. 각 모델 크기에서 Mamba는 모든 평가 결과에서 동급 최고(best-in-class)이며, 일반적으로 두 배 큰 모델 크기의 baseline과 동등한 성능을 보인다.
| Model | Token. | Pile ppl | LAMBADA PPL | LAMBADA ACC | HellaSwag ACC | PIQA ACC | Arc-E ACC | Arc-C ACC | WinoGrande ACC | Average Acc |
|---|---|---|---|---|---|---|---|---|---|---|
| Hybrid H3-130M | GPT2 | - | 89.48 | 25.77 | 31.7 | 64.2 | 44.4 | 24.2 | 50.6 | 40.1 |
| Pythia-160M | NeoX | 29.64 | 38.10 | 33.0 | 30.2 | 61.4 | 43.2 | 24.1 | 51.9 | 40.6 |
| Mamba-130M | NeoX | 10.56 | 16.07 | 44.3 | 35.3 | 64.5 | 48.0 | 24.3 | 51.9 | 44.7 |
| Hybrid H3-360M | GPT2 | - | 12.58 | 48.0 | 41.5 | 68.1 | 51.4 | 24.7 | 54.1 | 48.0 |
| Pythia-410M | NeoX | 9.95 | 10.84 | 51.4 | 40.6 | 66.9 | 52.1 | 24.6 | 53.8 | 48.2 |
| Mamba-370M | NeoX | 8.28 | 8.14 | 55.6 | 46.5 | 69.5 | 55.1 | 28.0 | 55.3 | 50.0 |
| Pythia-1B | NeoX | 7.82 | 7.92 | 56.1 | 47.2 | 70.7 | 57.0 | 27.1 | 53.5 | 51.9 |
| Mamba-790M | NeoX | 7.33 | 6.02 | 62.7 | 55.1 | 72.1 | 61.2 | 29.5 | 56.1 | 57.1 |
| GPT-Neo 1.3B | GPT2 | - | 7.50 | 57.2 | 48.9 | 71.1 | 56.2 | 25.9 | 54.9 | 52.4 |
| Hybrid H3-1.3B | GPT2 | - | 11.25 | 49.6 | 52.6 | 71.3 | 59.2 | 28.1 | 56.9 | 53.0 |
| OPT-1.3B | OPT | - | 6.64 | 58.0 | 53.7 | 72.4 | 56.7 | 29.6 | 59.5 | 55.0 |
| Pythia-1.4B | NeoX | 7.51 | 6.08 | 61.7 | 52.1 | 71.0 | 60.5 | 28.5 | 57.2 | 55.2 |
| RWKV-1.5B | NeoX | 7.70 | 7.04 | 56.4 | 52.5 | 72.4 | 60.5 | 29.4 | 54.6 | 54.3 |
| Mamba-1.4B | NeoX | 6.80 | 5.04 | 64.9 | 59.1 | 74.2 | 65.5 | 32.8 | 61.5 | 59.7 |
| GPT-Neo 2.7B | GPT2 | - | 5.63 | 62.2 | 55.8 | 72.1 | 61.1 | 30.2 | 57.6 | 56.5 |
| Hybrid H3-2.7B | GPT2 | - | 7.92 | 55.7 | 59.7 | 73.3 | 65.6 | 32.3 | 61.4 | 58.0 |
| OPT-2.7B | OPT | - | 5.12 | 63.6 | 60.6 | 74.8 | 60.8 | 31.3 | 61.0 | 58.7 |
| Pythia-2.8B | NeoX | 6.73 | 5.04 | 64.7 | 59.3 | 74.0 | 64.1 | 32.9 | 59.7 | 59.1 |
| RWKV-3B | NeoX | 7.00 | 5.24 | 63.9 | 59.6 | 73.7 | 67.8 | 33.1 | 59.6 | 59.6 |
| Mamba-2.8B | NeoX | 6.22 | 4.23 | 69.2 | 66.1 | 75.2 | 69.7 | 36.3 | 63.5 | 63.3 |
| GPT-J-6B | GPT2 | - | 4.10 | 68.3 | 66.3 | 75.4 | 67.0 | 36.6 | 64.1 | 63.0 |
| OPT-6.7B | OPT | - | 4.25 | 67.7 | 67.2 | 76.3 | 65.6 | 34.9 | 65.5 | 62.9 |
| Pythia-6.9B | NeoX | 6.51 | 4.45 | 67.1 | 64.0 | 75.2 | 67.3 | 35.5 | 61.3 | 61.7 |
| RWKV-7.4B | NeoX | 6.31 | 4.38 | 67.2 | 65.5 | 76.1 | 67.8 | 37.5 | 61.0 | 62.5 |
4.3 DNA Modeling
대규모 Language Model의 성공에 힘입어, 최근에는 유전체학(genomics) 분야에 foundation model 패러다임을 적용하려는 연구가 활발히 진행되고 있다. DNA는 유한한 어휘를 가진 이산적인 토큰 시퀀스로 구성된다는 점에서 언어에 비유되어 왔다. 또한 DNA는 장거리 의존성(long-range dependencies) 모델링이 필요한 것으로 알려져 있다 (Avsec et al. 2021).
우리는 DNA를 위한 long-sequence 모델에 대한 최근 연구들 (Nguyen, Poli, et al. 2023)과 동일한 설정에서, 사전학습(pretraining) 및 fine-tuning을 위한 FM backbone으로서 Mamba를 탐구한다. 특히, 우리는 모델 크기와 시퀀스 길이에 따른 scaling law (Figure 5), 그리고 긴 context를 요구하는 어려운 downstream 합성 분류 task (Figure 6)의 두 가지 탐구에 중점을 둔다.
사전학습의 경우, 우리는 표준적인 causal language modeling (다음 토큰 예측) 설정을 학습 및 모델 세부사항에 대부분 따른다 (Appendix E.2 참조). 데이터셋의 경우, HyenaDNA (Nguyen, Poli, et al. 2023)의 설정을 대부분 따르며, 이는 HG38 데이터셋을 사전학습에 사용한다. HG38은 약 45억 개의 토큰(DNA 염기쌍)으로 구성된 단일 인간 게놈을 학습 분할에 포함한다.
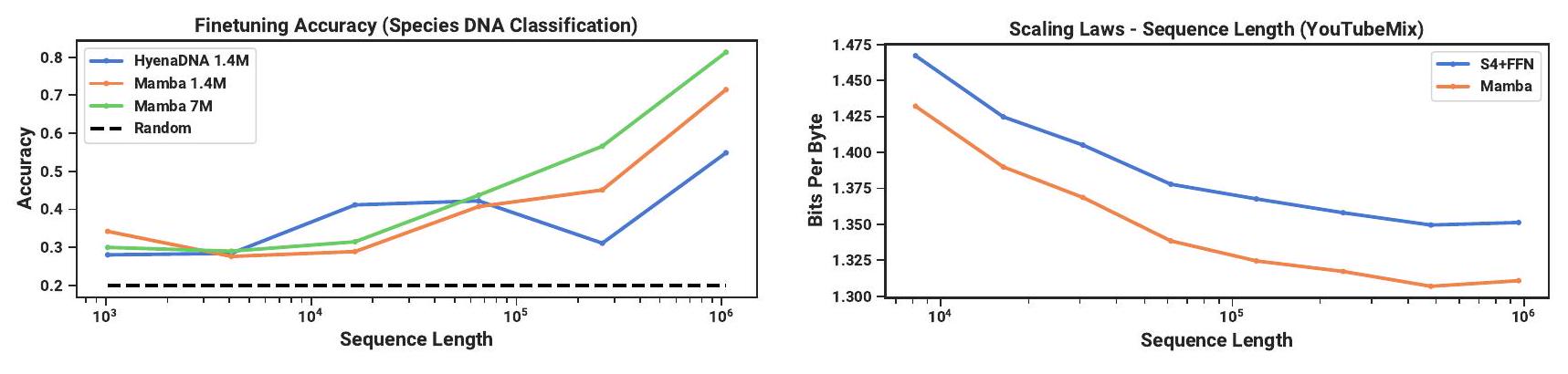
 Figure 5: (DNA Scaling Laws.) HG38 (인간 게놈) 데이터셋에 대한 사전학습 결과.
왼쪽: 짧은 context 길이 를 고정하고 모델 크기를 약 20만 개에서 약 4천만 개 파라미터로 증가시켰을 때, Mamba는 baseline보다 더 잘 확장된다.
오른쪽: 모델 크기를 고정하고 시퀀스 길이를 증가시키면서 tokens/batch와 총 학습 토큰 수를 고정했을 때. baseline과 달리, Mamba의 selection mechanism은 context 길이가 증가함에 따라 더 나은 성능을 촉진한다.
Figure 5: (DNA Scaling Laws.) HG38 (인간 게놈) 데이터셋에 대한 사전학습 결과.
왼쪽: 짧은 context 길이 를 고정하고 모델 크기를 약 20만 개에서 약 4천만 개 파라미터로 증가시켰을 때, Mamba는 baseline보다 더 잘 확장된다.
오른쪽: 모델 크기를 고정하고 시퀀스 길이를 증가시키면서 tokens/batch와 총 학습 토큰 수를 고정했을 때. baseline과 달리, Mamba의 selection mechanism은 context 길이가 증가함에 따라 더 나은 성능을 촉진한다.
4.3.1 Scaling: Model Size
이 실험에서는 다양한 모델 backbone을 가진 유전체학 foundation model의 스케일링 특성을 조사한다 (Figure 5 왼쪽).
학습 (Training)
baseline 모델에 유리하도록, 우리는 짧은 시퀀스 길이인 1024로 학습을 진행했다. Section 4.3.2에서 보여주듯이, 더 긴 시퀀스 길이에서는 Mamba가 훨씬 더 유리할 것으로 예상된다. 우리는 전역 batch size를 1024로 고정하여, batch당 총 토큰을 사용했다. 모델은 총 10K gradient step 동안 학습되었으며, 이는 총 10B 토큰에 해당한다.
결과 (Results)
Figure 5 (왼쪽)는 Mamba의 사전학습 perplexity가 모델 크기에 따라 부드럽게 향상되며, Mamba가 HyenaDNA와 Transformer++보다 더 잘 스케일링됨을 보여준다. 예를 들어, 약 40M 파라미터의 가장 큰 모델 크기에서, Mamba는 Transformer++ 및 HyenaDNA 모델과 거의 동일한 성능을 약 3배에서 4배 더 적은 파라미터로 달성할 수 있음을 곡선이 보여준다.
4.3.2 Scaling: Context Length
다음 DNA 실험에서는 시퀀스 길이에 따른 모델의 스케일링 특성을 조사한다. quadratic attention은 긴 시퀀스 길이에서 계산 비용이 너무 커지기 때문에, HyenaDNA와 Mamba 모델만 비교한다. 모델은 의 시퀀스 길이로 사전학습되었다. 모델 크기는 **6개 layer, 너비 128 (약 1.3M-1.4M 파라미터)**로 고정하였다. 모델은 총 20K gradient step 동안 학습되었으며, 이는 약 330B 토큰에 해당한다. 더 긴 시퀀스 길이에서는 (Nguyen, Poli, et al. 2023)과 유사하게 시퀀스 길이 warmup을 사용하였다.
결과. Figure 5 (오른쪽)는 Mamba가 1M에 달하는 극도로 긴 시퀀스에서도 긴 context를 활용할 수 있으며, context가 증가함에 따라 사전학습 perplexity가 향상됨을 보여준다. 반면, HyenaDNA 모델은 시퀀스 길이가 길어질수록 성능이 저하된다. 이는 Section 3.5의 selection mechanism 특성에 대한 논의와 일치한다. 특히, LTI 모델은 정보를 선택적으로 무시할 수 없다. convolutional 관점에서 보면, 매우 긴 convolution kernel은 매우 noisy할 수 있는 긴 시퀀스 전반의 모든 정보를 집계하게 된다. HyenaDNA는 더 긴 context에서 성능이 향상된다고 주장하지만, 그들의 결과는 계산 시간을 통제하지 않았다는 점에 유의해야 한다.
4.3.3 Synthetic Species Classification
우리는 모델을 DNA의 연속적인 세그먼트를 무작위로 샘플링하여 5가지 다른 종을 분류하는 다운스트림 task에서 평가한다. 이 task는 HyenaDNA에서 사용된 종인 {인간, 여우원숭이, 쥐, 돼지, 하마}에서 영감을 받아 수정되었다. 우리는 이 task를 다섯 가지 유인원 종인 {인간, 침팬지, 고릴라, 오랑우탄, 보노보}를 분류하도록 변경하여 훨씬 더 도전적인 task로 만들었다. 이들 종은 DNA의 99%를 공유하는 것으로 알려져 있다.
4.4 Audio Modeling and Generation
오디오 파형(audio waveform) 모달리티의 경우, 우리는 주로 SaShiMi 아키텍처 및 학습 프로토콜 (Goel et al. 2022)과 비교한다. 이 모델은 다음으로 구성된다:
- U-Net backbone: 각 단계에서 모델 차원 를 두 배로 늘리는 인자만큼의 두 단계 pooling을 포함한다.
- 각 단계에서 S4와 MLP 블록을 교대로 배치한다.
우리는 S4+MLP 블록을 Mamba 블록으로 대체하는 것을 고려한다. 실험 세부 사항은 Appendix E.4에 있다.
4.4.1 Long-Context Autoregressive Pretraining
우리는 사전학습 품질(autoregressive next-sample prediction)을 YouTubeMix (DeepSound 2017) 데이터셋으로 평가한다. 이 데이터셋은 이전 연구에서 사용된 표준 피아노 음악 데이터셋으로, 16000Hz로 샘플링된 4시간 분량의 솔로 피아노 음악으로 구성되어 있다. 사전학습 세부 사항은 대부분 표준 language modeling 설정을 따른다 (Section 4.2).
Figure 7은 연산량을 고정한 채 학습 시퀀스 길이를 에서 으로 늘렸을 때의 효과를 평가한다. (데이터 큐레이션 방식에 약간의 예외 사항이 있어 스케일링 곡선에 불규칙성이 나타날 수 있다. 예를 들어, 1분 길이의 클립만 사용 가능했기 때문에 실제 최대 시퀀스 길이는 으로 제한된다.)
Mamba와 SaShiMi (S4+MLP) baseline 모두 더 긴 context length에서 일관되게 성능이 향상된다. Mamba는 전반적으로 더 우수하며, 길이가 길어질수록 그 격차가 벌어진다. 주요 지표는 **bits per byte (BPB)**이며, 이는 다른 modality의 사전학습에 사용되는 표준 negative log-likelihood (NLL) loss에 의 상수 계수를 곱한 값이다.
한 가지 중요한 점은, 이 실험이 본 논문에서 유일하게 real parameterization에서 complex parameterization으로 전환한 경우라는 것이다 (Section 3.6). 추가적인 ablation 결과는 Appendix E.4에 제시되어 있다.
4.4.2 Autoregressive Speech Generation
SC09는 음성 생성 벤치마크 데이터셋으로 (Donahue, McAuley, and Puckette 2019; Warden 2018), "zero"부터 "nine"까지의 숫자를 16000Hz로 샘플링한 1초 길이의 음성 클립으로 구성되어 있으며, 매우 다양한 특성을 가진다. 우리는 Goel et al. (2022)의 autoregressive 학습 설정 및 생성 프로토콜을 대체로 따랐다.
Table 4는 Goel et al. (2022)의 다양한 baseline 모델들(WaveNet (Oord et al. 2016), SampleRNN (Mehri et al. 2017), WaveGAN (Donahue, McAuley, and Puckette 2019), DiffWave (Z. Kong et al. 2021), SaShiMi)과 비교한 Mamba-UNet 모델의 자동화된 metric 결과를 보여준다. 작은 Mamba 모델은 state-of-the-art 성능을 가진 (그리고 훨씬 큰) GAN 및 diffusion 기반 모델들을 능가한다. baseline 모델들과 파라미터 수가 일치하는 더 큰 Mamba 모델은 fidelity metric에서 더욱 극적으로 성능을 향상시킨다.
Table 5는 작은 Mamba 모델을 사용하여 outer stage와 center stage에 다른 아키텍처를 조합한 결과를 조사한다. 이 결과는 Mamba가 outer block에서 S4+MLP보다 일관되게 우수하며, center block에서는 Mamba > S4+MLP > MHA+MLP 순으로 성능이 좋음을 보여준다.
Table 4: (SC09) 고정 길이 음성 클립의 무조건부 생성에 대한 자동화된 metric 결과. (위에서 아래로) SaShiMi의 U-Net backbone, Autoregressive baseline, non-autoregressive baseline, Mamba, 그리고 데이터셋 metric.
Table 5: (SC09 모델 Ablation) 6M 파라미터를 가진 모델들. SaShiMi의 U-Net backbone에는 sequence length 1000에서 동작하는 8개의 center block이 있으며, 이 center block의 양쪽에는 sequence length 4000에서 동작하는 8개의 outer block이, 그리고 그 양쪽에는 sequence length 16000에서 동작하는 8개의 outer block이 배치되어 있다 (총 40개의 block). 8개의 center block 아키텍처는 나머지 부분과 독립적으로 ablation되었다. 효율성 제약으로 인해 Transformer (MHA+MLP)는 더 중요한 outer block에서는 테스트되지 않았다.
| Model | Params | NLL | FID | IS | mIS | AM |
|---|---|---|---|---|---|---|
| SampleRNN | 35.0 M | 2.042 | 8.96 | 1.71 | 3.02 | 1.76 |
| WaveNet | 4.2 M | 1.925 | 5.08 | 2.27 | 5.80 | 1.47 |
| SaShiMi | 5.8 M | 1.873 | 1.99 | 5.13 | 42.57 | 0.74 |
| WaveGAN | 19.1 M | - | 2.03 | 4.90 | 36.10 | 0.80 |
| DiffWave | 24.1 M | - | 1.92 | 5.26 | 51.21 | 0.68 |
| + SaShiMi | 23.0 M | - | 1.42 | 5.94 | 69.17 | 0.59 |
| Mamba | 6.1 M | 1.852 | 88.54 | |||
| Mamba | 24.3 M | 1.860 | 0.67 | 7.33 | 144.9 | 0.36 |
| Train | - | - | 0.00 | 8.56 | 292.5 | 0.16 |
| Test | - | - | 0.02 | 8.33 | 257.6 | 0.19 |
Table 4: (SC09) 고정 길이 음성 클립의 무조건부 생성에 대한 자동화된 metric 결과. (위에서 아래로) SaShiMi의 U-Net backbone, Autoregressive baseline, non-autoregressive baseline, Mamba, 그리고 데이터셋 metric.
Table 5: (SC09 모델 Ablation) 6M 파라미터를 가진 모델들. SaShiMi의 U-Net backbone에는 sequence length 1000에서 동작하는 8개의 center block이 있으며, 이 center block의 양쪽에는 sequence length 4000에서 동작하는 8개의 outer block이, 그리고 그 양쪽에는 sequence length 16000에서 동작하는 8개의 outer block이 배치되어 있다 (총 40개의 block). 8개의 center block 아키텍처는 나머지 부분과 독립적으로 ablation되었다. 효율성 제약으로 인해 Transformer (MHA+MLP)는 더 중요한 outer block에서는 테스트되지 않았다.
| Outer | Center | NLL | FID | IS | MIS | AM |
|---|---|---|---|---|---|---|
| S4+MLP | MHA+MLP | 1.859 | 1.45 | 5.06 | 47.03 | 0.70 |
| S4+MLP | S4+MLP | 1.867 | 1.43 | 5.42 | 53.54 | 0.65 |
| S4+MLP | Mamba | 1.859 | 1.42 | 5.71 | 56.51 | 0.64 |
| Mamba | MHA+MLP | 1.37 | 5.63 | 58.23 | 0.62 | |
| Mamba | S4+MLP | 1.853 | ||||
| Mamba | Mamba |
4.5 Speed and Memory Benchmarks
우리는 Figure 8에서 **SSM scan 연산의 속도(state expansion )**와 **Mamba의 end-to-end 추론 처리량(inference throughput)**을 벤치마크했다. 우리의 효율적인 SSM scan은 시퀀스 길이 2K를 넘어서면 우리가 아는 최고의 attention 구현(FlashAttention-2 (Dao 2024))보다 빠르며, PyTorch의 표준 scan 구현보다 최대 20-40배 빠르다. Mamba는 유사한 크기의 Transformer보다 4-5배 높은 추론 처리량을 달성하는데, 이는 KV cache가 없으므로 훨씬 더 높은 batch size를 사용할 수 있기 때문이다. 예를 들어, **Mamba-6.9B(미학습)**는 5배 작은 Transformer-1.3B보다 더 높은 추론 처리량을 가질 것이다. 자세한 내용은 Appendix E.5에 있으며, 여기에는 메모리 소비량 벤치마크도 추가로 포함되어 있다.
 Figure 8: (효율성 벤치마크.)
왼쪽: 학습(Training): 우리의 효율적인 scan은 표준 구현보다 40배 빠르다.
오른쪽: 추론(Inference): recurrent 모델인 Mamba는 Transformer보다 5배 높은 처리량을 달성할 수 있다.
Figure 8: (효율성 벤치마크.)
왼쪽: 학습(Training): 우리의 효율적인 scan은 표준 구현보다 40배 빠르다.
오른쪽: 추론(Inference): recurrent 모델인 Mamba는 Transformer보다 5배 높은 처리량을 달성할 수 있다.
4.6 Model Ablations
우리는 Chinchilla token count를 기준으로 약 350M 크기의 language modeling 설정(Figure 4와 동일한 설정)에 초점을 맞춰, 모델 구성 요소에 대한 일련의 상세한 ablation을 수행한다.
4.6.1 Architecture
Table 6은 아키텍처(블록)와 그 내부 SSM layer(Figure 3)의 효과를 조사한다. 우리는 다음을 발견했다:
- 이전의 비선택적(non-selective) LTI SSM(이는 전역 컨볼루션과 동일)들 사이에서는 성능이 매우 유사하다.
- 이전 연구의 복소수(complex-valued) S4 변형을 실수(real-valued) 변형으로 대체해도 성능에 큰 영향을 미치지 않는다. 이는 (적어도 LM의 경우) 하드웨어 효율성을 고려할 때 실수 SSM이 더 나은 선택일 수 있음을 시사한다.
- 이들 중 어느 것이든 선택적 SSM(S6)으로 대체하면 성능이 크게 향상되며, 이는 Section 3의 동기를 입증한다.
Table 6: (Ablations: 아키텍처 및 SSM Layer.) Mamba 블록은 H3와 유사한 성능을 보이면서도 더 간단하다. 내부 layer에서는 LTI 모델의 다양한 파라미터화 간에 차이가 거의 없지만, 선택적 SSM(S6)은 큰 성능 향상을 제공한다. 더 구체적으로, S4 (실수) 변형은 S4D-Real이고 S4 (복소수) 변형은 S4D-Lin이다.
| Model | Arch. | SSM Layer | Perplexity |
|---|---|---|---|
| Hyena | H3 | Hyena | 10.24 |
| H3 | H3 | S4 (complex) | 10.30 |
| - | H3 | S4 (real) | 10.34 |
| - | H3 | S6 |
| Model | Arch. | SSM Layer | Perplexity |
|---|---|---|---|
| - | Mamba | Hyena | 10.75 |
| - | Mamba | S4 (complex) | 10.54 |
| - | Mamba | S4 (real) | 10.56 |
| Mamba | Mamba | S6 |
Table 7: (Ablations: 선택적 파라미터.) 는 가장 중요한 파라미터(Theorem 1)이지만, 여러 선택적 파라미터를 함께 사용하면 시너지 효과를 낸다.
| Selective | Selective | Selective | Perplexity |
|---|---|---|---|
| 10.93 | |||
| 10.15 | |||
| 9.98 | |||
| 9.81 | |||
| 8.71 |
Table 8: (Ablations: 의 파라미터화.) SSM이 선택적일 때, S4D-Lin (Gu, Gupta, et al. 2022) 기반의 더 표준적인 초기화는 S4D-Real 또는 무작위 초기화보다 성능이 떨어진다.
| Initialization | Field | Perplexity |
|---|---|---|
| Complex | 9.16 | |
| Real | 8.85 | |
| Real | 8.71 | |
| Real | 8.71 |
- Mamba 아키텍처는 H3 아키텍처와 유사한 성능을 보이며 (선택적 layer를 사용할 때 약간 더 나은 것으로 보인다).
우리는 또한 Appendix E.2.2에서 Mamba 블록을 MLP(전통적인 아키텍처), MHA(하이브리드 attention 아키텍처)와 같은 다른 블록과 교차(interleaving)하는 방식도 조사한다.
4.6.2 Selective SSM
Table 7은 선택적 SSM layer를 선택적 파라미터(Algorithm 2)의 다양한 조합을 고려하여 ablation을 수행한 결과이다. 이 결과는 가 RNN gating과의 연결성(Theorem 1) 때문에 가장 중요한 파라미터임을 보여준다.
Table 8은 SSM의 다양한 초기화 방식을 고려한다. 초기화 방식은 일부 데이터 모달리티 및 설정에서 큰 차이를 보이는 것으로 알려져 있다 (Gu, Goel, and Ré 2022; Gu, Gupta, et al. 2022). 언어 모델링에서는 더 표준적인 복소수 파라미터화(S4D-Lin, 1행) 대신 더 간단한 실수 대각 초기화(S4D-Real, 3행)가 더 나은 성능을 보임을 확인했다. 무작위 초기화 또한 잘 작동하며, 이는 이전 연구(Mehta et al. 2023)의 결과와 일치한다.
Table 9와 Table 10은 각각 및 () projection의 차원 변화를 고려한다. 정적(static) 방식에서 선택적(selective) 방식으로 변경하는 것이 가장 큰 이점을 제공하며, 차원을 더 늘리는 것은 일반적으로 파라미터 수를 약간 증가시키면서 성능을 소폭 향상시킨다.
특히 주목할 만한 점은 state size 이 증가할 때 선택적 SSM의 성능이 극적으로 향상된다는 것이다. 단 1%의 추가 파라미터 비용으로 perplexity가 1.0 이상 개선되었다. 이는 Section 3.1과 3.3에서 제시된 우리의 핵심 동기를 입증한다.
5 Discussion
우리는 관련 연구, 한계점, 그리고 몇 가지 미래 방향에 대해 논의한다.
관련 연구 (Related Work)
Appendix A에서는 선택 메커니즘이 유사한 개념들과 어떻게 관련되는지를 논의한다. Appendix B에는 SSM 및 기타 관련 모델에 대한 확장된 관련 연구가 포함되어 있다.
Table 9: (Ablation: 의 표현력)
의 선택 메커니즘은 입력의 projection으로 구성된다. 차원 1로만 projection해도 성능이 크게 향상되며, 이를 더 늘리면 파라미터가 약간 증가하는 대신 추가적인 성능 향상을 가져온다. State size는 으로 고정되었다.
| Size of proj. | Params (M) | Perplexity |
|---|---|---|
| - | 358.9 | 9.12 |
| 1 | 359.1 | 8.97 |
| 2 | 359.3 | 8.97 |
| 4 | 359.7 | 8.91 |
| 8 | 360.5 | 8.83 |
| 16 | 362.1 | 8.84 |
| 32 | 365.2 | 8.80 |
| 64 | 371.5 | 8.71 |
Table 10: (Ablation: SSM state dimension)
(상단) 와 가 고정된 경우 (하단) 와 가 선택적인 경우.
SSM state dimension 을 증가시키는 것은 recurrent state의 차원 확장 계수로 볼 수 있으며, 파라미터/FLOPs 비용이 거의 없이 성능을 크게 향상시킬 수 있다. 하지만 이는 와 또한 선택적일 때만 해당된다. projection의 크기는 64로 고정되었다.
| State dimension | Params (M) | Perplexity |
|---|---|---|
| 1 | 367.1 | 9.88 |
| 2 | 367.4 | 9.86 |
| 4 | 368.0 | 9.82 |
| 8 | 369.1 | 9.82 |
| 16 | 371.5 | 9.81 |
| 1 | 367.1 | 9.73 |
| 2 | 367.4 | 9.40 |
| 4 | 368.0 | 9.09 |
| 8 | 369.1 | 8.84 |
| 16 | 371.5 | 8.71 |
No Free Lunch: 연속-이산 스펙트럼 (Continuous-Discrete Spectrum)
Structured SSM은 원래 **연속 시스템의 이산화(discretization)**로 정의되었으며 (1), 지각 신호(예: 오디오, 비디오)와 같은 연속 시간 데이터 양식에 강한 inductive bias를 가지고 있었다. Section 3.1과 3.5에서 논의했듯이, 선택 메커니즘은 텍스트 및 DNA와 같은 이산 양식에서의 약점을 극복하지만, 반대로 LTI SSM이 뛰어난 데이터에서는 성능을 저해할 수 있다. 오디오 파형에 대한 우리의 ablation은 이러한 trade-off를 더 자세히 조사한다.
다운스트림 활용성 (Downstream Affordances)
Transformer 기반 foundation model(특히 LLM)은 fine-tuning, adaptation, prompting, in-context learning, instruction tuning, RLHF, quantization 등 사전학습된 모델과의 상호작용을 위한 풍부한 생태계와 속성을 가지고 있다. 우리는 특히 SSM과 같은 Transformer 대안이 유사한 속성과 활용성을 가지는지에 관심이 있다.
확장성 (Scaling)
우리의 실험적 평가는 작은 모델 크기에 국한되어 있으며, 이는 대부분의 강력한 오픈 소스 LLM(예: Llama (Touvron et al. 2023))뿐만 아니라 7B 파라미터 규모 이상에서 평가된 RWKV (B. Peng et al. 2023) 및 RetNet (Y. Sun et al. 2023)과 같은 다른 recurrent model의 임계값보다 낮다. Mamba가 이러한 더 큰 규모에서도 여전히 유리한 비교 우위를 가질지는 추가적인 평가가 필요하다. 또한, SSM의 확장은 본 논문에서 논의되지 않은 추가적인 엔지니어링 문제 및 모델 조정을 포함할 수 있음을 언급한다.
6 Conclusion
우리는 structured state space model에 **선택 메커니즘(selection mechanism)**을 도입하여, 시퀀스 길이에 선형적으로 확장되면서도 문맥 의존적인 추론(context-dependent reasoning)을 수행할 수 있도록 하였다. 이 메커니즘을 간단한 attention-free 아키텍처에 통합했을 때, Mamba는 다양한 도메인에서 state-of-the-art 결과를 달성하며, 강력한 Transformer 모델의 성능과 동등하거나 그 이상을 보여주었다. 우리는 선택적 state space model이 다양한 도메인을 위한 foundation model을 구축하는 데, 특히 유전체학, 오디오, 비디오와 같이 긴 context를 요구하는 새로운 modality에서 광범위하게 적용될 수 있음에 큰 기대를 걸고 있다. 우리의 결과는 Mamba가 범용 시퀀스 모델의 backbone으로서 강력한 후보임을 시사한다.
Acknowledgments
초고에 대한 유용한 피드백을 제공해 준 Karan Goel, Arjun Desai, Kush Bhatia에게 감사드린다.
A Discussion: Selection Mechanism
우리의 **선택 메커니즘(selection mechanism)**은 gating, hypernetworks, data-dependence와 같은 개념들에서 영감을 받았으며 이들과 관련이 있다. 또한 이는 "fast weights" (J. Ba et al. 2016; Schmidhuber 1992)와도 관련이 있다고 볼 수 있는데, 이는 고전적인 RNN과 linear attention 메커니즘 (Schlag, Irie, and Schmidhuber 2021)을 연결한다. 그러나 우리는 이것이 명확히 할 가치가 있는 별개의 개념이라고 생각한다.
Gating. Gating은 원래 LSTM (Hochreiter and Schmidhuber 1997) 및 GRU (J. Chung et al. 2014)와 같은 RNN의 gating 메커니즘 또는 **Theorem 1의 gated equation (5)**를 지칭했다. 이는 입력을 RNN의 hidden state로 들여보낼지 여부를 제어하는 특정 메커니즘으로 해석되었다. 특히, 이는 시간에 따른 신호 전파에 영향을 미치고 입력이 시퀀스 길이 차원을 따라 상호작용하도록 한다.
그러나 gating의 개념은 대중적인 사용에서 단순히 모든 곱셈 상호작용(종종 활성화 함수와 함께)을 의미하도록 완화되었다. 예를 들어, **신경망 아키텍처의 요소별 곱셈 구성 요소(시퀀스 길이를 따라 상호작용하지 않는)**는 이제 gated 아키텍처라고 일반적으로 불린다 (Hua et al. 2022; Mehta et al. 2023). 이는 원래의 RNN 의미와는 매우 다른 의미임에도 불구하고 그렇다. 따라서 우리는 RNN gating의 원래 개념과 곱셈 gating의 대중적인 사용이 실제로 매우 다른 의미론적 의미를 가진다고 생각한다.
Hypernetworks. Hypernetworks는 매개변수 자체가 더 작은 신경망에 의해 생성되는 신경망을 의미한다. 원래 아이디어 (Ha, Dai, and Quoc V. Le 2017)는 더 작은 RNN에 의해 recurrent 매개변수가 생성되는 큰 RNN을 정의하는 좁은 의미로 사용되었으며, 다른 변형들은 오랫동안 존재해왔다 (Schmidhuber 1992).
Data-dependence. Hypernetworks와 유사하게, data-dependence는 모델의 일부 매개변수가 데이터에 의존하는 모든 개념을 지칭할 수 있다 (Poli et al. 2023).
예시: GLU Activation. 이러한 개념들의 문제점을 설명하기 위해, **대각선 가중치 매개변수 를 가진 간단한 대각선 선형 레이어 **를 고려해보자. 이제 가 의 선형 변환으로부터 선택적인 비선형성 와 함께 생성된다고 가정해보자. 대각선이므로 곱셈은 요소별 곱셈이 된다: .
이것은 다소 사소한 변환이지만, **gating(곱셈 "분기"가 있으므로), hypernetworks(매개변수 가 다른 레이어에 의해 생성되므로), data-dependent( 가 데이터 에 의존하므로)**의 일반적인 의미를 기술적으로 만족한다. 그러나 이것은 사실 단순히 GLU 함수를 정의하며, 이는 너무 간단하여 의미 있는 레이어라기보다는 종종 활성화 함수로 간주된다 (Dauphin et al. 2017; Shazeer 2020).
Selection. 따라서, **선택 메커니즘(selection mechanisms)**은 아키텍처 gating, hypernetworks, data-dependence와 같은 아이디어의 특수한 경우로 간주될 수 있지만, 표준 attention 메커니즘 (Bahdanau, Cho, and Bengio 2015; Vaswani et al. 2017)을 포함하여 곱셈이 있는 모든 다른 구성도 마찬가지이며, 우리는 그것들을 그렇게 생각하는 것이 정보적이지 않다고 생각한다.
대신, 우리는 이를 전통적인 RNN의 gating 메커니즘과 가장 밀접하게 관련되어 있다고 본다. 이는 특수한 경우 (Theorem 1)이며, 의 가변(입력 의존적) 이산화를 통해 SSM과 더 깊은 연결의 역사를 가지고 있다 (Funahashi and Nakamura 1993; Gu, Dao, et al. 2020; Tallec and Ollivier 2018). 우리는 또한 "gating"이라는 용어의 과부하된 사용을 명확히 하기 위해 selection이라는 용어를 선호한다. 더 좁게는, 우리는 selection을 모델이 입력을 선택하거나 무시하고 시퀀스 길이를 따라 데이터 상호작용을 촉진하는 기계적 동작을 지칭하는 데 사용한다 (Section 3.1). selective SSM과 gated RNN 외의 다른 예시로는 입력 의존적 convolution (Kosma, Nikolentzos, and Vazirgiannis 2023; Lioutas and Guo 2020; Lutati, Zimerman, and Wolf 2023; Yang et al. 2019) 및 attention도 포함될 수 있다.
B Related Work
우리는 우리의 방법과 관련된 여러 선행 연구들을 개괄적으로 살펴본다. 가장 밀접하게 관련된 모델들 중 일부는 S4, S5, quasi-RNN과 같은 recurrent layer를 포함하며, H3, RetNet, RWKV와 같은 end-to-end 아키텍처도 포함된다.
B. 1 S4 Variants and Derivatives
우리는 과거 연구에서 제안된 일부 structured SSM에 대해 간략히 설명하며, 특히 우리의 방법과 관련 있는 모델들을 중심으로 다룬다.
- S4 (Gu, Goel, and Ré 2022; Gu, Johnson, Goel, et al. 2021)는 최초의 structured SSM을 소개하며, diagonal structure와 diagonal plus low-rank (DPLR) 구조를 설명했다. 이 연구는 continuous-time online memorization (HIPPO) (Gu, Dao, et al. 2020)과의 연관성 때문에 DPLR SSM을 위한 효율적인 convolutional algorithm에 중점을 두었다.
- DSS (Gupta, Gu, and Berant 2022)는 HIPPO initialization을 근사함으로써 diagonal structured SSM의 실증적 효과를 처음으로 발견했다. 이는 S4D (Gu, Gupta, et al. 2022)에서 이론적으로 확장되었다.
- S5 (Smith, Warrington, and Linderman 2023)는 diagonal SSM 근사를 독립적으로 발견했으며, parallel scan을 사용하여 recurrent하게 계산된 최초의 S4 모델이다. 그러나 이는 효과적인 state dimension을 낮춰야 하는 문제가 있었고, 이를 SSM dimension을 SISO (single-input single-output)에서 MIMO (multi-input multi-output) 형태로 전환하여 해결했다. 우리가 제안하는 S6는 scan을 공유하지만, 다음과 같은 점에서 차이가 있다: (i) SISO dimension을 유지하여 더 큰 효과적인 recurrent state를 제공한다. (ii) hardware-aware algorithm을 사용하여 계산 문제를 극복한다. (iii) selection mechanism을 추가한다.
Lu et al. (2023)은 에피소드 trajectory 간에 SSM state를 재설정하기 위해 S5를 meta-RL에 적용했다. 그들의 메커니즘은 특정 hard-coded selection mechanism의 한 예시로 볼 수 있으며, 여기서 는 입력에 의존하는 우리의 학습 가능한 메커니즘 대신 수동으로 0으로 설정된다. 이 설정에 selective SSM을 일반적으로 적용하여 모델이 에피소드 경계에서 자동으로 state를 재설정하는 방법을 학습했는지 탐색하는 것은 흥미로운 연구가 될 것이다.
- Mega (Ma et al. 2023)는 S4를 복소수(complex-valued) 대신 실수(real-valued)로 단순화하여 exponential moving average (EMA)로 해석될 수 있도록 했다. 그들은 또한 SSM의 이산화(discretization) 단계와 EMA damping term 간의 흥미로운 연결을 만들었다. 원래 S4 논문의 발견과는 달리, 이 모델은 실수(real-valued) SSM이 특정 설정에서 또는 다른 아키텍처 구성 요소와 결합될 때 실증적으로 효과적임을 보여준 최초의 모델이다.
- Liquid S4 (Hasani et al. 2023) 또한 입력 의존적인 state transition으로 S4를 보강하는 데 동기를 부여받았다. 이러한 관점에서 이는 selection mechanism과 유사성을 공유하지만, 여전히 convolutional하게 계산되고 LTI에 가까운 제한된 형태이다.
- SGConv (Y. Li et al. 2023), Hyena (Poli et al. 2023), LongConv (Fu et al. 2023), MultiresConv (J. Shi, K. A. Wang, and Fox 2023), Toeplitz Neural Network (Qin, Han, W. Sun, B. He, et al. 2023)는 모두 S4의 convolutional representation에 중점을 두며, 다양한 parameterization을 가진 global 또는 long convolution kernel을 생성한다. 그러나 이러한 방법들은 빠른 autoregressive inference를 직접 수행할 수 없다.
주목할 만한 점은, 이 모든 방법들과 우리가 아는 다른 모든 structured SSM들은 non-selective였으며, 일반적으로 **엄격하게 LTI (linear time invariant)**였다는 것이다.
B. 2 SSM Architectures
우리는 SSM 아키텍처 또는 state space neural network (SSNN) 라는 용어를 사용하여 이전 SSM 중 하나를 블랙박스 레이어로 통합하는 심층 신경망 아키텍처를 지칭한다.
- **GSS (Mehta et al. 2023)**는 SSM을 통합한 최초의 gated neural network 아키텍처였다. 이는 Hua et al. (2022)의 **gated attention unit (GAU)**에서 영감을 받았으며, 추가적인 projection을 제외하면 우리 블록과 상당히 유사하다. 가장 중요한 차이점은, GSS의 projection은 모델 차원을 축소하여 SSM의 state 크기를 줄이는 반면, 우리의 방식은 Section 3.1의 동기에 따라 모델 차원을 확장하여 state 크기를 늘린다는 점이다.
- **Mega (Ma et al. 2023)**는 위에서 설명한 S4의 EMA 단순화를 효율적인 attention 근사치를 사용하는 하이브리드 아키텍처에 결합했다.
- **H3 (Dao, Fu, Saab, et al. 2023)**는 S4와 **linear attention (Katharopoulos et al. 2020)**을 결합하는 데서 영감을 받았다. 이는 linear attention의 이러한 공식을 더 일반적인 recurrence로 일반화한 최초의 연구이며, 이는 이후 아키텍처의 기반이 되기도 한다.
- **Selective S4 (J. Wang et al. 2023)**는 S4를 블랙박스로 통합하여 입력에 곱해지는 이진 마스크(binary mask)를 생성한다. "selection"이라는 이름을 공유하지만, 우리는 이를 선택 메커니즘보다는 아키텍처적 게이팅에 더 가까운 아키텍처 수정으로 간주한다 (Appendix A). 예를 들어, 우리는 이것이 Selective Copying task를 해결하지 못할 것이라고 가정한다. 왜냐하면 관련 없는 입력을 단순히 마스킹하는 것은 관련 있는 입력들 사이의 간격에 영향을 미치지 않기 때문이다 (실제로 Selective Copying task는 노이즈 토큰이 0으로 임베딩되면 미리 마스킹된 것으로 간주될 수도 있다).
- RetNet (Y. Sun et al. 2023) 또한 Linear Attention을 기반으로 하며 H3와 매우 유사하지만, 내부 S4 레이어를 state 차원이 인 특수한 경우로 축소한다. 비록 그렇게 구성되지는 않았지만, 그 recurrence는 선형 SSM의 특수한 경우로 볼 수 있다.
RetNet의 주요 개선점은 큰 head dimension을 가진 linear attention을 사용하는 것인데, 이는 입력 의존적인 state 확장을 수행하는 또 다른 방법으로 볼 수 있다. linear attention 변형에서 더 큰 head dimension을 사용하는 것은 H3에서 처음 시도되었지만, 비례적인 추가 계산이 필요하기 때문에 광범위하게 사용되지는 않았다. RetNet은 표준 multi-head attention의 변형을 사용하여 계산을 병렬화하는 대체 방식으로 이를 피하는데, 이는 단순한 EMA 역할을 하는 SSM의 특정 특수 사례 덕분에 가능해졌다.
- **RWKV (B. Peng et al. 2023)**는 언어 모델링을 위해 설계된 또 다른 최신 RNN이다. 이는 **AFT (attention-free Transformer (S. Zhai et al. 2021))**를 기반으로 하며, 이는 linear attention의 또 다른 변형이다. RWKV의 주요 "WKV" 메커니즘은 LTI recurrence를 포함하며, 두 SSM의 비율로 볼 수 있다.
우리는 또한 **Transformer의 MHA와 MLP 블록을 결합하는 데서 영감을 받아 우리 아키텍처(Section 3.4)의 H3와 MLP 블록을 결합하는 데 영감을 준 Hua et al. (2022)의 gated attention unit (GAU)**을 강조한다.
B. 3 Relationship to RNNs
RNN과 SSM은 모두 잠재 상태(latent state)에 대한 recurrence 개념을 포함한다는 점에서 넓게 연관되어 있다. strongly typed RNN (Balduzzi and Ghifary 2016), quasi-RNN (QRNN) (Bradbury et al. 2016), simple recurrent unit (SRU) (Lei 2021; Lei et al. 2017)과 같은 몇몇 오래된 RNN들은 시간에 따른 비선형성(time-wise nonlinearities)이 없는 gated RNN의 형태를 포함한다. gating mechanism과 selection mechanism의 연결성 때문에, 이들은 selective SSM의 한 경우로 볼 수 있으며, 따라서 위에서 언급된 LTI structured SSM 계열보다 어떤 의미에서는 더 강력하다. 주요 차이점은 다음과 같다:
- 이들은 **state expansion ()**이나 selective 파라미터를 사용하지 않는데, 이 두 가지 모두 성능에 중요하다 (Section 4.6).
- 이들은 휴리스틱한 gating mechanism을 사용하는데, 우리는 이를 selection mechanism + discretization의 결과로 일반화한다 (Theorem 1). 원칙적인 SSM 이론과의 연결은 더 나은 parameterization과 initialization을 제공한다 (Section 3.6).
또한, 오래된 RNN들은 효율성 문제와 vanishing gradients 문제로 유명하게 고통받았는데 (Hochreiter 1991; Hochreiter, Bengio, et al. 2001; Pascanu, Mikolov, and Bengio 2013), 이 두 가지 모두 순차적인 특성 때문에 발생했다. 전자는 위 RNN 중 일부에서 parallel scan을 활용하여 해결할 수 있었지만 (Martin and Cundy 2018), 후자는 SSM을 위해 나중에 개발된 이론 없이는 어려웠다. 예를 들어, 현대적인 structured SSM은 고전적인 SSM 이론에서 영감을 받은 recurrent dynamics의 더 신중한 parameterization (예: discretization을 통해 (Gu, Johnson, Goel, et al. 2021; Gu, Johnson, Timalsina, et al. 2023)) 또는 직접적인 분석 (Gupta, Mehta, and Berant 2022; Kaul 2020; Orvieto et al. 2023)에서 차이를 보인다.
우리는 또한 orthogonal RNN에 대한 오랜 연구 계보가 있다는 점에 주목한다 (Arjovsky, Shah, and Bengio 2016; Henaff, Szlam, and LeCun 2016; Lezcano-Casado and Martínez-Rubio 2019; Mhammedi et al. 2017; Vorontsov et al. 2017). 이들은 transition matrix를 orthogonal 또는 unitary로 제약하여 고유값(eigenvalues)을 제어하고 vanishing gradient 문제를 방지하려는 동기에서 시작되었다. 그러나 이들은 다른 한계점을 가지고 있었는데, 우리는 이러한 한계점이 orthogonal/unitary RNN 또한 LTI라는 사실에서 비롯된다고 생각한다. 예를 들어, 이들은 거의 항상 Copying task에서 평가되며 이 task는 완벽하게 해결할 수 있지만, Selective Copying task에서는 어려움을 겪는 것으로 관찰되었다 (Jing et al. 2019).
B. 4 Linear Attention
Linear Attention (LA) [Katharopoulos et al. 2020] 프레임워크는 kernel attention을 대중화하고, 이것이 recurrent autoregressive model과 어떻게 관련되는지를 보여준 중요한 연구 결과이다. 많은 변형 모델들이 대체 kernel이나 다른 수정 사항들을 제안해왔다.
- Random Feature Attention (RFA) [H. Peng et al. 2021]은 softmax attention을 근사하기 위해 kernel feature map을 선택하며, Gaussian kernel의 random Fourier feature approximation [Rahimi and Recht 2007]을 사용한다.
- Performer [Choromanski et al. 2021]는 양수 feature만을 포함하는 exponential kernel의 근사를 찾아내어, softmax normalization term을 가능하게 한다.
- TransNormer [Qin, Han, W. Sun, D. Li, et al. 2022]는 LA의 분모(denominator) 항이 불안정할 수 있음을 보여주며, 이를 LayerNorm으로 대체할 것을 제안했다.
- cosFormer [Qin, W. Sun, et al. 2022]는 RFA에 cosine reweighting mechanism을 추가하여 위치 정보(positional information)를 통합하고 locality를 강조한다.
- Linear Randomized Attention [Zheng, C. Wang, and L. Kong 2022]은 importance sampling 관점에서 RFA를 일반화하고, 전체 softmax kernel에 대한 더 나은 추정치를 제공하도록 확장한다 (단순히 exp-변환된 분자(numerator)가 아닌).
kernel attention 외에도, 다양한 효율적인 attention 변형 모델들이 존재한다. Tay, Dehghani, Bahri, et al. [2022]의 설문조사는 이들 중 많은 부분을 광범위하게 분류하여 제시한다.
B. 5 Long Context Models
Long context는 최근 인기 있는 주제가 되었으며, 여러 최신 모델들이 점점 더 긴 시퀀스로 확장될 수 있다고 주장해왔다. 그러나 이러한 주장들은 종종 계산적인 관점에서 이루어졌으며, 광범위하게 검증되지는 않았다. 여기에는 다음 모델들이 포함된다:
- Recurrent Memory Transformer (Bulatov, Kuratov, and Burtsev 2023): Transformer backbone을 감싸는 경량 wrapper이다. 이 모델은 최대 1M 시퀀스까지 일반화하는 능력을 보였지만, 합성(synthetic) 기억 task에서만 그러했다. 그들의 주요 결과는 우리의 Induction Heads extrapolation 실험 (Table 2)과 유사하다.
- LongNet (Ding et al. 2023): 1B 길이까지 확장 가능하다고 주장했지만, 실제 task에서는 100K 미만의 길이에서만 평가되었다.
- Hyena 및 HyenaDNA (Nguyen, Poli, et al. 2023; Poli et al. 2023): 최대 1M context를 활용한다고 주장했다. 그러나 이들의 실험은 더 긴 context에서 비례적으로 더 많은 데이터로 학습되었기 때문에, 1M context에서의 품질 향상이 context 길이 때문인지, 아니면 더 많은 데이터와 계산량 때문인지 결론 내리기 어렵다.
- Sparse Transformer (Child et al. 2019): strided sparse attention Transformer를 사용하여 길이의 오디오 파형을 모델링하는 개념 증명을 보였지만, 계산량과 모델 크기를 제어했을 때의 성능 trade-off에 대해서는 논의하지 않았다.
이와 대조적으로, 우리는 본 연구가 더 긴 context에서 의미 있는 성능 향상을 보여주는 최초의 접근 방식 중 하나라고 생각한다.
C Mechanics of Selective SSMs
정리 1의 증명.
softplus를 갖는 selective SSM (Algorithm 2)을 고려한다.
해당하는 연속 시간 SSM (1)은 다음과 같다:
이는 leaky integrator라고도 불린다.
이때 이산화(discretization) 스텝 크기는 다음과 같다:
여기서 Parameter는 학습 가능한 bias로 간주되어 linear projection에 통합될 수 있음을 알 수 있다.
이제 zero-order hold (ZOH) 이산화 공식을 적용하면 다음과 같다:
따라서 최종 이산 재귀식 (2a)는 다음과 같다:
이는 우리가 원하는 결과이다.
D Hardware-aware Algorithm For Selective SSMs
input-dependent selectivity가 없는 경우, SSM은 convolution으로 효율적으로 구현될 수 있으며 (Dao, Fu, Saab, et al. 2023; Gu, Goel, and Ré 2022), 이는 **고속 푸리에 변환(FFT)**을 기본 연산으로 활용한다. selectivity가 있는 경우, SSM은 더 이상 convolution과 동등하지 않지만, 우리는 병렬 associative scan을 활용한다. SSM scan은 이론적으로 효율적이지만 ( FLOPs, 에 선형적으로 확장), selective SSM을 사용하는 foundation model을 학습시키려면 최신 하드웨어(GPU)에서도 효율적이어야 한다. 우리는 kernel fusion과 recomputation을 사용하여 SSM scan을 빠르고 메모리 효율적으로 만드는 방법을 설명한다. Section 4.5에서는 convolution 및 attention과 비교하여 우리 scan 구현의 속도를 평가하며, 시퀀스 길이 32K에서 attention보다 최대 7배 빠르고, 최고의 attention 구현(FlashAttention)만큼 메모리 효율적임을 보여준다.
속도 (Speed)
최신 하드웨어 가속기(GPU)에서 대부분의 연산(행렬 곱셈 제외)은 **메모리 대역폭(memory bandwidth)**에 의해 제한된다 (Dao, Fu, Ermon, et al. 2022; Ivanov et al. 2021; Williams, Waterman, and Patterson 2009). 이는 우리의 scan 연산에도 해당되며, 우리는 kernel fusion을 사용하여 메모리 IO 양을 줄여 표준 구현에 비해 상당한 속도 향상을 이끌어냈다.
Section 3.2의 scan 알고리즘을 구현하는 표준 방식은 다음과 같다:
- GPU HBM(고대역폭 메모리, 일반적으로 GPU 메모리라고 함)에 크기의 scan 입력 를 준비한다.
- 병렬 associative scan 구현을 호출하여 크기의 scan 출력을 GPU HBM에 기록한다.
- 해당 scan 출력에 를 곱하여 크기의 출력을 생성한다.
그러나 이 방식은 수준의 메모리 읽기/쓰기를 필요로 한다. 대신, 이산화(discretization) 단계, scan, 그리고 와의 곱셈을 하나의 kernel로 융합할 수 있다:
- 느린 HBM에서 빠른 SRAM으로 바이트의 메모리()를 읽어온다.
- SRAM에서 크기의 를 생성하기 위해 이산화를 수행한다.
- 병렬 associative scan을 수행하여 SRAM에 크기의 중간 상태를 생성한다.
- 와 곱하고 합산하여 크기의 출력을 생성하고 이를 HBM에 기록한다.
이러한 방식으로 우리는 IO를 (상태 차원)만큼 줄여, 실제로는 연산 속도를 20-40배 향상시킨다 (Section 4.5).
시퀀스 길이 이 너무 길어 SRAM(HBM보다 훨씬 작음)에 시퀀스를 담을 수 없는 경우, 시퀀스를 청크(chunk)로 분할하고 각 청크에 대해 융합된 scan을 수행한다. 중간 scan 상태만 있다면 다음 청크로 scan을 계속할 수 있다.
메모리 (Memory)
우리는 recomputation이라는 고전적인 기술을 사용하여 selective SSM layer를 학습하는 데 필요한 총 메모리 양을 줄이는 방법을 설명한다.
forward pass를 융합하는 방식 때문에, 메모리 폭증을 피하기 위해 크기의 중간 상태를 저장하지 않는다. 그러나 이 중간 상태는 backward pass에서 gradient를 계산하는 데 필수적이다. 우리는 대신 **backward pass에서 이 중간 상태를 재계산(recompute)**한다. HBM에서 SRAM으로 읽어오는 입력 및 출력 gradient의 크기는 이고, 입력 gradient 또한 이므로, 재계산은 HBM에서 요소를 읽는 비용을 피하게 해준다. 이는 backward pass에서 SSM 상태를 재계산하는 것이, 이를 저장하고 HBM에서 읽는 것보다 계산 속도를 높여준다는 것을 의미한다.
scan 연산 자체의 메모리 요구 사항을 최적화하는 것을 넘어, 우리는 recomputation을 사용하여 전체 selective SSM 블록(input projection, convolution, activation, scan, output projection)의 메모리 요구 사항을 최적화한다. 특히, 많은 메모리를 차지하지만 재계산이 빠른 중간 activation(예: activation 함수의 출력 또는 짧은 convolution)은 저장하지 않는다. 결과적으로, selective SSM layer는 FlashAttention을 사용한 최적화된 Transformer 구현과 동일한 메모리 요구 사항을 가진다. 특히, 각 attention layer(FlashAttention)는 토큰당 약 12바이트의 activation을 저장하고, 각 MLP layer는 토큰당 약 20바이트의 activation을 저장하여 총 32바이트를 차지한다(FP16 또는 BF16 혼합 정밀도 학습 가정). 각 selective SSM은 토큰당 약 16바이트의 activation을 저장한다. 따라서 두 개의 selective SSM layer는 attention layer와 MLP layer의 activation 메모리와 거의 동일한 양을 가진다.
Table 11: (Induction heads.) 모델은 시퀀스 길이 으로 학습되었으며, 부터 까지 다양한 시퀀스 길이에서 테스트되었다. 는 완벽한 일반화 정확도를 나타내고, 는 메모리 부족(out of memory)을 나타낸다.
| Model | Params | Test Accuracy (%) at Sequence Length | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MHA-Abs | 137 K | 99.6 | 100.0 | 58.6 | 26.6 | 18.8 | 9.8 | 10.9 | 7.8 | |||||||
| MHA-RoPE | 137 K | 100.0 | 83.6 | 31.3 | 18.4 | 8.6 | 9.0 | 5.5 | ||||||||
| MHA-xPos | 137 K | 100.0 | 99.6 | 67.6 | 25.4 | 7.0 | 9.0 | 7.8 | ||||||||
| H3 | 153 K | 100.0 | 80.9 | 39.5 | 23.8 | 14.8 | 8.2 | 5.9 | 6.6 | 8.2 | 4.7 | 8.2 | 6.3 | 7.4 | ||
| Hyena | 97.7 | 100.0 | 44.1 | 12.5 | 6.6 | 5.1 | 7.0 | 5.9 | 6.6 | 6.6 | 5.9 | 6.3 | 9.8 | |||
| Mamba | 74 K | 100.0 |
- 대부분의 파라미터는 학습 가능한 positional encoding에 있다.
E Experimental Details and Additional Results
E. 1 Synthetic Tasks
Selective Copying
우리의 설정은 길이 4096의 시퀀스이며, 16개의 가능한 토큰(Figure 2의 흰색 "noise" 토큰 포함)으로 구성된 어휘 크기를 가진다. 모델은 16개의 "데이터" 토큰을 기억해야 한다. 우리는 모델 차원 인 2-layer 모델을 사용한다.
모델은 400K 스텝 동안 배치 크기 64, 상수 학습률 0.0001로 학습된다.
Induction Heads
학습은 매 스텝마다 무작위로 데이터를 생성하며, 배치 크기는 8이다. 우리는 "epoch" 크기를 8192 스텝으로 설정하고, 각 목표 시퀀스 길이별로 고정된 validation set(역시 무작위로 생성됨)에 대한 정확도를 추적한다.
MHA-Abs 및 Mamba 모델의 경우, 25번째 epoch (8192 × 25 = 204800 스텝) 이후의 결과를 보고한다.
MHA-RoPE 및 MHA-xPos 모델의 경우, 50번째 epoch (8192 × 50 = 409600 스텝) 이후의 결과를 보고한다.
LTI H3 및 Hyena 모델의 경우, 10번째 epoch (81920 스텝) 이후의 결과를 보고하는데, 이는 해당 시점에 이미 수렴하여 더 이상 성능 향상이 없었기 때문이다.
우리는 weight decay가 없는 Adam optimizer를 사용한다. 모든 모델은 상수 학습률 2e-4와 1e-3으로 학습되었으며, 각 모델에 대해 더 나은 결과가 보고된다 (Mamba를 제외한 모든 모델은 2e-4). Attention 및 Hyena 모델은 학습률 1e-3에서는 학습되지 않았다. H3는 두 학습률 모두에서 학습되었지만, 흥미롭게도 더 작은 학습률인 2e-4에서 더 짧은 시퀀스에 대해 더 나은 일반화 성능을 보였다. Mamba는 두 학습률 모두에서 학습되었지만, 더 큰 학습률인 1e-3에서 더 나은 extrapolation 성능을 보였다.
E. 2 Language Modeling
E.2.1 Scaling Law Details
Scaling law 실험은 일반적으로 GPT-3의 방식을 따랐다. 모든 모델은 GPT-2 tokenizer를 사용하여 The Pile 데이터셋으로 학습되었다.
모델 크기 (Model Sizes)
Table 12는 scaling law 실험에 사용된 모델 크기를 명시한다. 이 값들은 GPT-3의 사양(Brown et al. 2020)을 거의 그대로 가져왔으며, 아주 미미한 수정만 있었다.
첫째, 1.3B 모델의 batch size를 1M token에서 0.5M token으로 변경했는데, 이는 더 큰 batch size를 요구할 만큼 충분한 병렬화를 사용하지 않았기 때문이다.
둘째, 학습 token 수가 모델 크기에 비례하여 증가해야 한다는 Chinchilla scaling law (Hoffmann et al. 2022)에 맞추기 위해 학습 단계(training steps)와 총 token 수를 조정하였다.
학습 방식 (Training Recipes)
모든 모델은 AdamW optimizer를 사용했으며, 다음 설정을 따랐다:
- gradient clip value 1.0
- weight decay 0.1
- no dropout
- cosine decay가 적용된 linear learning rate warmup
기본적으로 peak learning rate는 GPT-3 사양을 따른다. 우리는 PaLM (Chowdhery et al. 2023) 및 LLaMa (Touvron et al. 2023)와 같은 인기 있는 대형 language model에서 채택된 변경 사항에서 영감을 받아 여러 모델에 "improved recipe"를 적용했다. 여기에는 다음이 포함된다:
- cosine decay가 적용된 linear learning rate warmup (최종 learning rate는 , peak value는 GPT-3 값의 5배)
- linear bias term 없음
- LayerNorm 대신 RMSNorm 사용
- AdamW hyperparameter (GPT-3 값) 사용 (PyTorch 기본값인 대신)
Table 12: (Scaling Law 모델 크기.) Scaling 실험을 위한 모델 크기 및 하이퍼파라미터. (모델 차원 및 헤드 수는 Transformer 모델에만 적용된다.)
| Params | n_layers | d_model | n_heads / d_head | Training steps | Learning Rate | Batch Size | Tokens |
|---|---|---|---|---|---|---|---|
| 125 M | 12 | 768 | 12 / 64 | 4800 | 6e-4 | 0.5 M tokens | 2.5 B |
| 350 M | 24 | 1024 | 16 / 64 | 13500 | 0.5 M tokens | 7B | |
| 760 M | 24 | 1536 | 16 / 96 | 29000 | 0.5 M tokens | 15 B | |
| 1.3 B | 24 | 2048 | 32 / 64 | 50000 | 0.5 M tokens | 26 B |
아키텍처 및 학습 세부 정보 (Architecture and Training Details)
우리의 모델은 다음과 같다:
- Transformer: GPT-3 (Table 12) 기반의 표준 Transformer이다.
- Transformer++: rotary positional encoding (Su et al. 2021) 및 SwiGLU MLP (Shazeer 2020)와 같은 개선된 아키텍처와 위에서 언급된 improved training recipe를 적용한 Transformer이다.
- Hyena: **Hyena block (S4가 MLP로 parameterized된 global convolution으로 대체된 H3 block)**과 표준 MLP block을 교차(interleave)하여 구성된다. MLP block은 확장 계수(expansion factor)가 4 대신 2이며, 파라미터 수를 보존하기 위해 layer 수가 1.5배 증가되었다.
- H3++: 몇 가지 수정 사항이 포함된 H3 아키텍처로, (i) 위에서 언급된 동일한 "thin" Hyena dimension 사용, (ii) 위에서 언급된 improved training recipe 적용, (iii) linear attention head dimension을 8로 설정하는 것을 포함한다.
- RWKV: B. Peng et al. (2023)의 기본 RWKV 모델이며, 수정된 MLP block을 포함한다. 또한 특정 파라미터에 대해 learning rate를 2배 또는 3배 증가시키는 등 명시된 학습 방식(training recipe)을 최대한 적용하였다.
- RetNet: Y. Sun et al. (2023)의 기본 RetNet 모델이다. 또한 위에서 언급된 improved training recipe를 적용하였다.
- Mamba: 표준 Mamba 아키텍처이며, improved training recipe를 적용하였다.
E.2.2 Additional Scaling Law Ablations
우리는 Figure 4 (왼쪽)의 2k context length scaling laws와 동일한 프로토콜을 사용하여 아키텍처에 대한 추가 ablation을 수행한다.
Mamba 아키텍처: 블록 인터리빙(Interleaving Blocks)
우리는 Mamba 블록과 결합된 다양한 아키텍처 블록의 효과를 테스트한다. 우리는 Mamba 블록이 단순히 표준 SwiGLU 블록에 추가적인 conv SSM 경로가 추가된 것이라는 관점에 초점을 맞춘다. 이는 두 가지 자연스러운 ablation으로 이어진다:
- Mamba 블록이 동질적으로 쌓이는 대신, 표준 MLP 블록과 인터리빙되면 어떨까? 이는 Mamba에서 SSM의 절반을 제거하는 것으로도 해석될 수 있다.
 Figure 9: (Scaling laws: 추가 ablation.) (왼쪽) 대신 (오른쪽) 대신
Figure 9: (Scaling laws: 추가 ablation.) (왼쪽) 대신 (오른쪽) 대신
- Mamba 블록이 MHA (multi-head attention) 블록과 인터리빙되면 어떨까? 이는 SwiGLU MLP를 가진 Transformer (즉, 우리가 Transformer++라고 부르는 것)에 단순히 SSM을 MLP 블록에 추가하는 것으로도 해석될 수 있다.
Figure 9 (오른쪽)은 이러한 변형들을 원래의 (동질적인) Mamba 아키텍처와 비교하여 보여준다. 흥미롭게도, 두 가지 변경 모두 큰 차이를 만들지 않는다. Mamba-MLP 아키텍처는 약간 더 나쁠 뿐이며, 여전히 Transformer++를 제외한 모든 모델보다 낫다. Mamba-MHA 아키텍처는 약간 더 좋을 뿐인데, 이는 최근 많은 연구에서 (LTI) SSM과 Attention을 결합하는 것이 상당한 개선으로 이어질 수 있다는 사실(Dao, Fu, Saab, et al. 2023; Fathi et al. 2023; Fathullah et al. 2023; Saon, Gupta, and Cui 2023; Zuo et al. 2022)을 고려할 때 다소 놀랍다.
H3 아키텍처: 학습 레시피(Training Recipes)
다음으로 우리는 Transformer++와 Mamba를 제외한 우리의 가장 약한 모델과 가장 강한 모델인 Hyena와 H3++ 간의 차이를 ablation하여, 특히 학습 레시피의 효과를 분리한다.
- Hyena: 원래 아키텍처와 GPT3 학습 레시피를 가진 Hyena 블록 (Figure 4와 동일).
- Hyena+: 동일한 아키텍처이지만 위에서 설명한 개선된 학습 레시피를 사용.
- H3+: Hyena+와 동일한 아키텍처이지만 Hyena convolution kernel을 S4D convolution kernel로 교체.
- H3++: H3+와 동일하지만 linear attention head dimension이 8. 이는 SSM recurrence 내부의 계산을 증가시키지만 파라미터 수는 증가시키지 않는다.
우리의 일반적인 관례는 "Model+"가 개선된 학습 레시피를 가진 기본 모델을 나타내고, "Model++"는 아키텍처 변경도 허용한다는 것이다.
Figure 9 (오른쪽)은 다음을 보여준다:
- 개선된 학습 레시피를 통해 큰 성능 향상이 이루어졌으며, 이는 주요 Figure 4의 많은 모델(RetNet, H3++, Transformer++, Mamba)에 사용되었다.
- 내부 LTI SSM의 선택은 중요하지 않다 (예: Hyena vs. S4). 이는 본 논문 전반의 결과와 일치한다.
- head dimension 확장이 성능을 향상시킨다. 이는 확장된 state dimension이 SSM의 성능을 향상시킨다는 우리의 주요 주제 중 하나(Section 3)와 일치한다.
E.2.3 Downstream Evaluation Details
이 사전학습 절차는 scaling law 프로토콜과 동일하지만, GPT2 tokenizer 대신 GPT-NeoX tokenizer (Black et al. 2022)를 사용하여 300B 토큰으로 확장되었다. 1.3B 모델의 경우, GPT3 사양과 일관성을 유지하기 위해 1M 토큰의 batch size를 사용한다. 우리는 Pile validation set에 대한 perplexity를 보고하며, 이 metric에 대해서는 동일한 데이터셋과 동일한 tokenizer로 학습된 모델, 특히 Pythia 및 RWKV와만 비교한다.
다운스트림 평가를 위해, 이 분야의 대부분의 연구에서와 같이 EleutherAI의 LM evaluation harness (L. Gao, Tow, et al. 2021)를 사용한다. 우리는 상식 추론(common sense reasoning)을 측정하는 다음 task/dataset에 대해 평가한다:
- LAMBADA (Paperno et al. 2016)
- HellaSwag (Zellers et al. 2019)
- PIQA (Bisk et al. 2020)
- ARC-challenge (P. Clark et al. 2018)
- ARC-easy: ARC-challenge의 쉬운 subset
- WinoGrande (Sakaguchi et al. 2021)
LAMBADA, WinoGrande, PIQA, ARC-easy에 대해서는 accuracy를 보고하며, HellaSwag 및 ARC-challenge에 대해서는 sequence length로 정규화된 accuracy를 보고한다 (이러한 task의 경우 거의 모든 모델에서 정규화된 accuracy가 더 높기 때문).
E. 3 DNA Modeling
E.3.1 Pretraining Details
우리는 HG38 사전학습 task의 데이터셋과 학습 절차에 대해 더 자세히 설명한다. 데이터셋은 이전 Enformer 유전체학 연구(Avsec et al. 2021)의 분할을 따른다. 학습 분할은 총 개의 길이 인 유전체 커버 세그먼트를 포함하며, 총 약 45억 개의 토큰(DNA 염기쌍)으로 구성된다. 이 세그먼트들은 (염색체 번호, 시작 인덱스, 끝 인덱스) 쌍으로 이루어져 있으며, 필요한 경우 (예: 더 긴 세그먼트를 얻기 위해) 확장될 수 있다.
학습 시퀀스 길이가 이 아닐 때 HyenaDNA와 차이가 발생한다. HyenaDNA는 항상 고정된 하위 세그먼트(예: 지정된 세그먼트의 시작 또는 중간)를 취하므로, 어떤 학습 시퀀스 길이에서도 각 epoch은 34021개의 샘플로 고정되며 전체 유전체를 반드시 통과하지는 않는다. 반면에 우리는 전체 학습 데이터를 사용한다:
- Context length 이 보다 작거나 같을 때, 각 세그먼트를 길이 의 겹치지 않는 하위 세그먼트로 나누어, 총 개의 샘플과 epoch당 개의 토큰이 되도록 한다.
- Context length 이 보다 클 때, 각 세그먼트를 두 개의 샘플로 변환한다. 하나는 지정된 세그먼트로 시작하고 다른 하나는 지정된 세그먼트로 끝난다. 따라서 각 epoch은 개의 항목과 epoch당 개의 토큰을 가진다. 예를 들어, 시퀀스 길이 에서는 기본값보다 4배 많은 토큰이 있고, 시퀀스 길이 에서는 16배 많은 토큰이 있다.
다른 학습 세부 사항은 일반적으로 우리의 language modeling 실험(Appendix E.2)과 동일한 프로토콜을 따른다. 예를 들어, 우리는 의 AdamW를 사용하고, dropout은 없으며, weight decay는 0.1이다. 총 단계의 10% 동안 linear warmup이 있는 cosine learning rate scheduler를 사용한다.
E.3.2 Scaling: Model Size Details
모델 (Models)
우리가 고려한 모델들은 다음과 같다:
- Transformer++: 개선된 아키텍처를 가진 Transformer로, 특히 RoPE positional encoding (Su et al. 2021)을 사용한다. 비공식적으로, 우리는 이 방식이 (Vaswani et al. 2017)의 바닐라 positional encoding보다 확연히 더 우수하다는 것을 발견했다.
- HyenaDNA: Nguyen, Poli, et al. (2023) 및 Poli et al. (2023)의 Hyena 모델로, 대략적으로 MHA 블록이 MLP로 parameterized된 global convolution을 사용하는 H3 블록으로 대체된 Transformer이다.
- Mamba: 표준 Mamba 아키텍처.
모델 크기 (Model Sizes)
우리는 다음 모델 크기를 사용한다.
| Blocks | 4 | 5 | 6 | 7 | 8 | 10 | 12 |
|---|---|---|---|---|---|---|---|
| Model Dimension | 64 | 96 | 128 | 192 | 256 | 384 | 512 |
| Params (Approx.) | 250 K | 700 K | 1.4 M | 3.5 M | 7.0 M | 19.3 M | 40.7 M |
Mamba의 블록 수는 두 배로 설정되었다는 점에 유의해야 한다. 이는 하나의 Transformer "layer"가 MHA와 MLP 블록을 모두 포함하는 반면 (Hyena도 유사), Mamba는 파라미터 수를 맞추기 위해 두 개의 Mamba 블록이 필요하기 때문이다 (Section 3.4).
학습 (Training)
각 모델 (Transformer++, HyenaDNA, Mamba)에 대해 학습률(learning rate)을 범위에서 탐색하였다.
최적의 Transformer 및 HyenaDNA 학습률은 모든 크기에서 ****이었다.
최적의 Mamba 학습률은 ****이었다. Mamba는 동일한 학습률()에서도 baseline보다 우수한 성능을 보였지만, 더 높은 학습률에서 더 안정적이고 성능이 더욱 향상되었다는 점에 주목해야 한다. (또한, 이 학습률이 탐색 범위의 상한에 가까웠으므로, 우리의 결과가 여전히 최적화되지 않았을 가능성도 있다.)
표준 LM scaling law (Table 12)와 달리, 우리는 단순화를 위해 모델 크기에 관계없이 학습률을 일정하게 유지했다. 최적의 학습률은 모델이 커질수록 낮아져야 하지만, 우리가 고려한 작은 모델 크기(최대 수백만 개의 파라미터)에서는 눈에 띄는 효과를 발견하지 못했다.
E.3.3 Scaling: Context Length Details
우리는 학습 단계당 총 배치 크기로 토큰을 사용하며, 이는 모든 시퀀스 길이에 적용된다 (예: 길이가 일 때는 배치당 16개의 세그먼트가, 길이가 일 때는 배치당 16384개의 세그먼트가 포함된다). 이는 일반적인 LM 표준에 비해 모델 크기 대비 큰 배치 크기이지만, 8개의 GPU와 의 시퀀스 길이를 가진 머신에서는 의 배치 크기가 최소 가능하며, HyenaDNA는 의 훨씬 더 큰 배치를 사용했다는 점에 주목해야 한다. 학습률은 Mamba의 경우 0.008, HyenaDNA의 경우 0.001을 사용했다. HyenaDNA의 경우 이전 섹션에서 사용했던 0.002의 동일한 학습률을 처음 시도했지만, 가장 긴 context 길이에서 불안정하다는 것을 발견했다.
Sequence Length Warmup. (Nguyen, Poli, et al. 2023)에 따라, 우리는 사전학습 중에 **sequence length warmup (SLW)**을 사용한다. 우리는 부터 시작하여 각 2의 거듭제곱 시퀀스 길이에서 2 epoch씩 진행하는 간단한 스케줄을 선택한다. (데이터가 큐레이션되는 방식 때문에, 가장 긴 시퀀스 길이에서는 비례적으로 더 많은 스텝과 토큰이 소모된다는 점에 유의하라. 특히, 길이 까지의 각 단계는 동일한 수의 토큰을 처리하지만, 길이 에서는 4배, 길이 에서는 8배, 길이 에서는 16배 더 많은 토큰이 처리된다.)
HyenaDNA와 달리, 우리는 항상 gradient 업데이트당 토큰 수를 제어하므로, 각 단계에서 시퀀스 길이가 두 배가 될 때마다 배치 크기는 연속적으로 절반으로 줄어든다.
Remark E.1. 우리는 또한 스케줄이 튜닝되지 않았으며, 이러한 사전학습 실험에서 sequence length warmup을 끄는 실험은 전혀 하지 않았다는 점에 주목한다. 우리는 나중에 SLW가 유사한 길이의 오디오 사전학습(Section 4.4)에는 눈에 띄게 도움이 되지 않는다는 것을 발견했으며, DNA 사전학습에도 필요하지 않을 가능성이 있다.
E.3.4 Species (Great Apes) Classification
모델은 **인과적(causal)**이므로, 모델 출력의 마지막 요소(시퀀스 길이 전체에 걸쳐)만 분류 head에 사용된다. 우리는 gradient step당 loss function에서 총 요소 수를 제어한다. 사전학습(pretraining) objective는 시퀀스 길이 전체의 모든 위치를 포함하여, batch_size sequence_length가 일정하게 유지된다. 즉, 시퀀스 길이가 증가함에 따라 batch size는 감소한다. 그러나 분류 task의 경우, 마지막 위치만 loss에 포함되므로 batch size 자체는 일정하게 유지된다. 이는 더 긴 시퀀스 길이로 모델을 fine-tuning하는 것이 더 많은 계산 비용을 수반한다는 의미이기도 하다.
학습은 10 epoch으로 구성되며, 각 epoch은 1024 gradient step을 가진다. 각 gradient step은 batch size 64를 사용하며, 이는 종(species)을 균일하게 선택하고, 염색체(chromosome)를 균일하게 선택한 다음, DNA의 연속적인 세그먼트를 균일하게 선택하여 독립적으로 무작위 추출된다.
(Nguyen, Poli, et al. 2023)에 따라, 최대 context length가 보다 큰 모델은 시퀀스 길이 warmup을 사용한다. 이는 길이에서 1 epoch, 길이에서 1 epoch, 길이에서 1 epoch 등으로 최대 시퀀스 길이까지 진행된다. 예를 들어, context를 가진 모델은 최대 시퀀스 길이에서 4 epoch을 더 진행하기 전에 6 epoch의 시퀀스 길이 warmup을 거친다.
모든 **Hyena 모델의 learning rate는 **이고, 모든 **Mamba 모델의 learning rate는 **이다. 이 값들은 더 작은 시퀀스 길이()에 대해 범위에서 각 모델별로 learning rate sweep을 수행하여 찾아졌다. 이 값들은 각 모델에 대해 일관되게 최적의 값으로 확인되었다. 길이에서는 축약된 learning rate sweep이 수행되었으며, 이 값들과 일치했다. 길이에서는 단일 실행이 수행되었다 (위에서 설명했듯이, 이러한 실험의 계산 비용은 시퀀스 길이에 비례한다). learning rate는 cosine decay schedule with warmup을 따랐으며, 최대 learning rate까지 5 epoch의 선형 warmup과 까지 5 epoch의 cosine decay로 구성되었다. 비정상적으로 긴 learning rate warmup schedule은 시퀀스 길이
Table 13: (Great Apes DNA Classification.) 동일한 context length의 사전학습된 모델을 사용하여 부터 길이의 시퀀스에 대해 fine-tuning한 후의 정확도(Accuracy). 무작위 추측은 20%이다.
| Model | Params | Accuracy (%) at Sequence Length | |||||
|---|---|---|---|---|---|---|---|
| HyenaDNA | 1.4 M | 28.04 | 28.43 | 41.17 | 42.22 | 31.10 | 54.87 |
| Mamba | 1.4 M | 31.47 | 27.50 | 27.66 | 40.72 | 42.41 | |
| Mamba | 7 M | 30.00 | 29.01 | 31.48 | 43.73 | 56.60 |
Table 14: YouTubeMix 길이 스케일링 시퀀스 길이 및 배치 크기.
| Sequence length | Batch size | Tokens / batch |
|---|---|---|
| 1 | 958464 | |
| 2 | 958464 | |
| 4 | 958464 | |
| 8 | 966656 | |
| 16 | 983040 | |
| 32 | 983040 | |
| 64 | 1048576 | |
| 128 | 1048576 |
warmup도 길었기 때문이다 (예: context를 가진 모델의 경우 10 epoch 중 6 epoch을 차지). 우리는 이 선택에 대해 추가 실험을 진행하지 않았다.
Species classification task의 결과는 Table 13에 있다.
E. 4 Audio Details
E.4.1 YouTubeMix Audio Pretraining
모델 (Model)
우리는 스테이지당 3개의 블록(총 15개의 Mamba 블록), 풀링 팩터 , 그리고 **외부 차원 **를 가진 모델을 사용하며, 이는 약 3.5M 파라미터에 해당한다.
데이터셋 (Dataset)
데이터는 8비트 mu-law 인코딩되어 있으며, 따라서 모델은 어휘 크기 256의 이산 토큰을 모델링한다.
데이터셋은 최대 1분 길이(960000 길이)의 클립으로 구성되며, 이는 서브샘플링되어 원하는 시퀀스 길이의 세그먼트로 나뉜다. 아키텍처가 16의 풀링 팩터를 가진 두 개의 스테이지를 포함하고, 하드웨어 효율성을 위해 결과 시퀀스 길이가 8의 배수가 되도록 하므로, **가장 긴 시퀀스는 **이다. 나머지 시퀀스 길이는 이를 연속적으로 절반으로 줄이고 가장 가까운 2048의 배수로 반올림하여 정의된다.
Table 14는 Figure 7에 사용된 사양을 나열한다. 다양한 배치 크기 외에도, 학습 세트의 유효 세그먼트 수가 다른 시퀀스 길이마다 달랐는데(예: 그래프의 다른 지점마다 epoch당 학습 단계 수가 일정하지 않았음), 이는 스케일링 곡선의 꺾임(kinks)에 기여했을 수 있다.
학습 (Training)
모델은 최대 학습률 0.002, 20K(10%) 웜업 단계, 그리고 0.1의 weight decay로 200K 학습 단계 동안 훈련되었다 (다양한 도메인에 걸친 우리의 일반적인 사전학습 방식과 유사).
추가 Ablation: SSM Parameterizations
우리는 Figure 7의 설정에서 long-form 오디오 waveform 사전학습에 대한 SSM parameterization을 조사한다. 설정은 더 큰 모델(8개 layer 및 6M 파라미터에 대해 , SaShiMi 기본값), 더 짧은 시퀀스(에서 까지, 에서 대신), 더 낮은 학습률(0.002에서 0.001), 그리고 **더 짧은 학습 주기(200K 단계 대신 100K 단계)**를 사용하도록 약간 수정되었다.
Figure 10은 **S4 S6로의 변경(즉, selection mechanism)**이 항상 유익한 것은 아님을 보여준다. long-form 오디오 waveform에서는 실제로 성능을 크게 저해하는데, 이는 오디오가 균일하게 샘플링되고 매우 부드러우며, 따라서 일치하는 inductive bias를 가진 연속 선형 시불변(LTI) 방법으로부터 이점을 얻는다는 관점에서 직관적일 수 있다. selection mechanism을 제거한 후, 결과 모델은 Mamba 블록 내부의 S4 layer임을 주목하라. 혼동을 피하기 위해, 우리는 이를 기본 Mamba 아키텍처인 Mamba-S6와 대조하여 Mamba-S4라고 부른다.
 Figure 10: (오디오 사전학습 (YouTubeMix) Ablation.) 균일하게 샘플링된 "연속" 신호 양식으로서, 오디오 waveform은 실제로 일치하는 inductive bias를 가진 LTI 모델로부터 이점을 얻는다. (왼쪽) 동질 모델 (모든 블록이 동일한 parameterization을 가짐) (오른쪽) 중앙 U-Net 블록만 ablation됨; 외부 블록은 Mamba-S4이다. 보라색 선은 왼쪽 그림과 동일하다.
Figure 10: (오디오 사전학습 (YouTubeMix) Ablation.) 균일하게 샘플링된 "연속" 신호 양식으로서, 오디오 waveform은 실제로 일치하는 inductive bias를 가진 LTI 모델로부터 이점을 얻는다. (왼쪽) 동질 모델 (모든 블록이 동일한 parameterization을 가짐) (오른쪽) 중앙 U-Net 블록만 ablation됨; 외부 블록은 Mamba-S4이다. 보라색 선은 왼쪽 그림과 동일하다.
그러나 오른쪽에서는 U-Net Mamba-S4의 외부 layer를 유지하고 내부 layer만 ablation한다. 성능 차이가 극적으로 줄어든다. 이는 원시 오디오 신호에 가까운 layer는 LTI여야 하지만, 일단 외부 layer에 의해 "토큰화"되고 압축되면 내부 layer는 더 이상 LTI일 필요가 없다는 가설을 강화한다. 그러나 이 설정에서도 실수 값 SSM은 복소수 값 SSM보다 여전히 성능이 떨어진다.
E.4.2 SC09 Speech Generation
Autoregressive 학습은 주로 다음과 같은 autoregressive language modeling 프로토콜을 따랐다:
- Weight decay 0.1
- 전체 스텝의 10%에 해당하는 learning rate warmup
- 를 사용하는 AdamW optimizer
- Gradient clip value 0.1
우리는 learning rate 0.002와 batch size 16으로 200,000 스텝을 학습시켰다.
Table 4의 대형 Mamba 모델은 stage당 15개의 layer를 가지며, outer dimension은 이고 pooling factor는 4이다. 이 데이터셋은 규모가 작아(학습은 100 epoch 진행됨) 이 대형 모델의 경우 BPB(Bits Per Byte) 또는 NLL(Negative Log-Likelihood)에서 상당한 overfitting이 발생했음을 확인했다. 그러나 생성된 샘플의 자동 평가 지표는 학습 내내 지속적으로 개선되었다.
Table 5의 아키텍처 ablation에 사용된 모든 모델은 stage당 8개의 layer를 가지며, outer dimension은 이고 pooling factor는 4이다.
S4+MLP 블록은 대략 개의 파라미터(MLP의 expansion factor 2)를 가진다.
Transformer 블록은 개의 파라미터(MLP의 expansion factor 1)를 가진다.
Mamba 블록은 일반적인 개의 파라미터를 가진다.
모든 모델은 대략 총 6M개의 파라미터를 가진다.
E. 5 Efficiency Benchmark
Scan Operation
우리는 A100 80GB PCIe GPU에서 측정된 selective SSM의 핵심 연산인 parallel scan(Section 3.3)을 convolution 및 attention과 비교한다.
이 비교에는 global-convolution 모델에서 convolutional kernel을 계산하는 비용이나, attention에서 QKV projection을 계산하는 비용과 같이 핵심 연산 외의 다른 연산 비용은 포함되지 않는다.
baseline으로, 우리는 PyTorch에서 kernel fusion이 없는 표준 parallel scan을 구현하였다. 이는 파라미터 를 HBM에 materialize해야 한다. 우리의 scan 구현은 discretization 단계와 parallel scan을 융합하여, 모든 대규모 파라미터를 HBM에 materialize하는 비용을 절감한다.
Table 15: (메모리 벤치마크.) Mamba의 메모리 사용량은 가장 최적화된 Transformer와 유사하다. 125M 모델 결과.
| Batch size | Transformer (w/ FlashAttention-2) | Mamba |
|---|---|---|
| 1 | 4.6 GB | 4.8 GB |
| 2 | 5.2 GB | 5.8 GB |
| 4 | 6.9 GB | 7.3 GB |
| 8 | 11.5 GB | 12.3 GB |
| 16 | 20.7 GB | 23.1 GB |
| 32 | 34.5 GB | 38.2 GB |
Convolution의 경우, 우리는 PyTorch의 표준 구현을 사용한다. 이 구현은 입력과 필터에 대해 FFT를 개별적으로 수행하고, 주파수 도메인에서 곱셈을 한 다음, 역 FFT를 수행하여 결과를 얻는다. 시퀀스 길이 에 대한 **이론적 복잡도는 **이다.
Attention의 경우, 우리는 인과 마스크(causal mask)가 적용된 FlashAttention-2 (Dao 2024)와 비교한다. 이는 우리가 아는 한 가장 빠른 구현이다. 인과 마스크가 적용된 FlashAttention-2는 인과 마스크가 없는 경우보다 약 1.7배 빠르다. 이는 attention 항목의 약 절반만 계산되기 때문이다. 우리는 batch size를 1로 설정하고, 시퀀스 길이를 부터 까지 증가시킨다 (일부 baseline은 500K에 도달하기 전에 메모리 부족이 발생한다). 모델 차원 , 상태 차원 을 사용한다. 대규모 학습에 가장 일반적으로 사용되는 데이터 타입인 BF16 입력을 사용하여 측정한다.
End-to-end Inference
우리는 Mamba 1.4B 모델과 학습되지 않은 Mamba 6.9B 모델의 추론 처리량을 표준 Transformer (GPT3 아키텍처) 1.3B 및 6.7B 모델과 비교한다. Transformer 구현은 Huggingface transformers 라이브러리의 표준 구현을 사용한다.
prompt 길이는 2048, 생성 길이는 128로 설정한다. batch size는 1, 2, 4, 8, 16, 32, 64, 128로 다양하게 변경하며, 128개의 토큰을 생성하는 데 걸리는 시간을 측정한다. 그 후 처리량(tokens/s)을 batch size 으로 계산한다. 측정은 3회 반복하여 평균값을 취한다. 측정은 A100 80GB PCIe GPU에서 수행된다.
Memory Benchmark
메모리 사용량은 대부분의 딥 시퀀스 모델과 마찬가지로 activation tensor의 크기에 비례하여 증가한다. 우리는 125M 모델의 학습 메모리 요구 사항을 1대의 A100 80GB GPU에서 측정하여 보고한다. 각 batch는 길이 2048의 시퀀스로 구성된다.
우리는 가장 메모리 효율적인 Transformer 구현(torch.compile의 kernel fusion 및 FlashAttention-2 포함)과 비교한다. Table 15는 Mamba의 메모리 요구 사항이 극도로 최적화된 구현을 가진 유사 크기의 Transformer와 비슷하며, 향후 Mamba의 메모리 사용량은 더욱 개선될 것으로 예상된다.