CLIPLoss와 Norm 기반 데이터 선택 방법을 통한 Multimodal Contrastive Learning
이 논문은 대규모 시각-언어 모델 사전학습 시 발생하는 노이즈가 많은 웹 데이터셋 문제를 해결하기 위한 두 가지 새로운 데이터 선택 방법을 제안합니다. 첫째, 기존 CLIPScore의 한계를 보완하기 위해 CLIP 학습 손실에서 영감을 받은 surrogate-CLIPLoss (s-CLIPLoss)를 도입하여, contrastive pair와의 유사도를 정규화 항으로 추가함으로써 데이터 품질을 더 정확하게 측정합니다. 둘째, 다운스트림 작업이 알려진 경우, 사전학습 데이터와 목표 데이터 간의 유사성을 측정하는 새로운 놈(norm) 기반 메트릭인 NormSim을 제안합니다. 이 방법들은 OpenAI의 CLIP-L/14 모델만을 사용한 기준선 대비 ImageNet-1k에서 5.3%, 38개 다운스트림 작업에서 평균 2.8%의 성능 향상을 보였으며, 기존 SOTA 방법과 결합하여 DataComp-medium 벤치마크에서 새로운 최고 성능을 달성했습니다. 논문 제목: CLIPLoss and Norm-Based Data Selection Methods for Multimodal Contrastive Learning
Wang, Yiping, et al. "Cliploss and norm-based data selection methods for multimodal contrastive learning." Advances in Neural Information Processing Systems 37 (2024): 15028-15069.
CLIPLoss and Norm-Based Data Selection Methods for Multimodal Contrastive Learning
Abstract
대규모 visual-language model 사전학습(예: CLIP)에서 데이터 선택은 특히 노이즈가 많은 웹 기반 데이터셋과 관련하여 핵심적인 문제로 부상했다. 주요 데이터 선택 접근 방식은 세 가지이다: (1) 외부 non-CLIP 모델을 활용하여 데이터 선택을 돕는 방법, (2) 원래 OpenAI CLIP 모델보다 고품질 데이터 선택에 더 효과적인 새로운 CLIP-style embedding 모델을 학습시키는 방법, (3) 특정 모델 속성을 요구하지 않고 어떤 CLIP embedding에도 보편적으로 적용 가능한 더 나은 metric 또는 전략을 설계하는 방법 (예: CLIPScore는 인기 있는 metric 중 하나).
첫 번째와 두 번째 접근 방식은 광범위하게 연구되었지만, 세 번째 접근 방식은 아직 충분히 탐구되지 않았다. 본 논문에서는 두 가지 새로운 방법을 제안하여 세 번째 접근 방식을 발전시킨다. 첫째, 단일 샘플에서 두 modality 간의 정렬(alignment)만을 고려하는 고전적인 CLIP score 대신, 우리는 surrogate-CLIPLoss를 소개한다. 이 방법은 CLIP 학습 loss에서 영감을 받아, 하나의 샘플과 그 contrastive 쌍 간의 정렬을 CLIPScore에 추가적인 정규화 항으로 더하여 품질 측정의 정확도를 높인다. 둘째, downstream task가 알려진 경우, 우리는 사전학습 데이터와 target 데이터 간의 유사성을 측정하기 위한 새로운 norm-based metric인 NormSim을 제안한다.
우리는 데이터 선택 벤치마크인 DataComp [1]에서 우리의 방법들을 테스트한다. OpenAI의 CLIP-L/14만을 사용하는 최고의 baseline과 비교했을 때, 우리의 방법들은 ImageNet-1k에서 5.3%의 성능 향상을, 38개 downstream 평가 task에서 2.8%의 성능 향상을 달성한다. 더욱이, sCLIPLoss와 NormSim 모두 기존 기술과 호환된다. 우리의 방법들을 현재 최고의 방법인 DFN [2] 및 HYPE [3]와 결합함으로써, downstream task의 평균 성능을 0.9% 향상시킬 수 있으며, DataComp-medium 벤치마크에서 새로운 state-of-the-art를 달성한다.
1 Introduction
웹에서 수집된 데이터로부터 대규모 visual-language 데이터셋을 큐레이션하는 것은 멀티모달 모델의 사전학습을 위해 일반적인 방법이 되었다. 그러나 이러한 웹 큐레이션 데이터 쌍의 품질은 여전히 중요한 병목 현상으로 남아있다. 연구에 따르면, 데이터셋의 선택은 모델과 학습 기술에 관계없이 모델 성능에 상당한 영향을 미친다 [4-11]. 이는 다양한 데이터 선택 전략 개발의 동기가 된다. 본 논문은 고정된 데이터 풀에서 subset을 최적화하여 zero-shot 다운스트림 task에서 우수한 성능을 달성하는 CLIP 모델 [4]을 학습하는 데 중점을 둔다.
고전적인 방법들은 오직 OpenAI(OAI)의 사전학습된 CLIP 모델(즉, teacher model)에만 의존하며 임베딩을 더 잘 활용하는 데 초점을 맞춘다. 가장 일반적으로 사용되는 방법은 CLIPScore를 계산하는 것으로, 이는 동일한 샘플에 대한 CLIP 모델의 시각 및 언어 임베딩 간의 코사인 유사도를 측정하여 텍스트와 이미지 간의 불일치가 있는 저품질 데이터를 제거한다. 다른 연구들은 이미지 기반 필터링 [1]과 같은 휴리스틱 분포 정렬 기술을 활용하여 다운스트림 task와 관련된 샘플을 선택하기도 한다. 이러한 접근 방식들은 일반적으로 제한적인 개선만을 제공하는 것으로 간주된다. 그러나 우리는 이러한 임베딩의 잠재력이 심각하게 저평가되었다고 주장한다. 본 연구는 OAI CLIP뿐만 아니라 다른 CLIP-스타일 모델에서도 주어진 임베딩을 더 잘 활용할 수 있는 보편적인 방법을 모색한다.
반면에, 최근의 선도적인 데이터 필터링 방법들은 임베딩 활용 전략 자체를 개선하는 데 초점을 맞추기보다는, 주로 외부 리소스를 활용하는 두 가지 다른 방향을 따른다. 이들은 (1) 데이터 선택을 돕는 외부 비-CLIP 모델을 사용하거나, (2) 외부 고품질 멀티모달 데이터를 사용하여 원래 OAI CLIP보다 더 나은 CLIP-스타일 임베딩 모델을 학습시켜 저품질 데이터를 필터링한다. 구체적으로, 첫 번째 연구 방향에서는 HYPE [3]가 고전적인 유클리드 기반 CLIP 대신 쌍곡선 모델의 임베딩을 활용하여 각 데이터 포인트가 다른 데이터 포인트와 얼마나 의미론적으로 겹치는지 측정하고 특이성이 낮은 데이터를 필터링한다. T-MARS [12]는 FAST [13]라는 상용 OCR 텍스트 감지 모델을 사용하여 캡션과 상관관계가 있는 유일한 feature가 텍스트인 이미지를 제거한다. Devil [14]은 fasttext [15]를 적용하여 비영어 텍스트를 제거하고 BLIP-2 [16] 모델을 사용하여 숫자 인식을 통해 숫자가 포함된 유용한 이미지를 유지한다. 두 번째 방향은 Data Filtering Network (DFN) [2]으로 대표되며, HQITP-350M과 같은 고품질 데이터셋을 사용하는 새로운 CLIP-스타일 teacher model을 학습시키는 것을 포함한다. 이 모델에서 추출된 임베딩은 다운스트림 task에서 OAI CLIP보다 성능이 떨어지지만, 저품질 데이터를 필터링하는 데 특히 우수하다. 주목할 점은 이러한 방법들 중 일부는 결합될 수 있으며, 실제로 DFN과 HYPE에서 선택된 데이터를 병합하면 HYPE [3]에서 보여주듯이 현재 state-of-the-art를 달성한다.
이전 연구들은 주로 CLIP 임베딩 품질을 개선하거나 외부 모델을 활용하여 필터링을 수행하는 데 중점을 두었지만, CLIPScore와 같은 고전적인 방법만을 사용하여 CLIP 임베딩을 최적화되지 않은 방식으로 활용했다. 이와 대조적으로, 본 연구에서는 주어진 CLIP 임베딩에 대한 필터링 방법 자체를 개선하는 데 초점을 맞춘다. 우리는 CLIP teacher model의 아키텍처(예: B/32 또는 L/14)나 학습된 데이터셋(예: OpenAI-WIT-400M 또는 DFN의 고품질 데이터셋)에 관계없이, 어떤 CLIP teacher model이든 활용할 수 있는 보편적이고 더 효과적인 전략이 있음을 보여준다. 이러한 전략은 DFN과 같은 새로 학습된 CLIP-스타일 모델의 사용과 항상 직교해야 하며, FAST 및 BLIP-2와 같은 외부 모델을 사용하는 방법과도 호환될 수 있다.
우리의 기여 (Our Contributions)
우리는 데이터 품질을 더 정확하게 특성화하는 surrogate-CLIPLoss라고 부르는 CLIPScore의 대안을 제안한다. 또한, 다운스트림 task에 대한 지식이 있을 때 **p-Norm Similarity Score (NormSim)**라고 부르는 새로운 분포 측정 지표를 도입한다. 두 가지 주요 관찰이 우리의 제안에 직접적인 영향을 미친다:
- 첫째, 우리는 고전적인 방법들이 시각 및 언어 임베딩 간의 코사인 유사도를 계산하여 멀티모달 샘플의 품질을 측정하며, 유사도가 낮을수록 텍스트가 이미지 부분과 잘 일치하지 않는다고 믿는다는 것을 관찰했다. 그러나 우리는 일부 정보가 적은 샘플들이 체계적인 편향을 가질 수 있으며, 이는 더 높은 CLIPScore로 이어진다는 것을 발견했다. 예를 들어, "image"라는 단어를 포함하는 언어 부분은 텍스트가 이미지 내용을 정확하게 설명하지 않더라도 어떤 시각 부분과도 더 높은 유사도를 보일 수 있다. 우리가 제안하는 s-CLIPLoss 방법은 표준 CLIP 학습 손실에서 영감을 받아, 샘플과 그 contrastive 쌍 간의 유사도로 원래 CLIPScore를 정규화한다. 예를 들어, "image"라는 단어로 인해 발생하는 높은 점수는 일반적으로 contrastive 쌍 전반에 걸쳐 일관되므로, 우리의 조정은 이러한 편향을 줄인다. 우리가 강조했듯이, 이러한 대체는 다양한 임베딩 모델에 보편적으로 적용될 수 있다. 그림 2에서 설명을 참조하라.
- 둘째, 대상 task와 동일한 분포에서 추출된 예시에 접근할 수 있다면, 이 추가 지식을 데이터 필터링 프로세스에 활용할 수 있다고 가정하는 것이 자연스럽다. 우리는 학습 샘플 와 대상 task 데이터셋 간의 시각 유사도를 측정하는 NormSim 지표를 제안한다. 이는 로 정의되며, 여기서 는 teacher model의 vision encoder이므로 , 그리고 이고, 는 norm이다. 효과적인 선택은 또는 이다. 특히, 학습 세트를 클러스터링하고 모든 대상 샘플에 대한 가장 가까운 이웃 그룹을 찾아 다운스트림 task만큼 학습 세트를 다양하게 유지하려는 이전의 ImageNet 기반 필터링 [1]과 달리, 우리의 방법은 다양성을 명시적으로 고려하지 않지만, 어떤 대상 샘플과도 가까운 예시를 선택한다(즉, 높은 NormSim 점수를 선택). 주목할 점은 s-CLIPLoss와 NormSim이 데이터 선택에서 상호 보완적인 효과를 누린다는 것이다. 그림 3을 참조하라.
우리의 방법의 효과를 설명하기 위해, 우리는 널리 사용되는 벤치마크 DataComp [1]을 데이터 필터링 방법으로 생성된 데이터셋을 평가하는 주요 방법으로 사용한다. 우리는 CLIPScore를 s-CLIPLoss로 단순히 대체하고 NormSim을 활용함으로써 ImageNet-1k에서 5.3%, 38개 다운스트림 task에서 평균 2.8%의 성능 향상을 달성할 수 있음을 보여준다. 이는 많은 외부 리소스 기반 방법들이 달성한 성능과 유사하거나 심지어 더 우수하다. 특히, 대상 다운스트림 task를 사용할 수 없는 경우에도, 학습 세트에서 구성된 프록시 다운스트림 task인 NormSim 를 s-CLIPLoss와 결합하여 사용하면 38개 다운스트림 평가에서 1.9%의 개선을 얻을 수 있다.
더욱이, 우리 방법으로 달성된 개선은 OAI CLIP 기반 방법에만 국한되지 않고, 외부 리소스를 필요로 하는 고급 모델과 결합하여도 얻을 수 있다. s-CLIPLoss와 NormSim으로 선택된 subset을 현재 state-of-the-art 방법인 "HYPE DFN"으로 선택된 subset과 병합함으로써, ImageNet-1k와 평균 38개 다운스트림 task 모두에서 0.9% 추가 개선을 달성할 수 있다. 또한, DFN과 우리의 전략으로 선택된 데이터만을 사용하여 "HYPE DFN"보다 평균 38개 task에서 0.8% 개선을 달성할 수 있다. 더 중요한 것은, CLIPScore의 대체품으로서 s-CLIPLoss가 OAI-L/14, OAI-B/32, DFN-B/32와 같은 다른 임베딩 모델에도 적용될 수 있으며, 평균 38개 task에서 0.4%에서 3.0%까지 보편적으로 성능을 향상시킨다는 것을 보여준다. 이 결과는 임베딩에서 사용 가능한 정보를 이해하는 데 기술적으로 통찰력을 제공할 뿐만 아니라 실질적으로도 중요하다. 기존 방법과 비교하여, 우리의 접근 방식은 Table 5에서 보여주듯이 재처리 및 새로운 임베딩 재학습 모두에서 상당한 양의 계산 시간을 절약한다.
2 Problem Setup
멀티모달 데이터셋의 데이터 필터링 (Data Filtering on Multimodal Dataset)
우리는 학습 데이터셋 이 주어졌다고 가정한다. 여기서 는 이미지-텍스트 (vision-language) 학습 쌍이다. 편의상, 우리는 상첨자 을 두 가지 양식(modality) 중 하나를 나타내는 데 사용할 것이며, 예를 들어 와 같이 표현한다. 우리의 목표는 CLIP 모델을 학습시키는 데 사용될 때, 특정 다운스트림 task에서 CLIP 모델의 zero-shot 정확도를 최대화하는 의 부분집합 을 식별하는 것이다.
CLIP score 및 embedding
LAION [5] 및 DataComp [1]과 같은 최근 연구들은 OpenAI의 CLIP ViT-L/14 모델 [4]을 teacher model로 사용하여 품질 점수를 얻는다. 여기서 우리는 이 vanilla CLIP 모델을 로 표기한다. 어떤 쌍 에 대해, 모델은 정규화된 단위 벡터 를 출력한다. 만약 이 개의 샘플을 포함하는 데이터셋을 나타낸다면, 우리는 를 embedding matrix로 정의한다. 널리 사용되는 필터링 지표인 "CLIPScore"는 로 정의된다.
데이터셋 및 모델 (Dataset and model)
여기서 우리는 DataComp [1]의 파이프라인을 따라 학습 및 평가 프로세스를 표준화한다. 이는 vanilla CLIP 모델을 오픈 소스화하고 더욱 개선하기 위한 데이터셋 실험의 테스트베드이며, 이전 데이터 선택 논문들 [17, 18, 12, 2, 19, 7]에서 널리 채택되었다. 자세한 내용은 Sec. 4에서 다룰 것이다.
3 Data Filtering Strategy
3.1 s-CLIPLoss: A Better Metric than CLIPScore
이 섹션에서는 기존의 일반적인 지표인 CLIPScore를 직접 대체하는, 더 우수하고 통계적으로 해석 가능한 품질 지표인 s-CLIPLoss를 소개한다. Figure 1은 s-CLIPLoss가 어떻게 작동하는지 보여준다. 이 새로운 지표는 무시할 수 있을 정도의 추가적인 계산 비용만 필요하며, 추가적인 외부 데이터 수집 비용은 전혀 들지 않는다. 이름에서 알 수 있듯이, 이 지표는 teacher CLIP 모델의 실제 학습 과정에서 사용되는 표준 CLIP loss에서 영감을 받았다. 이 loss는 다음과 같이 정의된다:
여기서 는 특정 학습 단계에서 -번째 샘플이 속하는 랜덤 배치이며, 는 학습 가능한 온도(temperature) 파라미터이다. 특히, teacher loss는 주로 **정규화 항 **에 의해 CLIPScore와 차이가 나며, 이는 다음과 같다:
 Figure 1: s-CLIPLoss의 설명. CLIPScore는 이미지-텍스트 쌍의 품질을 **과소평가(하단 왼쪽, 데이터 품질은 높지만 CLIPScore가 낮음(음수 CLIPScore는 높음))하거나 과대평가(하단 오른쪽, 데이터 품질은 낮지만 CLIPScore가 높음(음수 CLIPScore는 낮음))**할 수 있다. 그러나 이 문제는 단순히 정규화 항 을 포함함으로써 완화될 수 있다. s-CLIPLoss는 teacher 모델을 사용하여 학습 데이터에 대한 surrogate CLIP loss를 계산하고, 더 정확한 지표 역할을 한다. 여기서 "Bottom X%"는 **전체 데이터셋 내에서 하위 X%의 낮은 값(즉, 모든 값 중 X% 백분위수)**을 나타낸다. 예를 들어, ": Bottom "는 이 데이터가 전체 데이터셋 중에서 거의 가장 작은 값을 가지며, 이는 이미지와 텍스트 모두에서 매우 구체적인 요소들을 포함하고 있음을 의미한다. s-CLIPLoss에서 X 값이 낮을수록 데이터 품질이 높아야 한다.
Figure 1: s-CLIPLoss의 설명. CLIPScore는 이미지-텍스트 쌍의 품질을 **과소평가(하단 왼쪽, 데이터 품질은 높지만 CLIPScore가 낮음(음수 CLIPScore는 높음))하거나 과대평가(하단 오른쪽, 데이터 품질은 낮지만 CLIPScore가 높음(음수 CLIPScore는 낮음))**할 수 있다. 그러나 이 문제는 단순히 정규화 항 을 포함함으로써 완화될 수 있다. s-CLIPLoss는 teacher 모델을 사용하여 학습 데이터에 대한 surrogate CLIP loss를 계산하고, 더 정확한 지표 역할을 한다. 여기서 "Bottom X%"는 **전체 데이터셋 내에서 하위 X%의 낮은 값(즉, 모든 값 중 X% 백분위수)**을 나타낸다. 예를 들어, ": Bottom "는 이 데이터가 전체 데이터셋 중에서 거의 가장 작은 값을 가지며, 이는 이미지와 텍스트 모두에서 매우 구체적인 요소들을 포함하고 있음을 의미한다. s-CLIPLoss에서 X 값이 낮을수록 데이터 품질이 높아야 한다.
실제로, OAI-WIT400M [4]과 같은 teacher CLIP 모델의 학습 데이터셋과 실제 배치 분할 는 접근할 수 없으므로, 우리는 student 모델의 학습 데이터에서 개의 배치를 무작위로 선택하고, 의 평균 결과를 사용하여 에 대한 정규화 항 를 추정한다:
여기서 는 student 모델의 학습 데이터에서 무작위로 선택된 배치들이며, 이다. 우리는 실험에서 을 선택했지만, 5보다 큰 어떤 샘플 크기라도 원래 CLIPLoss를 추정하는 데 충분히 안정적이다 (자세한 내용은 Appendix D.1 참조). 또한, 에 의해 발생하는 계산 비용이 다른 baseline에 비해 무시할 수 있을 정도임을 보여준다 (Appendix C.1). 온도 와 배치 크기 는 사전학습된 teacher CLIP 모델의 파라미터에서 직접 얻을 수 있으므로, s-CLIPLoss는 CLIPScore에 비해 추가적인 파라미터를 도입하지 않는다. 의 집중 분석 (Appendix A.1), 의사 코드 (Algorithm 1), 및 의 ablation study (Appendix C.2)를 포함한 더 자세한 내용은 Appendix에 있다.
s-CLIPLoss의 동기
다른 기존 연구들도 NLP의 LESS [20], CV의 CoDis [21], 일반적인 데이터 스케줄링 시나리오의 RHO [22]와 같이 loss-guided 데이터 선택을 사용한다. 그러나 teacher loss 기반 선택이 멀티모달 contrastive learning에 적합한지는 여전히 불분명하다. Figure 2에서 볼 수 있듯이, s-CLIPLoss가 CLIPScore보다 일관되게 더 좋거나 동등한 성능을 보여주므로, 우리는 이에 대해 긍정적인 답변을 제시한다.
teacher loss가 우리의 선택에 어떻게 도움이 되는지 설명하기 위해, s-CLIPLoss가 제공하는 정규화 항이 CLIPScore에 내재된 과대평가 또는 과소평가를 수정하는 데 중요하다는 것을 보여준다. 높은 정규화 항은 이미지 임베딩, 텍스트 임베딩 또는 둘 다가 해당 대응 쌍을 넘어 여러 contrastive 쌍과 쉽게 일치할 수 있음을 의미한다. 예를 들어, Figure 1의 오른쪽 하단에서 "Image" 또는 "Photo"를 포함하는 텍스트는 어떤 시각적 콘텐츠와도 쉽게 일치할 수 있다. 유사하게, "verloopring" 이미지는 매우 단순한 feature만 포함하고 있어 "white", "empty", "circle" 등과 같은 많은 단어와 일치할 수 있다. 결과적으로, 더 낮은 음수 CLIPScore(높은 절대 CLIPScore)에도 불구하고, 배치 내의 상대적인 s-CLIPLoss는 더 높을 수 있다. 반대로, 왼쪽 하단은 "Islands Harbor", "American football", "sheep at green"과 같이 텍스트와 이미지 모두에서 매우 구체적인 요소들을 특징으로 한다. 이러한 요소들은 구체적이며 contrastive 쌍과 일치할 가능성이 적어, 상대적으로 낮은 s-CLIPLoss를 초래한다.
 Figure 2: DataComp-medium에서 s-CLIPLoss가 다양한 다운샘플링 비율에 걸쳐 CLIPScore보다 일관되게 우수한 성능을 보인다.
Figure 2: DataComp-medium에서 s-CLIPLoss가 다양한 다운샘플링 비율에 걸쳐 CLIPScore보다 일관되게 우수한 성능을 보인다.
 Figure 3: NormSim의 설명. 은 대상 사전 데이터이다. "Top X%"는 전체 데이터셋 내에서 상위 X%의 높은 값을 나타낸다. (a) 서로 다른 NormSim과 s-CLIPLoss를 가진 데이터의 시각화. 여기서는 (ImageNet-1k)를 예시로 사용한다. Type 2와 Type 4 데이터 모두 높은 s-CLIPLoss를 가지므로 품질이 높지만, 낮은 NormSim 를 가진 데이터(Type 4)는 ImageNet, VTAB, MSCOCO와 같은 다운스트림 task와 관련성이 더 낮다. 예를 들어, 이들은 OCR 콘텐츠가 지배적인 이미지를 많이 포함하고 있어 다운스트림 성능 향상에 거의 기여하지 않는다. (b) 다양한 필터링 방법에 대한 샘플링 데이터의 대략적인 비교 시각화. "s-CLIPLoss NormSim" 필터링을 사용하면 품질과 다운스트림 task 관련성 사이의 균형을 맞출 수 있어, Type 2 데이터의 비율을 높일 수 있다. (더 많은 시각화는 Appendix E를 참조하라.)
Figure 3: NormSim의 설명. 은 대상 사전 데이터이다. "Top X%"는 전체 데이터셋 내에서 상위 X%의 높은 값을 나타낸다. (a) 서로 다른 NormSim과 s-CLIPLoss를 가진 데이터의 시각화. 여기서는 (ImageNet-1k)를 예시로 사용한다. Type 2와 Type 4 데이터 모두 높은 s-CLIPLoss를 가지므로 품질이 높지만, 낮은 NormSim 를 가진 데이터(Type 4)는 ImageNet, VTAB, MSCOCO와 같은 다운스트림 task와 관련성이 더 낮다. 예를 들어, 이들은 OCR 콘텐츠가 지배적인 이미지를 많이 포함하고 있어 다운스트림 성능 향상에 거의 기여하지 않는다. (b) 다양한 필터링 방법에 대한 샘플링 데이터의 대략적인 비교 시각화. "s-CLIPLoss NormSim" 필터링을 사용하면 품질과 다운스트림 task 관련성 사이의 균형을 맞출 수 있어, Type 2 데이터의 비율을 높일 수 있다. (더 많은 시각화는 Appendix E를 참조하라.)
3.2 NormSim: A New Training-Target Similarity Metric
우리가 제안하는 s-CLIPLoss는 품질을 더 잘 추정하여 필터링 성능을 향상시키는 보편적인 접근 방식이며, 어떠한 다운스트림 task에도 의존하지 않는다.
이제, 만약 우리가 다운스트림 task에 대한 일부 지식에 접근할 수 있다면, vision-only -norm 유사도를 사용하여 각 학습 샘플과 다운스트림 타겟 데이터 간의 관계를 측정하는 타겟 데이터 metric을 통해 성능을 더욱 향상시킬 수 있다.
이 섹션 후반부에서 vision-only embedding을 사용하는 이유를 논의할 것이다.
구체적으로, 우리는 다운스트림 task의 타겟 세트에 접근할 수 있다고 가정하고 이를 으로 표기한다. 여기서 각 는 타겟 다운스트림 분포 에서 i.i.d. 샘플링되었지만, 테스트 세트와는 겹치지 않는다.
그러면, 각 학습 샘플 과 해당 타겟 세트 에 대해 NormSim은 다음과 같이 정의된다:
우리는 가장 높은 NormSim 점수를 가진 상위 개의 샘플을 선택하여 부분집합 를 구성한다. norm 유형 의 선택은 데이터 분포 및 학습 과정에 기반할 수 있다. 본 논문에서는 의 두 가지 인스턴스를 고려한다:
일 때, 우리의 데이터 선택 방법은 다음 방정식으로 간주될 수 있다. 이는 타겟 세트 분산의 주성분과 일치하는 부분집합을 선택하는 것과 동일하다 (Appendix C.6.1).
일 때, 거리 측정은 어떤 타겟 샘플과 높은 유사도를 가지면 학습 샘플이 선택되는, 더욱 낙관적인 측정으로 간주될 수 있다. 이는 이미지 기반 필터링 [1]에서 사용되는 nearest-neighbor 기반 방법과는 다르다. 해당 방법은 모든 타겟 샘플의 가장 가까운 학습 샘플을 찾으려고 시도한다. 이 경우, 다음과 같이 간주될 수 있다:
Appendix D.3에서는 우리의 NormSim가 다운스트림 타겟 task에서 nearest neighbor 선택보다 우수할 수 있음을 보여준다. 여기서는 Fig. 3에서 NormSim(ImageNet-1k)를 통해 선택된 예시를 보여주며, 이 vision-target-aware 방법이 품질 기반 방법과 상호 보완적임을 나타낸다.
타겟 데이터 선택 (Choice of Target Data). 실험 부분에서는 두 가지 종류의 타겟 데이터를 시도한다: ImageNet-1k (1.3M)의 학습 데이터 또는 접근 가능한 24개 다운스트림 task의 모든 학습 데이터 (2.1M). 우리는 이들을 각각 NormSim(IN-1k) 및 **NormSim(Target)**으로 표기한다.
Vision-only 정보 사용의 필요성 (Necessity of using vision-only information). 우리는 유사도를 측정하기 위해 멀티모달 정보 대신 시각 정보 만을 사용한다. 이는 일반적으로 크롤링된 텍스트가 간략한 캡션을 가지는 경우가 많아 OAI CLIP language embedding이 visual embedding 모델보다 약하기 때문이다 [1, 23-25]. 결과적으로, 언어 부분은 시각 부분만큼 사전학습 및 다운스트림 task 분포를 잘 특성화하지 못한다. 이러한 현상은 Gadre et al. [1]에서도 관찰되었는데, 이미지 기반 필터링(ImageNet-1k의 이미지 embedding과 유사한 데이터를 선택)이 텍스트 기반 필터링(ImageNet-21k의 단어를 포함하는 캡션을 가진 데이터를 선택)보다 우수한 성능을 보였다. 더 많은 ablation study는 Appendix D.4에 제공된다.
Teacher 모델 선택에서 NormSim의 일반성 (Generality of NormSim in choosing teacher model). 특히, 우리는 NormSim metric에서 이미지 embedding만을 사용하기 때문에, NormSim을 얻기 위해 CLIP 모델을 사용할 필요는 없다고 생각한다. NormSim은 사전학습된 ResNet-50에서 얻은 표현과 같이 좋은 이미지 표현이 주어진다면, 타겟 관련 이미지/이미지-텍스트 데이터를 선택하기 위한 일반적인 metric이 될 수 있다.
이론적 정당화 (Theoretical justification). 각 주변의 학습 샘플을 선택하여 다양성을 강제하는 기존의 많은 방법들과 달리, 우리의 전략은 데이터 다양성을 직접적으로 고려하지 않고 유사도를 최대화한다. 의 경우, NormSim를 최대화하는 것이 선형 모델 하에서 최적임을 Appendix A.2에서 보여준다. 우리의 정리는 또한 노이즈가 있는 embedding에 대한 오류 보장을 제공하며, vision-only embedding이 결합된 vision 및 language embedding보다 우수한 성능을 보이는 경우를 설명한다. Joshi et al. [26]의 최근 연구는 유사한 분석을 제공하지만, 고품질 데이터와 이미지 및 텍스트 간의 교차 분산에 중점을 둔다. 이 접근 방식은 위에서 논의한 바와 같이 노이즈가 있는 데이터셋을 필터링하는 데 이미지 전용 방법보다 덜 효과적이다.
다운스트림 에 접근할 수 없을 때 프록시 사용 (Using proxy when downstream is inaccessible). 놀랍게도, 우리는 사전학습 세트만 사용 가능할 때 2-norm도 사용될 수 있음을 보여준다. 이 경우, 우리는 사전학습 세트 자체에서 프록시 "타겟" 세트를 구성한다. 구체적으로, 를 단계에서 선택된 부분집합이라고 하면, 우리는 현재 를 프록시 "타겟" 세트로 간주한다. 다음으로 더 작은 세트를 구성하기 위해, 크기의 부분집합에 도달할 때까지 arg 를 만족하는 다음 데이터 배치 을 선택한다. 우리는 이 접근 방식을 **NormSim-D (Dynamic)**라고 부르며, 알고리즘 세부 사항은 Appendix C.3에서 설명할 것이다.
4 Experimental Results
이 섹션에서는 s-CLIPLoss와 NormSim의 성능을 평가하며, 다음 질문들에 답하고자 한다: Q1: 고정된 CLIP teacher 모델이 주어졌을 때, 우리의 방법이 CLIP embedding을 데이터 필터링에 더 효과적으로 활용할 수 있는가? Q2: 우리의 방법이 다양한 아키텍처나 다른 사전학습 데이터셋을 가진 CLIP teacher 모델에도 적용 가능한가? Q3: 우리의 방법이 외부 모델이나 멀티모달 데이터셋을 활용하는 다른 주요 접근 방식들과 비교했을 때 어떤가? 또한, 우리의 방법이 이러한 방법들과 호환되어 그 효과를 향상시킬 수 있는가?
4.1 Setup
우리는 DataComp 벤치마크 [1]의 표준화된 학습 및 평가 프로토콜을 따른다.
학습 설정 (Training configuration)
우리는 DataComp의 **중간 규모 학습 설정(DataComp-medium)**을 사용한다. 이 설정은 1억 2,800만 개의 저품질 웹 수집 이미지-텍스트 쌍으로 구성된 상당한 양의 데이터셋을 제공하며, 이 데이터는 필터링 과정을 거치게 된다.
특정 데이터 필터링 전략을 통해 데이터 subset이 얻어지면, 이 subset은 고정된 CLIP-B/32 모델을 학습시키는 데 사용된다. 학습 예산은 모델이 한 epoch당 1억 2,800만 개의 데이터 포인트를 처리할 수 있도록 설정되어 있다. 따라서, 더 작은 subset은 더 자주 반복되어 공정한 비교를 보장한다.
DataComp 데이터셋의 일부 이미지 URL이 유효하지 않게 되면서 시간이 지남에 따라 데이터셋의 크기가 작아진다는 점을 언급한다. 우리는 약 1억 1천만 개의 데이터만 성공적으로 다운로드했다. 따라서, 리더보드의 baseline 결과는 우리의 데이터셋에 직접 적용되지 않으므로, 우리는 리더보드의 모든 상위 baseline을 그들의 공개된 UID(선택된 데이터의 고유 식별자)를 사용하여 재현하였다.
평가 (Evaluation)
우리는 DataComp에서 제시한 대로 이미지 분류 및 검색 task를 포함한 38개의 다운스트림 데이터셋에서 모델 성능을 측정했다.
이미지 분류 task에는 ImageNet-1k [27], ImageNet distribution shifts [28-31], Visual Task Adaptation Benchmark (VTAB) [32]의 11개 데이터셋, 그리고 WILDS [33, 34]의 3개 데이터셋이 포함된다.
검색 데이터셋에는 **Flickr30k [35], MSCOCO [36], WinoGAViL [37]**이 포함된다.
Teacher model 아키텍처 (Teacher model architecture)
우리의 실험에서는 OpenAI의 CLIP teacher model로 ViT-L/14와 ViT-B/32 두 가지 아키텍처를 활용한다.
또한, Fang et al. [2]이 제안한 DFN (DFN-P)의 공개 버전을 teacher model로 사용하며, 이 모델의 아키텍처 역시 ViT-B/32이다.
4.2 Baselines
우리는 외부 자원 활용 정도에 따라 이전에 언급된 세 가지 현재 연구 방향을 다시 정의한다: (D1) OAI CLIP만을 사용하면서 embedding 활용 전략을 최적화하는 방향, (D2) 외부 데이터를 기반으로 더 발전된 CLIP embedding 모델을 훈련하고 사용하는 방향, (D3) CLIP이 아닌 외부 모델을 활용하여 데이터 선택을 돕는 방향. D2와 D3는 D1의 전략을 포함할 수도 있다는 점이 중요하다. 예를 들어, CLIPScore (D1)는 거의 모든 상위 방법에서 사용되었다. 따라서 우리는 가장 큰 범주를 포괄하는 기준으로 baseline을 분류한다. 위 분류에 따라, 실험에서 사용된 baseline들을 다음과 같이 요약한다. 자세한 내용은 Fig. 4와 Appendix C.4를 참조하라.
D1: OAI CLIP embedding만 사용. 학습자는 사전학습 데이터셋(예: DataComp-medium), embedding 추출에 사용되는 원본 OAI CLIP teacher model, 그리고 사전학습 데이터셋보다 훨씬 작은 다운스트림 task의 타겟 데이터(예: ImageNet-1k)에만 접근할 수 있다. 이 범주에서는 기존의 외부 non-CLIP 모델이나 외부 멀티모달 데이터셋을 기반으로 새로 훈련된 CLIP 모델을 사용하지 않는다. 구체적으로 이 범주에는 다음이 포함된다: (1) CLIPScore [38]: 이전에 언급했듯이, CLIPScore만을 필터링에 사용한다. (2) Image-based filtering [1]: ImageNet-1K 훈련 데이터를 데이터 필터링을 위한 다운스트림 타겟 데이터로 사용한다. 훈련 데이터의 이미지 embedding에 k-means clustering을 적용하고, ImageNet-1K embedding에 가장 가까운 클러스터를 선택한다. Gadre et al. [1]은 image-based filtering과 CLIPScore를 결합하는 시도도 한다. (3) Pruning [18]: 데이터셋을 무방향 그래프로 표현하고, 난이도(difficulty)와 다양성(diversity)을 결합하여 데이터를 선택한다. 이들은 CLIP score를 사용하여 그래프를 초기화한다.
D2, D3: 접근 가능한 외부 모델 및 멀티모달 데이터. 현재 모든 상위 baseline들은 학습자가 외부 자원을 활용할 수 있도록 한다. 이는 더 나은 CLIP teacher model을 훈련하거나, 기존 모델의 속성을 사용하여 필터링을 돕는 방식이다. 구체적으로 다음이 포함된다: (1) DFN [2]: 외부 고품질 데이터를 통해 또 다른 CLIP 데이터 필터링 네트워크를 훈련한다. 현재 공개된 모델(DFN-P)은 CC12M [39] + CC3M [40] + SS15M [41]으로 훈련되었으며, 최고의 DFN은 비공개 HQITP-350M [2]으로 훈련되었는데, 이는 DataComp-medium보다도 크다. (2) HYPE [3]: hyperbolic embedding (CLIP embedding과 다름)과 entailment cone 개념을 활용하여 의미 없거나 불충분하게 명시된 샘플을 필터링하고, 각 샘플의 특이성(specificity)을 향상시킨다. (3) HYPE DFN: [3]에서 제안된 방법으로, 각 방법에 대해 부분집합을 개별적으로 샘플링한 후 병합한다. 이는 DataComp 벤치마크의 medium 사이즈에서 state-of-the-art 방법이다. (4) **T-MARS [12], Devils [14], MLM [42]**를 포함한 다른 방법들: 텍스트 감지 모델 FAST [13], BLIP-2 [16], LLaVA-1.5 [43, 44]와 같은 외부 모델을 활용하여 데이터를 휴리스틱하게 선택한다. 자세한 내용은 Appendix C.4를 참조하라.
교차 설정 비교 (Cross-setting comparison). 우리는 공정한 비교를 위해 이러한 구분을 한다. 직관적으로 성능은 D2, D3 > D1 순으로 순위가 매겨져야 한다. 그러나 우리의 결과는 교차 설정 비교가 가능하며, 우리의 D1 방법들이 대부분의 D3 방법들과 유사하거나 심지어 더 나은 성능을 보일 수 있음을 보여준다.
Table 1: OpenAI의 CLIP-L/14 모델만 사용하는 방법들(D1 범주)의 DataComp-medium 결과. "dataset size"는 다양한 접근 방식으로부터 얻은 부분집합의 크기를 나타낸다. NormSim(IN-1k)는 ImageNet-1k의 훈련 데이터를 타겟으로 사용하는 것을 의미하며, NormSim(Target)은 사용 가능한 24개 다운스트림 task 전체의 훈련 데이터를 타겟으로 사용하는 것을 나타낸다. NormSim-D는 훈련 세트에서 반복적으로 선택된 부분집합을 타겟 프록시로 사용하는 방법들을 의미한다. 모호성을 피하기 위해, CLIPScore는 더 높은 값을 가진 데이터를 선택하는 반면, s-CLIPLoss는 더 낮은 값을 가진 데이터를 선택한다고 명시한다.
| Filtering Strategy | Dataset Size | IN-1k (1 task) | IN Dist. Shift (5) | VTAB (11) | Retrieval (3) | Avg. (38) |
|---|---|---|---|---|---|---|
| No filtering [1] | 110M | 17.3 | 15.0 | 25.2 | 21.3 | 25.6 |
| CLIPScore (20%) [38] | 22 M | 25.4 | 22.7 | 31.8 | 22.0 | 31.0 |
| CLIPScore (30%) [38] | 33M | 26.4 | 23.6 | 32.6 | 24.5 | 32.2 |
| Image-based [1] | 24 M | 25.5 | 21.9 | 30.4 | 24.6 | 29.9 |
| CLIPScore (30%) Image-based [1] | 11M | 27.4 | 23.9 | 31.9 | 21.4 | 30.8 |
| Pruning [18] | 22 M | 23.2 | 20.4 | 31.4 | 18.7 | 29.5 |
| s-CLIPLoss (20%) | 22 M | 27.4 | 23.8 | 33.7 | 23.7 | 32.5 |
| s-CLIPLoss (30%) | 33 M | 27.9 | 24.6 | 33.2 | 25.1 | 32.9 |
| CLIPScore (30%) NormSim -D | 22 M | 28.3 | 25.0 | 34.5 | 22.7 | 32.9 |
| s-CLIPLoss (30%) -D | 22 M | 29.8 | 26.1 | 34.8 | 24.6 | 34.1 |
| CLIPScore (30%) (IN-1k) | 22 M | 29.1 | 25.4 | 24.1 | 33.4 | |
| CLIPScore (30%) (Target) | 22 M | 28.9 | 25.1 | 32.7 | 23.6 | 32.5 |
| CLIPScore (30%) NormSim (IN-1k) | 22 M | 29.7 | 25.9 | 33.7 | 24.1 | 33.7 |
| CLIPScore (30%) NormSim (Target) | 22 M | 30.2 | 26.2 | 35.0 | 23.4 | 33.9 |
| s-CLIPLoss (30%) (IN-1k) | 22 M | 30.4 | 26.4 | 35.4 | 34.3 | |
| s-CLIPLoss (30%) (Target) | 22M | 30.6 | 26.2 | 35.2 | 25.5 | 33.9 |
| s-CLIPLoss IN-1k | 22 M | 31.9 | 27.3 | 34.8 | 25.0 | |
| s-CLIPLoss (30%) Target | 22 M | 31.7 | 27.2 | 36.0 | 26.0 | 35.0 |
4.3 Main Results and Discussions
4.3.1 Comparision on D1 Category (Q1)
Table 1에서 우리는 OAI CLIP 모델만 사용이 허용된 D1 방법들을 비교한다. 우리의 방법들은 OAI CLIP-L/14를 더 잘 활용한다. 첫째, s-CLIPLoss는 단독으로 사용되든 다른 방법들과 결합되든 모든 metric에서 CLIPScore를 능가한다. 이러한 결과는 s-CLIPLoss가 데이터 품질을 더 정확하게 추정할 수 있다는 우리의 주장을 뒷받침한다. 둘째, target knowledge를 사용할 수 없는 경우에도, NormSim -D를 s-CLIPLoss와 함께 사용하면 38개 다운스트림 task에서 평균 1.9%의 필터링 성능 향상을 가져올 수 있다. 셋째, target knowledge를 사용할 수 있는 경우, NormSim 와 NormSim 는 NormSim -D에 비해 필터링 성능을 더 크게 향상시키며, 일반적으로 NormSim 가 최적의 선택이다. 특히, 최고 baseline인 'CLIPScore (30%)'와 비교했을 때, 우리의 최고 조합인 's-CLIPLoss NormSim (Target)'는 ImageNet-1k에서 5.3%, 38개 다운스트림 task에서 평균 2.8%의 성능 향상을 보인다. Table 3에서 우리는 이 결과가 DFN HYPE를 제외한 모든 D3 baseline을 능가함을 확인할 것이다. 반면, ImageNet-1k를 target data로 사용할 때는 norm의 선택이 미치는 영향이 매우 적다.
Table 2: s-CLIPLoss는 다양한 CLIP teacher 모델에 적용될 수 있다. 우리는 OpenAI의 CLIP-B/32 모델 또는 DFN의 공개 버전(DFN-P)만을 사용한 DataComp-medium 결과를 보여준다. "NormSim "는 OAI CLIP-B/32를 사용하여 NormSim 를 계산하는 것을 나타낸다.
| Strategy | Size | IN-1k | VTAB | Avg. |
|---|---|---|---|---|
| OAI CLIP-B/32 | ||||
| CLIPScore (30%) | 33M | 27.6 | 33.6 | 33.2 |
| CLIPScore (20%) | 22 M | 27.0 | 33.0 | 32.2 |
| s-CLIPLoss (30%) | 33M | 28.8 | 33.7 | 33.6 |
| s-CLIPLoss (20%) | 22 M | 28.9 | 34.3 | 33.0 |
| s-CLIPLoss (30%) NormSim (Target) | 22 M | 32.4 | 35.9 | 35.2 |
| DFN-P | ||||
| CLIPScore (30%) | 33M | 28.4 | 33.2 | 32.7 |
| CLIPScore (20%) | 22 M | 29.7 | 33.0 | 33.1 |
| CLIPScore (17.5%) | 19 M | 30.2 | 34.1 | 33.8 |
| CLIPScore (15%) | 16M | 25.9 | 32.9 | 31.6 |
| s-CLIPLoss (30%) | 33M | 28.9 | 33.4 | 33.2 |
| s-CLIPLoss (20%) | 22 M | 30.7 | 33.6 | 33.8 |
| s-CLIPLoss (17.5%) | 19M | 31.2 | 35.7 | |
| s-CLIPLoss (15%) | 16M | 31.3 | 34.6 | |
| s-CLIPLoss (30%) NormSim (Target) | 22 M | 29.4 | 33.5 | 32.5 |
| s-CLIPLoss (17.5%) NormSim (Target) | 16M | 31.5 | 34.6 | 34.4 |
| s-CLIPLoss (17.5%) NormSim (Target) | 16M | 31.6 | 37.2 | 35.7 |
Table 3: DataComp-medium에서 모든 D1&D2&D3 최고 방법들의 결과. MLM [42]의 결과는 해당 논문에서 가져왔으며, 다른 모든 baseline은 공식 UID를 사용하여 다운로드한 데이터셋에서 재현되었다. "Ours (20%)"는 "s-CLIPLoss (30%) NormSim (Target)"을 사용하여 원본 데이터의 20%를 얻는 것을 의미하며, "Ours (10%)"는 "s-CLIPLoss (20%) NormSim (Target)"을 적용하여 10%를 얻는 것을 나타낸다. 그리고 우리는 "*"를 사용하여 OAI CLIP-B/32와 OAI CLIP-L/14를 각각 사용하여 선택된 데이터의 교집합을 선택한 경우를 나타내며, 이로 인해 "Ours (20%)"의 경우 약 15M 데이터, "Ours (10%)"의 경우 7.4M 데이터가 생성된다.
| Type | Filtering Strategy | Dataset Size | IN-1k (1) | IN Dist. Shift (5) | VTAB (11) | Retrieval (3) | Avg. (38) |
|---|---|---|---|---|---|---|---|
| D3 | T-MARS [12] | 22 M | 30.8 | 26.3 | 34.8 | 25.4 | 34.1 |
| D3 | Devil [14] | 20M | 31.0 | 26.7 | 35.9 | 24.7 | 34.5 |
| D3 | MLM [42] | 38M | 30.3 | 25.6 | 36.0 | 29.0 | 34.5 |
| D3 | HYPE [3] | 10 M | 30.3 | 25.8 | 34.3 | 22.2 | 31.9 |
| D2 | DFN [2] | 16M | 36.0 | 30.1 | 36.2 | 27.0 | 35.4 |
| D3 | DFN HYPE [3] | 20 M | 30.8 | 38.5 | 28.0 | 36.8 | |
| D1 | Ours (20%) | 22 M | 32.4 | 27.4 | 35.9 | 26.3 | 35.2 |
| D3 | DFN Ours (20%)* | 23 M | 38.6 | ||||
| D3 | DFN HYPE Ours (10%)* | 22 M | 37.3 | 31.4 | 27.6 | 37.7 |
4.3.2 Try Other Teacher Models (Q2)
우리의 방법이 다른 CLIP teacher model에도 적용되는지 평가하기 위해, 우리는 OAI CLIP-L/14를 OAI CLIP-B/32 및 DFN-P로 대체하여 embedding model로 사용했다. 우리는 최고 baseline인 "CLIPScore"와 우리의 "s-CLIPLoss" 및 최고 전략인 "s-CLIPLoss NormSim (Target)"을 비교했으며, 이는 Table 2와 Appendix D.2에 제시되어 있다.
원래 DFN 논문은 1,920만 개의 데이터 포인트로 구성된 subset을 선택했는데, 이는 우리 데이터셋의 약 17.5%이자 그들 데이터셋의 15%에 해당한다. 우리는 이러한 샘플링 비율을 비교에 반영했다.
s-CLIPLoss는 다양한 CLIP embedding model에 적용될 수 있다. 우리가 제안한 s-CLIPLoss는 CLIPScore를 대체하는 것으로, Table 1에서 보듯이 OAI CLIP-L/14를 사용한 다른 모든 baseline보다 더 나은 성능을 보일 뿐만 아니라, Table 2에서 보듯이 다른 두 CLIP embedding model인 OAI CLIP-B/32 및 DFN-P에서도 보편적인 성능 향상을 달성한다. 우리의 방법은 다양한 필터링 비율과 모델에 대해 모든 다운스트림 task에서 일관되게 우수한 성능을 보이며, 예를 들어 ImageNet-1k에서는 0.5%~5.4%의 성능 향상을 가져온다.
NormSim에 필요한 embedding은 좋은 다운스트림 성능을 가져야 한다. s-CLIPLoss와 NormSim 를 결합할 때, OAI CLIP-B/32와 DFN-P는 완전히 다른 행동을 보인다. 전자는 Table 1에서 OAI CLIP-L/14를 teacher model로 사용했을 때보다 더 좋은 결과를 얻는 반면, 후자는 s-CLIPLoss만 사용했을 때보다도 더 나쁜 결과를 얻는다. 그 이유는 DFN-P가 OAI CLIP-B/32와 달리, 저자들이 주장했듯이 다운스트림 task 성능을 희생하면서 데이터 필터링을 위해 특별히 설계되었기 때문이다. 예를 들어, DFN-P, OAI CLIP-B/32, OAI CLIP-L/14의 ImageNet-1k 정확도는 각각 45%, 63%, 75%이다. 이는 DFN에서 얻은 target 데이터의 embedding이 매우 신뢰할 수 없어서, 학습 데이터와 target 데이터 간의 유사도 계산이 부정확할 수 있음을 나타낸다. 이를 뒷받침하기 위해, "s-CLIPLoss (17.5%) NormSim (Target)"에서 보듯이, DFN-P를 사용하여 s-CLIPLoss를 평가하되, NormSim 계산에는 OAI CLIP-B/32를 활용하면, s-CLIPLoss만 사용했을 때보다 결과를 더욱 향상시킬 수 있다. Table 3에서 보듯이, 38개 task에 대한 평균 성능은 CLIPScore와 함께 최고의 DFN(HQITP-350M으로 학습)을 활용하는 것보다도 높다.
4.3.3 Comparison with D2 & D3 Categories (Q3)
이 부분에서는 Sec. 4.2에서 언급된 모든 D2 및 D3 baseline과 우리의 최적 전략을 Table 3에서 함께 비교한다. 공식 UID가 사용 가능한 모든 baseline은 여기서 재현하였다. Table 3에서 언급된 "A B"의 경우, Kim et al. [3]의 "HYPE DFN" 방식을 따라 데이터를 병합하였다. 이 방식은 각 방법에 대해 샘플링 subset을 개별적으로 생성한 후 이를 병합하는 것으로, 공유되는 데이터가 중복 샘플링될 수 있으며, 이는 직관적으로 더 중요하다고 판단된다. 우리는 또한 Table 4에서 DataComp-medium 전체 데이터셋에 대해 우리의 방법을 DFN [2] 및 HYPE [3]와 결합하여 얻은 최상의 결과를 보여준다. 여기서 baseline은 DataComp 벤치마크에서 가져온 것이다.
우리의 방법은 대부분의 D3 방법을 능가할 수 있다. Table 3에서 우리는 어떠한 외부 모델이나 데이터도 사용하지 않고, 우리의 최적 조합인 "s-CLIPLoss NormSim (Target)" (Ours (20%))이 DFN과 "DFN HYPE"를 제외한 모든 방법을 여전히 능가함을 보여준다. 이는 Q3의 첫 번째 부분에 대한 답변이며, CLIP embedding이 이미 필요한 정보를 포함하고 있으므로 일부 외부 모델이 불필요할 수 있음을 추가로 시사한다.
우리는 SOTA 방법을 더욱 개선할 수 있다. Table 3에서 우리는 우리의 모델이 현재 SOTA 방법인 "HYPE DFN"의 성능을 ImageNet-1k에서 0.9%, 평균 38개 다운스트림 task에서 0.9% 향상시킬 수 있음을 보여준다. 외부 embedding 모델 MERU [45]를 활용하는 HYPE를 결합하지 않고도 유사한 결과를 얻을 수 있다. 그리고 Table 4에서 보여주듯이 DataComp-medium (전체 데이터셋) 벤치마크의 SOTA 성능을 업데이트하였다. 여기서 우리는 OAI CLIP-B/32와 L/14 모두에 의해 선택된 데이터를 사용했는데, 이는 둘 중 하나만 사용하는 것보다 더 견고하다는 것을 발견했다. 우리의 더 나은 결과는 Q3의 두 번째 부분, 즉 우리의 방법이 다른 D2 및 D3 방법과 호환될 수 있다는 질문에 답한다.
Table 4: 우리의 방법을 전체 DataComp-medium 데이터셋 (128M 데이터)에 적용한 후, 새로운 state-of-the-art 결과를 달성하였다. 더 자세한 내용은 DataComp 벤치마크에 있다.
| Strategy | IN-1k | Avg. |
|---|---|---|
| No filtering | 17.6 | 25.8 |
| CLIPScore [38] | 27.3 | 32.8 |
| T-MARS [12] | 33.0 | 36.1 |
| Devils [14] | 32.0 | 37.1 |
| DFN [2] | 37.1 | 37.3 |
| DFN HYPE [3] | 37.9 | |
| DFN Ours | ||
| DFN HYPE Ours |
5 Conclusion and Limitation
본 논문에서는 외부 리소스에 의존하지 않고 멀티모달 contrastive learning에서 데이터 선택을 향상시키기 위해 두 가지 metric인 s-CLIPLoss와 NormSim을 소개한다. s-CLIPLoss는 일반적으로 사용되는 CLIPScore에 비해 더 정확한 품질 metric을 제공하며, NormSim은 사전학습 데이터와 알려진 다운스트림 task를 위한 타겟 데이터 간의 유사성을 측정한다. 실험 결과, 우리의 방법은 외부 모델이나 데이터셋을 사용하는 접근 방식과 비교하여 경쟁력 있거나 심지어 더 나은 결과를 달성한다. 또한, s-CLIPLoss와 NormSim은 기존의 최고 기술들과 호환되어, 이들을 결합함으로써 새로운 state-of-the-art를 달성할 수 있다.
본 연구의 주목할 만한 한계점은 DataComp의 large 및 xlarge 스케일과 같은 더 큰 사전학습 데이터셋을 제외했다는 점이다. 그러나 DataComp-medium은 CLIP 사전학습에서 데이터 선택을 위한 가장 일반적으로 사용되는 벤치마크이며, 우리의 방법은 이 벤치마크에서 효과성(Table 1, 3)과 효율성(Table 5)을 모두 입증했다. 향후 연구 방향으로는 서로 다른 방법으로 선택된 데이터를 병합하는 더 나은 방법을 탐색하고, 데이터 스케줄링 시나리오에 우리의 방법을 통합하는 것을 포함한다.
6 Acknowledgement
Tong Chen, Pang Wei Koh, Xiaochuang Han, Rui Xin, Luyao Ma, Lei Chen 및 UW ML Group의 다른 구성원들에게 통찰력 있는 토론과 유익한 피드백에 감사드린다. Kevin Jamieson과 Yifang Chen의 연구는 University of Washington Materials Research Science and Engineering Center, DMR-2308979 및 CCF 2007036을 통해 NSF의 부분적인 지원을 받았다. SSD는 NSF IIS 2110170, NSF DMS 2134106, NSF CCF 2212261, NSF IIS 2143493, NSF CCF 2019844 및 NSF IIS 2229881의 지원에 감사드린다.
A Theoretical Interpretation
A. 1 Concentration of Normalization Term in s-CLIPLoss
이 섹션에서는 concentration inequality를 사용하여 batch size가 충분히 클 때, 실제 batch 에서 얻은 정규화 항(normalization term) 가 ground truth batch 를 사용하여 계산된 를 상당히 잘 근사할 수 있음을 보여주는 정리를 구성한다. 자세한 내용은 다음과 같다:
우리는 사전학습 데이터셋 가 특정 분포 에서 독립적이고 동일하게 분포된(i.i.d.) 방식으로 샘플링되었다고 가정한다. 또한, 사전학습 데이터 batch를 ground truth batch를 근사하는 데 사용하려면, 두 batch의 분포가 유사해야 한다는 필수 조건이 있다. 여기서는 단순화를 위해 이들 또한 i.i.d.라고 가정한다.
가정 A.1. 우리는 teacher model이 사용하는 ground-truth 데이터 batch 가 필터링이 필요한 사전학습 데이터셋 와 i.i.d. 관계에 있다고 가정한다.
단순화를 위해, batch 내의 cross-image-text 유사도를 , 로 표기한다. 그러면 정규화 항은 다음과 같이 쓸 수 있다:
여기서 이다. 우리는 가 충분히 클 때 모든 에 대해 임을 보일 것이다. 이는 랜덤 batch를 사용하여 ground-truth batch를 근사할 수 있음을 의미한다.
정리 A.1. 가정 A.1이 성립하고 batch size가 를 만족하면, 임의의 에 대해 이고 이다.
증명. 이므로, 임은 자명하다. 라고 두면, 는 평균이 0이다. 데이터가 i.i.d.이므로 도 i.i.d.이며, 로 표기한다. 임을 주목하면, Bernstein inequality에 의해 다음이 성립한다:
에 대해서도 유사한 결론이 성립한다. 이 결과들을 통해 적어도 의 확률로 다음을 얻는다:
따라서 우리는 를 얻는다. 더 나아가, 임의의 에 대해 임을 쉽게 증명할 수 있다. 그러므로 우리는 를 얻는다. 에 대해서도 유사한 주장이 성립한다.
A. 2 Optimality of NormSim Under Linear Assumption
이 섹션에서는 저품질 이미지와 불일치하는 텍스트가 이미 제거된 선형 모델 가정 하에서 일 때 NormSim metric에 대한 이론적 정당성을 제시한다. 즉, 우리는 주로 다음 전략에 초점을 맞춘다.
S=\arg \max _{|S|=N} \sum_{i \in S} \bar{f}_{v}\left(x_{i}^{v}\right)^{\top} \underbrace{\left(\frac{1}{\left|X_{\text {target }}\right|} \sum_{x_{t} \in X_{\text {target }}} \bar{f}_{v}\left(x_{t}^{v}\right) \bar{f}_{v}\left(x_{t}^{v}\right)^{\top}\right)}_{\bar{\Sigma}_{\text {target_proxy }}} \bar{f}_{v}\left(x_{i}^{v}\right)A.2.1 Theoretical Setup
학습 데이터 (Training data)
관측 가능한 이미지-텍스트 학습 쌍 에 대해, 우리는 관심 task에 대한 모든 의미론적으로 관련된 정보를 포함하는 해당 잠재 벡터(latent vector)를 로 정의한다. 이전 이론 연구 [46]와 유사하게, 우리는 각 i.i.d. 쌍 이 교차 공분산(cross-covariance)을 만족하는 zero-mean sub-gaussian 분포를 따른다고 가정한다:
그리고 각 은 선형 모델(linear model)에 기반하여 다음과 같이 생성된다:
여기서 는 잠재 벡터 공간에서 입력 공간으로의 orthonormal ground truth representation mapping이며, 는 i.i.d. 랜덤 노이즈이다. 또한, 우리는 임의의 유한 데이터셋 (예: 주어진 학습 세트 )의 교차 공분산을 로 표기한다.
테스트 데이터 (Test data)
임의의 zero-shot 다운스트림 task에 대해, 우리는 해당 task가 학습 세트와 거의 동일한 데이터 생성 프로세스를 공유한다고 가정한다. 단, 교차 공분산 은 반드시 과 같을 필요는 없으며, 이는 \bar{\Sigma}_{\text {target_proxy}}의 선택을 필요로 한다.
교사 모델로서의 CLIP embedding model (CLIP embedding model as teacher)
선형 모델 가정 하에, 우리는 교사 모델(teacher model) 을 가지며, 이 모델이 생성한 CLIP embedding은 ground truth hidden vector 을 오차를 포함하여 부분적으로 복구할 수 있다.
정식으로, 우리는 교사가 모든 가능한 개의 예산 부분집합 에 대해 오차를 가진다고 말한다:
여기서 동일한 표기법이 언어 모달리티에도 적용된다. ground truth 행렬 에 대한 orthonormal 가정에 따라, 는 매핑을 역전시키려는 목표를 가진다. 또한, 우리는 교사가 교차 모달 오차(cross modal error)를 가진다고 말한다:
모든 이 일 때 0으로 수렴하면, 우리는 교사가 두 모달리티 모두에 대해 강하다고 말한다. 그러나 시각 모달리티와 같이 하나의 모달리티만 강할 수도 있다. 즉, 이지만 일 수 있다.
모델 및 학습 (Model and training)
[46]의 Lemma 4.1에 따르면, CLIP loss를 사용하여 선형 모델을 최적화하는 것은 정규화된 선형 loss를 사용하는 것과 거의 동일한 학습 역학을 가진다. 따라서 여기서는 contrastive 쌍 간의 CLIP score 차이를 최대화하고 정규화 항을 추가하여 을 학습한다고 가정한다:
여기서 이고 는 정규화와 관련된 상수이다. 이 목적 함수는 자기 유사성(self-similarity)을 최대화하고 서로 다른 쌍 간의 유사성을 최소화한다. 이 "loss"는 음수일 수 있으며, 모든 값이 0인 자명한 해(trivial null solution)를 피한다. 우리는 주어진 로부터의 이 학습 과정을 로 표기한다.
목표 및 측정 지표 (Goal and metric)
학습 loss 함수와 동일한 원칙에 따라, 우리는 분포 을 가진 다운스트림 task에서 학습된 의 성능을 test loss 로 측정한다:
이는 다음 분류 정확도(classification accuracy)에서 영감을 받았다. 테스트 데이터가 개의 클래스를 포함하고 클래스 분포가 라고 가정한다. 모든 클래스 에 대해 학습 데이터 는 분포 를 만족한다. 우리는 또한 해당 분류 템플릿이 라고 가정한다. 따라서 분류 정확도를 다음과 같이 정의한다:
따라서 우리의 목표는 예산 제약 없이 임의의 에 대해 최적의 후방 부분집합(best hind-side subset)과의 차이를 최소화하는 것이다:
A.2.2 Generalization Guarantees
이제 이론적 보장을 제공하며, 증명은 Appendix A.2.3으로 미룬다. 먼저, NormSim 점수의 직관적 의미를 증명하고자 한다.
Lemma A.1 (NormSim의 직관적 의미). 높은 확률 로, 만약 후방 최적 부분집합(hind-side best subset)이 최소 개의 샘플을 가진다고 가정하면, 다음이 성립한다:
증명 스케치 (Proof sketch). (1) 이 모두 zero-mean이라는 가정 하에, clip score gap을 최대화하는 것은 동일한 샘플의 clip score를 최대화하는 것과 동등하다.
(2) Eckart-Young-Mirsky Theorem을 사용하여 정규화된 학습 손실 을 최소화함으로써, 의 닫힌 형식 해(closed form solution)를 얻는다.
(3) (2)와 (1)의 결과를 결합하면 다음을 얻는다.
동일한 분석이 에도 적용될 수 있다. 이 두 방정식을 재배열하면 최종 결과를 얻는다.
이 보조정리(lemma)는 가 NormSim 관련 항과 에서 비롯된 noise 항에 의존한다는 것을 보여준다. 과 가 충분히 크면, NormSim 관련 항이 지배적이 될 것이다. 이는 선택된 데이터의 수가 충분하다면 작은 변화에 최종 성능이 덜 민감하다는 우리의 실제 경험과 일치한다. 더욱이, 테스트 분포가 identity cross-variance를 가지는 일부 특수한 경우에는 CLIP score를 선택하는 것만으로도 충분할 수 있다.
이제 및 vision-only 정보의 선택에 대한 증명을 제시할 준비가 되었다. 구체적으로, 전략 오류(strategy error)는 주로 다음 두 가지에서 발생한다: (1) 학습과 테스트 간의 알 수 없는 테스트 분포 변화(unknown test distribution shift). (2) 관측 불가능한 ground truth . 오류 (1)을 해결하기 위해, 우리는 프록시 테스트 분산(proxy test variance) 을 사용하여 테스트에 대한 사전 지식을 가정한다. 오류 (2)를 해결하기 위한 두 가지 가능한 해결책은 다음과 같다. 이론적 해석에 기반하여, 우리는 teacher embedding model의 속성에 따라 다른 전략을 선택해야 한다.
Theorem A.2 (Main). Lemma A.1의 가정 하에,
첫째, 과 간의 차이가 클수록 기대할 수 있는 개선이 적다는 것은 명백하다. 둘째, 이 크고(언어 부분의 정확도가 낮음) 가 작은(비전 부분의 정확도가 높음) 시나리오에서는 vision-only embedding을 선택하는 것이 바람직할 수 있다. 그러나 학습자는 ground truth 시각 및 언어 잠재 벡터 간의 정렬(alignment)을 나타내는 항도 고려해야 한다. 이 항은 데이터의 본질적인 품질을 반영한다. 만약 이 항이 이미 상당하다면, 언어 정보의 프록시(proxy)로 시각 정보에만 의존하는 것은 최적 이하의 결과를 초래할 수 있다.
A.2.3 Detailed proofs
Lemma A.2. 다음을 가정하자.
그러면 다음이 성립한다.
여기서 noise term 는 (12), (13), (14), (15)에 정의되어 있다.
증명. 임을 주목하자. [46]의 Corollary B.1. 증명과 유사하게, 다음을 얻는다.
여기서 이다. Eckart-Young-Mirsky Theorem (예: Golub et al. [47]의 Theorem 2.4.8)에 의해 다음을 알 수 있다.
여기서 표기법은 행렬 의 첫 개 구성 요소를 선택하는 것을 의미한다. 또한 다음을 주목하자.
여기서 임을 주목하면, 는 다음과 같다.
행렬 의 랭크는 을 넘지 않으므로 이다. 그리고 에 대해, 는 인 noise term이다.
Lemma A.3. 임의의 고정된 에 대해, 높은 확률 로 noise term은 로 상한이 정해진다. 증명. P1과 P2의 상한을 정하기 위해 다음을 얻는다.
각 를 약하게 종속적인 변수로 간주하면, Bernstein 부등식을 사용하여 높은 확률 로 다음을 얻는다.
따라서 . Wainwright et al. [48]의 Proposition 2.5와 유사하게 임을 주목하면, 일 때 P3와 P4가 낮은 차수의 항임을 쉽게 알 수 있다.
Lemma A.4 (VAS의 직관). 높은 확률 로, 후방 최적 부분집합이 최소 개의 샘플을 가진다고 가정하면, 다음이 성립한다.
증명. 데이터셋 를 기반으로 학습된 임의의 에 대해 다음을 얻는다.
여기서 첫 번째 방정식은 Theorem A.4에서, 세 번째 방정식은 Lemma A.2에서 유래한다. 결과적으로 다음을 얻는다.
따라서 최종 결과는 다음과 같다.
\begin{aligned} \Delta(S) & =\mathcal{L}_{\text {test }}\left(\hat{G}_{v l}\right)-\min _{S^{\prime} \in D_{\text {train }}} \mathcal{L}_{\text {test }}\left(\mathcal{A}\left(S^{\prime}\right)\right) \\ & =\frac{1}{\rho} \max _{S^{\prime} \in D_{\text {train }}}\left(\operatorname{Tr}\left(\Sigma_{\text {target }}\left(\Sigma_{S^{\prime}}-\Sigma_{S}\right)\right)\right)+\mathcal{O}\left(\sqrt{\frac{d \log (1 / \delta)}{\underline{n}}}+\sqrt{\frac{d \log (1 / \delta)}{|S|}}\right) \end{aligned} $$ $\square$ Theorem A.3 (주요 정리). Lemma A.1의 가정 하에 다음이 성립한다.\begin{aligned} \Delta(S) & \leq \text { noise }+\left|\Sigma_{\text {target }}-\Sigma_{\text {target }}\right|\left|\Sigma_{S}-\Sigma_{\text {best }}\right|{*} \ & +\left{\begin{array}{l} \epsilon{v * l}^{S} \quad(\text { vision }+ \text { language }) \ \left(\epsilon_{v}^{S}+\sqrt{\left.1-\frac{1}{|S|} \sum_{i \in[S]}\left\langle\boldsymbol{z}^{v}, \boldsymbol{z}^{l}\right\rangle\right)}\right) \quad \text { (vision only) } \end{array}\right. \end{aligned}
**증명**. Lemma A.1을 기반으로, 부분집합 $S$를 선택함으로써 발생하는 오류, 즉 $\operatorname{Tr} \Sigma_{\text {target }} \Sigma_{S}$에 초점을 맞출 것이다. 정확한 $\Sigma_{\text {target }}$는 알 수 없으므로, 대신 일부 proxy $\Sigma_{\text{target}}$에 접근할 수 있다고 가정한다. 임의의 $S$에 대해 ground-truth $\Sigma_{S}=\mathbb{E}_{\boldsymbol{z}_{v l} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{l}\right)^{\top}$임을 상기하자. 불행히도, 이는 학습자가 직접 관찰할 수 없다. 대신 학습자는 teacher model $\bar{G}_{v l}$을 기반으로 일부 proxy $\bar{\Sigma}_{S}$를 관찰할 수 있으며, 따라서 다음을 해결한다.\underset{S}{\arg \max } \operatorname{Tr}\left(\bar{\Sigma}{\text {target }} \bar{\Sigma}{S}\right)
따라서 $\Sigma_{\text {best }}=\arg \max _{S^{\prime} \in D_{\text {train }}} \operatorname{Tr}\left(\Sigma_{\text {target }} \Sigma_{S^{\prime}}\right)$라고 하면\begin{aligned} \operatorname{Tr}\left(\Sigma_{\text {target }}\left(\Sigma_{\text {best }}-\Sigma_{S}\right)\right) & =\operatorname{Tr}\left(\bar{\Sigma}{\text {target }}\left(\Sigma{\text {best }}-\bar{\Sigma}{S}\right)\right)+\operatorname{Tr}\left(\bar{\Sigma}{\text {target }}\left(\bar{\Sigma}{S}-\Sigma{S}\right)\right)+\operatorname{Tr}\left(\left(\Sigma_{\text {target }}-\bar{\Sigma}{\text {target }}\right)\left(\Sigma{\text {best }}-\Sigma_{S}\right)\right) \ & \leq \operatorname{Tr}\left(\bar{\Sigma}{\text {target }}\left(\bar{\Sigma}{S}-\Sigma_{S}\right)\right)+\operatorname{Tr}\left(\left(\Sigma_{\text {target }}-\bar{\Sigma}{\text {target }}\right)\left(\Sigma{\text {best }}-\Sigma_{S}\right)\right) \ & \leq\left|\Sigma_{\text {target }}\right|\left|\bar{\Sigma}{S}-\Sigma{S}\right|{*}+\left|\bar{\Sigma}{\text {target }}-\Sigma_{\text {target }}\right|\left|\Sigma_{S}-\Sigma_{\text {best }}\right|_{*} \end{aligned}
여기서 첫 번째 부등식은 $\bar{\Sigma}_{S}$의 정의에 의한 것이고, 두 번째 부등식은 Holder 부등식에 의한 것이다. 이제 핵심은 우리가 선택한 전략을 기반으로 $\left\|\bar{\Sigma}_{S}-\Sigma_{S}\right\|_{*}$의 상한을 정하는 것이다. 옵션 1에서는 시각 및 언어 모달리티 모두에서 CLIP embedding을 사용한다. 즉, $\bar{\Sigma}_{S}=\sum_{\boldsymbol{x}_{v l} \in S}\left(\bar{G}_{v}\right)^{\top} \boldsymbol{x}^{v}\left(\boldsymbol{x}^{l}\right)^{\top} \bar{G}_{l}$를 선택한다. 그러면 다음을 얻는다.\left|\bar{\Sigma}{S}-\Sigma{S}\right|{*} \leq \frac{1}{|S|}\left|\sum{\boldsymbol{x}{v l} \in S}\left(\bar{G}{v}\right)^{\top} \boldsymbol{x}^{v}\left(\boldsymbol{x}^{l}\right)^{\top} \bar{G}{l}-\sum{\boldsymbol{x}{v l} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{l}\right)^{\top}\right|{*} \leq \epsilon_{v * l}^{S}
옵션 2에서는 언어 모델에서만 CLIP embedding을 사용한다. 즉, $\bar{\Sigma}_{S}= \sum_{\boldsymbol{x}_{v l} \in S} \bar{G}_{v}^{\top} \boldsymbol{x}^{v}\left(\boldsymbol{x}^{v}\right)^{\top} \bar{G}_{v}$를 선택한다. 그러면 $\epsilon_{S}$의 정의에 의해 다음을 얻는다.\begin{aligned} \left|\bar{\Sigma}{S}-\Sigma{S}\right|{*} & \leq \frac{1}{|S|}\left|\sum{\boldsymbol{x}{v l} \in S} \bar{G}{v}^{\top} \boldsymbol{x}^{v}\left(\boldsymbol{x}^{v}\right)^{\top} \bar{G}{v}-\sum{\boldsymbol{x}{v l} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{v}\right)^{\top}\right|{}+\frac{1}{|S|}\left|\sum_{\boldsymbol{x}{v l} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{v}\right)^{\top}-\Sigma{S}\right|_{} \ & \leq \epsilon_{v}^{S}+\frac{1}{|S|}\left|\sum_{\boldsymbol{x}{v l} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{v}\right)^{\top}-\Sigma{S}\right|_{*} \end{aligned}
\begin{aligned} \frac{1}{|S|}\left|\sum_{\boldsymbol{x}{v} \in S} \boldsymbol{z}^{v}\left(\boldsymbol{z}^{v}\right)^{\top}-\Sigma{S}\right|{*} & \leq \frac{1}{|S|}\left|Z{v}^{\top}\right|{*}\left|Z{v}-Z_{l}\right|{*} \ & =\frac{1}{|S|} \sqrt{\operatorname{Tr} Z{v} Z_{v}^{\top}} \sqrt{\operatorname{Tr}\left(Z_{v}-Z_{l}\right)^{\top}\left(Z_{v}-Z_{l}\right)} \ & =\frac{1}{|S|} \sqrt{\operatorname{Tr}\left(I_{n \times n}\right)} \sqrt{2 \operatorname{Tr}\left(I_{n \times n}-Z_{v} Z_{l}^{\top}\right)} \ & =\frac{1}{|S|} \sqrt{2|S|\left(|S|-\sum_{i \in[S]}\left\langle\boldsymbol{z}^{v}, \boldsymbol{z}^{l}\right\rangle\right)} \ & =\sqrt{\left.1-\frac{1}{|S|} \sum_{i \in[S]}\left\langle\boldsymbol{z}^{v}, \boldsymbol{z}^{l}\right\rangle\right)} \end{aligned}
따라서 증명을 마친다. Theorem A.4 (테스트 손실의 간략화된 버전). $\boldsymbol{z}_{v l}, \xi_{v l}$이 모두 zero-mean이라는 가정 하에, CLIP 점수 차이를 최대화하는 것은 동일한 샘플의 CLIP 점수를 최대화하는 것과 동일하다.\mathcal{L}{\text {target }}\left(G{v}, G_{l}\right):=-\mathbb{E}{\boldsymbol{x}{v l} \sim \mathcal{D}{\text {target }}}\left\langle G{v}^{\top} \boldsymbol{x}{v}, G{l}^{\top} \boldsymbol{x}_{l}\right\rangle
**증명**. 임의의 $\boldsymbol{x}_{v l}$에 대해 다음을 얻는다.\begin{aligned} & \mathbb{E}{\boldsymbol{x}{v l}^{\prime} \sim \mathcal{D}{\text {target }}}\left(\left\langle G{v}^{\top} \boldsymbol{x}{v}, G{l}^{\top} \boldsymbol{x}{l}^{\prime}\right\rangle-\left\langle G{v}^{\top} \boldsymbol{x}{v}, G{l}^{\top} \boldsymbol{x}{l}\right\rangle\right) \ & =\left\langle G{v}^{\top} \boldsymbol{x}{v}, G{l}^{\top} \mathbb{E}{\boldsymbol{x}{v l}^{\prime} \sim \mathcal{D}{\text {target }}}\left(\boldsymbol{x}{l}^{\prime}-\boldsymbol{x}{l}\right)\right\rangle \ & =-\left\langle G{v}^{\top} \boldsymbol{x}{v}, G{l}^{\top} \boldsymbol{x}_{l}\right\rangle \end{aligned}
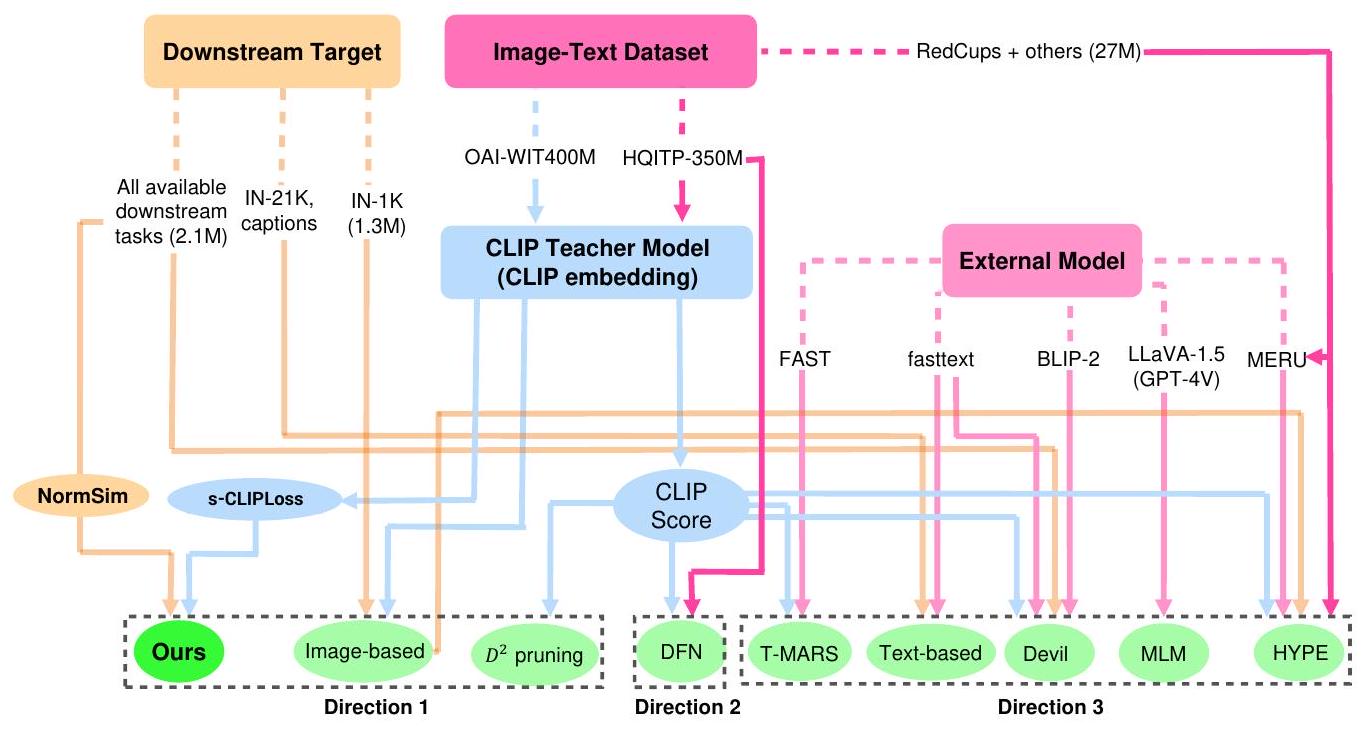 Figure 4: 멀티모달 contrastive learning을 위한 **데이터 선택 방법의 다양한 방향**을 보여주는 그림. 여기서는 우리가 얻을 수 있는 네 가지 주요 자원을 네 가지 색상으로 나타낸다: **CLIP teacher model, 다운스트림 target 데이터(외부 멀티모달 데이터셋 또는 사전학습 데이터셋보다 훨씬 작음), 외부 이미지-텍스트 데이터셋, 외부 non-CLIP 모델**. **Direction 1**은 **원래 OAI CLIP teacher model과 다운스트림 target 데이터만 사용하는 방법**을 나타낸다. **Direction 2**는 **외부 데이터셋을 사용하여 새로운 CLIP teacher model을 학습시켜 필터링을 개선하는 방법**을 나타내며, DFN \[2]과 같은 방식이다. **Direction 3**은 **외부 non-CLIP 모델을 사용하여 다운스트림 task에 휴리스틱하게 도움이 될 수 있는 데이터(예: 텍스트가 너무 많지 않거나 더 특별한 이미지)를 선택하는 방법**을 나타낸다. 일반적으로 **CLIP embedding만 사용하는 D1 방법(예: s-CLIPLoss)은 D2와 직교**한다. 그리고 **D1과 D2 모두 D3와 결합하여 더 나은 필터링 결과**를 탐색할 수 있다. 본 논문의 실험 부분(Sec.4)에서는 우리가 제안한 **D1 방법인 NormSim과 s-CLIPLoss가 최고의 방법인 "HYPE $\cup$ DFN"을 제외한 모든 D3 baseline보다 우수한 성능**을 보임을 추가로 보여준다. 그리고 **우리의 방법을 해당 방법과 결합하여 새로운 state-of-the-art를 달성**할 수 있다. ## B Illstration of Different Directions for Data Selection in Multimodal Contrastive Learning 우리는 현재 최고의 데이터 선택 방법들을 분류하는 우리의 주요 아이디어를 Figure 4에 요약하였다. ## C Details of Experiments ## C. 1 Computation Cost 우리 알고리즘은 **Table 5**에서 보여주듯이 **기존의 많은 연구들에 비해 계산 비용을 크게 줄일 수 있다.** 예를 들어, **CLIP embedding을 얻는 데 약 50시간(CLIP-B/32 기준)이 소요**된 후에도, **T-MARS \[12]와 MLM \[42]은 DataComp-medium의 110M 크기 데이터셋에서 필요한 정보를 추출하는 데 여전히 900시간 이상의 데이터 전처리 시간이 필요**하다. 반면, **우리는 약 5시간만 필요**하다. 한편, DFN은 유사한 forward 속도(즉, 전처리 시간)를 가지지만, DataComp-medium보다 큰 HQITP-350M에서 새로운 CLIP teacher 모델을 재학습해야 한다. 다른 방법들의 전처리 시간 추정에 대한 세부 정보는 다음과 같다: * **T-MARS**와 $\mathbb{D}^{2}$ pruning의 경우, 우리는 **DataComp-small (11M) 데이터에 대해 공식 코드를 실행**했으며, **T-MARS의 전처리 시간이 사전학습 데이터셋 크기에 비례**하고 $\mathbb{D}^{2}$ pruning이 선형보다 빠르지 않다는 점을 고려하여, **DataComp-medium에 대해서는 전처리 시간을 단순히 10배로 스케일링**했다. Table 5: 우리 방법과 다른 D3 카테고리 방법들 간의 전처리 시간 및 필요한 외부 리소스 비교. DFN은 우리 s-CLIPLoss 방법과 직교하며 Table 2에서 언급했듯이 직접 개선할 수 있으므로 생략한다. 여기서는 MLM을 제외한 모든 baseline이 사전학습된 CLIP 모델을 사용하므로, CLIP 이미지/텍스트 embedding 추론 시간(OAI CLIP-B/32의 경우 약 50 L40 시간)은 계산에 포함하지 않는다. 이는 DataComp 벤치마크 \[1]에서도 채택된 방식이다. 외부 데이터셋은 외부 모델을 학습하거나 fine-tuning하는 데 사용된 외부 멀티모달 데이터셋을 의미한다. 특히, 다음 방법들의 전처리 시간은 모두 필터링되지 않은 사전학습 데이터셋의 양에 거의 선형적으로 비례한다. | Type | Filtering Strategy | Ext. Model Used | Size of Ext. Dataset | Preprocess Time | Training Time | Avg. | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | D1 | $\mathbb{D}^{2}$ Pruning [18] | NA | NA | $>70 \mathrm{~L} 40 \mathrm{~h}$ | 65 L 40 h | 29.5 | | D3 | T-MARS [12] | FAST [13] | NA | 950 L 40 h | 65 L 40 h | 34.1 | | D3 | MLM [42] | LLaVA-1.5 [43, 44] | 50k | 1120 A100 h | 65 L 40 h | 34.5 | | D3 | Devil [14] | fasttext [15], BLIP-2 [16] | NA | 510 A 100 h | 65 L 40 h | 34.5 | | D3 | HYPE [3] | MERU [45] | 27M | $>120 \mathrm{~L} 40 \mathrm{~h}$ | 65 L 40 h | 31.9 | | D1 | Ours (20%) | NA | NA | 5 L 40 h | 65 L 40 h | 35.2 | * **MLM**의 경우, 우리는 **논문에서 제시된 추정 시간**을 사용했다. 그들은 A100에서 10k 샘플을 처리하는 데 6.1분이 필요하다고 언급했으며, 이는 우리 데이터셋(110M)에 대해 **1120 A100 시간**에 해당한다. 그들의 CLIP embedding 계산 시간 추정치는 부정확하며, 우리는 DataComp 파이프라인을 사용하여 그들의 주장보다 훨씬 빠르게 처리할 수 있다는 점을 언급해야 한다. * **Devil**의 경우, embedding 공간에서 **faiss 라이브러리의 k-means clustering 알고리즘을 실행**해야 하며, 이는 DataComp-medium에서 **120 L40 시간**이 소요될 것으로 추정된다. BLIP-2 \[16]를 사용하여 전체 데이터셋을 스캔하는 데는 \[17]의 실험 세부 정보에 따르면 약 **470 A100 시간**이 필요하다. https://lambdalabs.com/gpu-benchmarks를 참조하여, k-means clustering의 경우 120 L40 시간이 최소한 40 A100 시간과 비슷하다고 대략적으로 가정한다. * **HYPE**의 경우, MERU가 CLIP만큼 효율적이라고 주장하지만, 최종 점수를 위해 110M 데이터를 처리하는 데 **최소 120 L40 시간**이 여전히 필요하다. 이는 k-means clustering 알고리즘을 실행하여 얻은 DataComp-medium의 이미지 embedding 클러스터를 사용하기 때문이다. ## C. 2 Details of s-CLIPLoss 우리는 Algorithm 1에서 **s-CLIPLoss** 계산을 위한 **pseudocode**를 제공한다. 이 pseudocode는 **PyTorch 스타일의 병렬 행렬 계산에 특화**되어 있다. **완전히 가속화**될 수 있으며, **정규화 항(normalization term)으로 인해 발생하는 계산 비용은 Table C.1에 상세히 설명된 다른 최고 성능 baseline 모델들의 학습 시간이나 전처리 시간에 비해 무시할 수 있는 수준**이다. **s-CLIPLoss**에서는 **teacher model 사전학습 단계의 마지막 스텝에서 batch size $|B|$와 학습 가능한 온도 파라미터 $\tau$의 값**을 알아야 한다. **OAI CLIP-L/14**와 **OAI CLIP-B/32**의 경우, 이 값들은 각각 **$\tau=0.01$ 및 $|B|=32768$**이다. 우리는 또한 **Table 6**에서 볼 수 있듯이, **CLIP teacher model에 선택된 온도 파라미터와 batch size에 대한 ablation study**를 수행했다. 일반적으로 **더 큰 batch size가 더 나은 성능을 가져오며**, **$\tau=0.01, b=32768$이 OAI CLIP-B/32와 DFN-P 모두에게 최적의 선택**임을 확인할 수 있다. 이러한 batch size를 사용하는 이유는 **더 큰 batch가 더 많은 contrastive 데이터 쌍을 포함할 수 있기 때문**이며, 이는 **Appendix A.1에서 증명된 정규화 항의 집중 결과(concentration result)에 의해서도 뒷받침**된다. 따라서 **더 많은 다양한 데이터 간의 이미지-텍스트 매칭을 확인할 수 있다.** 그러므로 우리는 **CLIP forward pass에서 단일 24G GPU에 들어갈 수 있는 가장 큰 batch size인 32768**을 항상 고려하며, 이는 **OAI CLIP 학습 batch size와도 동일**하다. ## C. 3 Details of NormSim ${ }_{2}$-D 이 섹션에서는 **$\mathrm{NormSim}_{2}-\mathrm{D}$ 알고리즘의 세부 사항**을 설명한다. **Top-$N$ 선택 방법**은 다음 목표를 달성하는 것을 목표로 한다:S=\arg \max {|S|=N} \sum{i \in S} \bar{f}{v}\left(x{i}^{v}\right)^{\top}\left(\frac{1}{\left|X_{\text {target }}\right|} \sum_{x_{t} \in X_{\text {target }}} \bar{f}{v}\left(x{t}^{v}\right) \bar{f}{v}\left(x{t}^{v}\right)^{\top}\right) \bar{f}{v}\left(x{i}^{v}\right)
Table 6: **CLIP teacher model의 temperature 파라미터 $\tau$와 batch size $b$에 대한 ablation study.** teacher model의 마지막 학습 단계에서 얻은 값은 OAI CLIP-B/32, OAI CLIP-L/14의 경우 $\tau=0.01, b=32768$이며, DFN-P의 경우 $b=16384, \tau=0.07$이다. 본 논문에서는 세 가지 teacher model 모두에 대해 $b=32768, \tau=0.01$을 사용한다. | OAI CLIP-B/32 | Size | IN-1k | IN Dist. Shift | VTAB | Retr. | Avg. | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | CLIPScore (30%) [38] | 33 M | 27.6 | 24.2 | 33.6 | 25.1 | 33.2 | | s-CLIPLoss (30%) | | | | | | | | $b=16384, \tau=0.01$ | 33M | 28.8 | 25.0 | 32.5 | 26.2 | 33.0 | | $b=16384, \tau=0.02$ | 33M | 28.6 | 24.8 | 33.3 | 25.3 | 33.1 | | $b=16384, \tau=0.07$ | 33 M | 28.0 | 24.2 | 33.5 | 25.1 | 32.6 | | $b=32768, \tau=0.001$ | 33 M | 16.0 | 13.9 | 25.1 | 19.4 | 24.4 | | $b=32768, \tau=0.005$ | 33 M | $\underline{28.5}$ | $\underline{25.0}$ | $\underline{33.6}$ | 27.0 | $\underline{33.0}$ | | $b=32768, \tau=0.01$ | 33 M | 28.8 | 25.1 | 33.7 | $\underline{26.6}$ | 33.6 | | $b=32768, \tau=0.02$ | 33 M | $\underline{28.5}$ | 24.8 | 33.6 | 26.2 | 32.9 | | $b=32768, \tau=0.07$ | 33 M | 28.2 | 24.5 | 32.8 | 25.2 | 32.7 | | s-CLIPLoss (30%) $\cap$ NormSim ${ }_{\infty}$ (Target) | | | | | | | | $b=16384, \tau=0.01$ | 22 M | 32.4 | 27.4 | 34.5 | 26.1 | 34.7 | | $b=16384, \tau=0.02$ | 22 M | 31.8 | 26.7 | 35.0 | 24.9 | 34.2 | | $b=16384, \tau=0.07$ | 22 M | 31.0 | 26.3 | 35.0 | 25.5 | 33.9 | | $b=32768, \tau=0.005$ | 22 M | 32.2 | 27.2 | 35.3 | 26.5 | 34.8 | | $b=32768, \tau=0.01$ | 22 M | 32.4 | 27.4 | 35.9 | 26.3 | 35.2 | | DFN-P | Size | IN-1k | IN Dist. Shift | VTAB | Retr. | Avg. | | s-CLIPLoss | | | | | | | | $15 \%, b=16384, \tau=0.07$ | 16M | 31.0 | 27.0 | 35.2 | 26.8 | 34.2 | | $15 \%, b=32768, \tau=0.01$ | 16M | 31.3 | $\underline{27.3}$ | 35.8 | 26.4 | $\underline{34.6}$ | | $17.5 \%, b=16384, \tau=0.07$ | 19M | 31.3 | 27.2 | 33.5 | 27.6 | 33.5 | | $17.5 \%, b=32768, \tau=0.01$ | 19M | 31.2 | 27.5 | 35.7 | $\underline{27.0}$ | 34.7 | | s-CLIPLoss $(17.5 \%) \cap$ NormSim ${ }_{\infty}^{\mathbf{B} / \mathbf{3 2}}$ (Target) | | | | | | | | $b=16384, \tau=0.07$ | 16M | 31.1 | 27.4 | 34.8 | 26.1 | 34.2 | | $b=32768, \tau=0.01$ | 16M | 31.6 | 27.3 | 37.2 | 25.5 | 35.7 | 실제 $X_{\text {target }}$이 알려지지 않은 경우이다. 실제로는 한 번에 하나의 데이터를 제거하는 것은 너무 느리다. 따라서, 우리는 **매 단계마다 데이터 배치를 제거**한다. 구체적으로, 단계의 수가 $\tau$이고, $\bar{\Sigma}_{\text {test }, i}= \frac{1}{\left|S_{i}\right|} \sum_{j \in S_{i}} \bar{f}_{v}\left(\boldsymbol{x}_{j}^{v}\right) \bar{f}_{v}\left(\boldsymbol{x}_{j}^{v}\right)^{\top}$라고 할 때, 여기서 $S_{i}$는 $i$단계에서 선택된 부분집합이다. 우리는 **최종 부분집합 크기에 도달할 때까지 다음 방정식을 만족하는 데이터를 단계별로 제거**한다:S_{i} \backslash S_{i+1}=\arg \min {x{l} \in S_{i}}\left[\bar{f}{v}\left(x{l}^{v}\right)^{T} \cdot\left(\frac{1}{\left|S_{i}\right|} \sum_{x_{t} \in S_{i}} \bar{f}{v}\left(x{t}^{v}\right) \bar{f}{v}\left(x{t}^{v}\right)^{\top}\right) \cdot \bar{f}{v}\left(x{l}^{v}\right)\right], \quad i \in{0, \ldots, \tau-1}
그러면 Algorithm 2에서 **$\mathrm{NormSim}_{2}$-D의 알고리즘 프로세스**를 자세히 설명할 수 있다. 일반적으로 **단계 크기가 작을수록 결과가 더 좋다.** 하지만 실험에서는 **$\tau=500$일 때도 좋은 결과를 얻기에 충분**하다는 것을 발견했다. ## C. 4 Details of Related Works 우리는 본 논문에서 사용된 baseline에 대한 몇 가지 세부 정보를 다음과 같이 추가한다. * **Text-based filtering.** \[1]은 **ImageNet-21K 또는 ImageNet-1K의 클래스 이름과 겹치는 캡션을 포함하는 데이터**를 선택하려는 **텍스트 기반 필터링**을 제안한다. * **Image-based filtering.** \[1]은 또한 **ImageNet-1K 클래스와 시각적 콘텐츠가 겹치는 데이터를 샘플링하는 휴리스틱 방식**을 제안한다. 이들은 먼저 **언어(fasttext \[15]를 사용하여 영어 캡션만 선택) 및 캡션 길이(두 단어 이상, 5자 이상)로 필터링**을 적용한다. 그런 다음 **학습 데이터의 이미지 임베딩을 Faiss \[49]를 사용하여 100K 그룹으로 클러스터링**하고, **클러스터 중심이 ImageNet-1K 이미지의 최소 하나 이상의 이미지 임베딩에 가장 가까운 그룹**을 유지한다. ``` Algorithm 1 s-CLIPLoss Inputs: pretraining 데이터의 이미지/텍스트 임베딩 \(F^{v l}=\left[\left\{\bar{f}_{v l}\left(x_{1}^{v l}\right)\right\}, \ldots,\left\{\bar{f}_{v l}\left(x_{N}^{v l}\right)\right\}\right]^{\top} \in\) \(\mathbb{R}^{N \times d}\), 배치 크기 \(b\), 온도 파라미터 \(\tau\), s-CLIPLoss가 무작위로 계산되는 횟수 \(K(=10)\). s-CLIPLoss 배열 \(\boldsymbol{r}=[0, \ldots, 0] \in \mathbb{R}^{N}\) 초기화 for \(k=1\) to \(K\) do 무작위 배치 분할 \(S_{k}=\left\{B_{1}, \ldots, B_{s}\right\}\)을 얻는다. 여기서 \(s=\lceil N / b\rceil\). 모든 \(B_{i} \in S_{k}\)는 데이터 배치의 인덱스이다. for \(j=1\) to \(s\) do 배치 \(j\)의 임베딩 배치 얻기: \(F_{j}^{v l}=F^{v l}\left[B_{j}\right] \in \mathbb{R}^{b \times d}\) 유사도 행렬 얻기: \(E_{j}=F_{j}^{v}\left(F_{j}^{l}\right)^{\top} \in \mathbb{R}^{b \times b}\) CLIPScores 얻기: \(\boldsymbol{c}_{j}=\operatorname{diag}\left(E_{j}\right) \in \mathbb{R}^{b}\) \(G_{j}=\exp \left(E_{j} / \tau\right)\) 정의 \(\boldsymbol{g}_{j}^{v} \in \mathbb{R}^{b}\)를 \(G_{j}\)의 각 행 벡터의 합(즉, 이미지에 대한 합)을 포함하는 벡터로 정의한다. \(\boldsymbol{g}_{j}^{l} \in \mathbb{R}^{b}\)를 \(G_{j}\)의 각 열 벡터의 합(즉, 텍스트에 대한 합)을 포함하는 벡터로 정의한다. s-CLIPLoss 얻기: \(\boldsymbol{r}\left[B_{j}\right]=\boldsymbol{c}_{j}-0.5 \tau \cdot\left(\log \left(\boldsymbol{g}_{j}^{v}\right)+\log \left(\boldsymbol{g}_{j}^{v}\right)\right)\), 여기서 요소별(element-wise) 연산을 사용한다. end for end for 각 무작위 분할의 평균을 출력으로 취한다: s-CLIPLoss \(=\boldsymbol{r} / K\) ``` ``` Algorithm 2 NormSim-D strategy Inputs: CLIP score 필터링 후 데이터의 이미지 임베딩 \(\left\{\bar{f}_{v}\left(x_{i}^{v}\right)\right\}_{i \in S}\), 목표 크기 \(N\), 단계 수 \(\tau\) \(S_{0}=S, N_{0}=|S|\) 초기화 for \(t=1\) to \(\tau\) do 단계 \(t\)에서의 크기: \(N_{t}=N_{0}-\frac{t}{\tau}\left(N_{0}-N\right)\). 사전 행렬: \(\bar{\Sigma}_{\text {test }, t-1}=\sum_{j \in S_{t-1}} \bar{f}_{v}\left(x_{j}^{v}\right) \bar{f}_{v}\left(x_{j}^{v}\right)^{\top}\) \(S_{t-1}\)의 각 샘플 \(i\)에 대해 업데이트된 NormSim \({ }_{2}\)-D: \(\operatorname{NormSim}_{2}-\mathrm{D}\left(x_{i}\right)=\bar{f}_{v}\left(x_{i}^{v}\right)^{\top} \cdot \bar{\Sigma}_{\text {test }, t-1} \cdot \bar{f}_{v}\left(x_{i}^{v}\right)\) \(S_{t-1}\)에서 가장 높은 NormSim \({ }_{2}\)-D를 가진 데이터를 포함하고 \(\left|S_{t}\right|=N_{t}\)를 만족하는 \(S_{t}\)를 구성한다. end for ``` * **$\mathbb{D}^{2}$ Pruning.** \[18]은 **코어셋 선택을 위해 데이터셋을 무방향 그래프로 표현**하려고 시도한다. 이들은 각 예시에 대한 **난이도(difficulty)를 할당**하고, **메시지 전달(message passing)을 사용하여 이웃 예시의 난이도를 통합하여 난이도 점수를 업데이트**하며, 최종적으로 **다양하고 어려운 부분집합을 모두 유지**하려고 한다. 우리의 실험에서는 DataComp에 대한 $\mathbb{D}^{2}$의 기본 하이퍼파라미터를 공식 코드베이스에 명시된 대로 따른다. * **T-MARS** \[12]는 **FAST \[13]와 같은 텍스트 감지 모델을 사용하여 이미지 내 캡션 텍스트만 포함하고 다른 유용한 이미지 feature가 없는 데이터를 필터링**한다. * **Devils** \[14]는 **데이터 필터링을 위한 여러 방법들을 결합**한다. 처음에는 **텍스트 길이, 텍스트 빈도, 이미지 크기**와 같은 **휴리스틱 규칙**을 기반으로 데이터를 필터링하고, **CLIPScore를 사용하여 cross-modality 매칭**을 수행한다. 그런 다음 **이미지 기반 필터링과 유사한 대상 분포 정렬 방법**을 채택하지만, **ImageNet-1k만 사용하는 대신 22개의 다운스트림 task를 대상 세트로 사용**한다. 또한, **외부 모델 fasttext \[15]를 사용하여 비영어 캡션을 제거**하고, **이미지 캡셔닝 모델 BLIP-2 \[50]를 사용하여 MNIST 스타일 숫자가 있는 이미지를 선택**한다. * **MLM** \[42]은 **GPT-4V에 prompt를 주어 이미지-텍스트 데이터를 포함하는 instruction 데이터를 구성**하고, 이를 사용하여 **LLaVA-1.5 \[43, 44]와 같은 더 작은 vision-language model을 필터링 네트워크로 fine-tuning**한다. 그럼에도 불구하고, LLaVA-1.5의 파라미터 수는 여전히 CLIP보다 훨씬 많으며, 따라서 Table C.1에 언급된 바와 같이 LLaVA-1.5는 **훨씬 더 긴 전처리 시간**을 필요로 한다. ## C. 5 How to Choose Hyperparameters 우리의 **s-CLIPLoss**와 **NormSim**의 주요 하이퍼파라미터는 **필터링을 위한 목표 개수**이다 (온도 및 배치 크기 설정은 Appendix C.2 참조). 이는 DFN, MLM, T-MARS와 같은 모든 상위 baseline에서도 주요 관심사이다. **DataComp 설정**의 경우, DataComp-medium 벤치마크의 모든 상위 baseline이 **최고의 결과를 얻기 위해 15%에서 30% 범위의 downsampling 비율을 유지**한다는 점을 고려하여, 우리는 **샘플링 비율을 이전 baseline들과 유사하게 설정**할 수 있다. 우리의 방법은 OAI CLIP teacher model을 사용하여 먼저 **상위 30%의 s-CLIPLoss를 가진 데이터를 선택**하고, 그 다음 **상위 66.7%의 NormSim 점수를 가진 데이터를 선택**하여 **원래 풀의 20%를 유지**한다. 우리는 공정한 비교를 위해 여기서 목표 크기를 신중하게 튜닝하지 않았다. 더 일반적인 경우, **NormSim**은 점수가 풀 내의 다른 데이터가 아닌 **norm $p$와 목표 데이터에만 의존**하므로, **학습 데이터셋에 독립적인 임계값**을 권장할 수 있다. 일반적으로 **$\mathrm{NormSim}_{\infty}$ (Target)의 경우 0.7**, **$\mathrm{NormSim}_{2}$ (IN1k)의 경우 0.15**를 임계값으로 설정하는 것을 권장한다. 반면 **s-CLIPLoss**의 경우, NormSim과 마찬가지로 **CLIPScore도 학습 데이터셋에 독립적**이므로, 먼저 **CLIPScore가 0.21인 데이터의 백분위수를 찾은 다음**, 해당 백분위수에 도달할 때까지 **s-CLIPLoss를 사용하여 데이터셋을 downsample**하는 것을 권장한다. 전반적으로, **데이터 선택 알고리즘에 대한 최적의 필터링 비율을 찾는 것은 항상 어렵고 본 논문의 범위를 벗어난다.** 데이터 필터링을 위한 스케일링 법칙에 대한 논문 \[51]에 따르면, **downsampling 크기는 계산 예산에도 의존**한다. 예산이 많을수록 학습을 위해 더 많은 데이터를 샘플링해야 한다. 따라서 또 다른 가능한 해결책은 **그들의 fitting formula를 사용하여 권장 downsampling 비율을 얻는 것**이다. 마지막으로, 데이터 선택 문제에서 **시각화는 파라미터를 튜닝하거나 downsampling 비율을 찾는 간단하지만 효과적인 방법**이라는 점도 언급한다. 사람들은 먼저 일부 사전학습 데이터셋에서 **작은 부분집합(예: 1000개 데이터)을 무작위로 선택**한 다음, 그 데이터에 대해 **목표 점수(CLIPScore, s-CLIPLoss, NormSim 또는 기타 모든 지표)를 계산**하고, 마지막으로 **s-CLIPLoss의 하위 10%, 30%, 50%, 70%와 같이 다른 백분위수에서의 점수에 해당하는 데이터를 시각화**할 수 있다. 이러한 방식으로 **데이터를 관찰하여 필터링 임계값을 직접 결정**할 수 있다. 우리는 또한 Appendix E에 우리 방법의 시각화 예시를 제공한다. 우리는 이것이 **초기 downsampling 비율을 대략적으로 선택하는 방법에 대한 지침을 제공하는 효과적인 방법**이라고 믿는다. ## C. 6 Discussion of NormSim ## C.6.1 How NormSim ${ }_{2}$ Connects to Selecting the Data in Principal Components. 편의를 위해, 우리는 **타겟 데이터 $x_t \in X_T$의 이미지 임베딩을 $f(x_t)$로, 학습 데이터 $x_s \in X_S$의 이미지 임베딩을 $f(x_s)$로 표기**한다. 이때, **데이터 $x_s$에 대한 NormSim의 정의**는 다음과 같다:\operatorname{NormSim}{p}\left(X{T}, x_{s}\right)=\left(\sum_{x_{t} \in X_{T}}\left[f\left(x_{t}\right)^{\top} f\left(x_{s}\right)\right]^{p}\right)^{1 / p}
$p=2$일 때, 우리는 다음을 얻는다:\begin{aligned} \operatorname{NormSim}{2}\left(X{T}, x_{s}\right) & =\quad\left(\sum_{x_{t} \in X_{T}}\left[f\left(x_{s}\right)^{\top} f\left(x_{t}\right)\right] \cdot\left[f\left(x_{t}\right)^{\top} f\left(x_{s}\right)\right]\right)^{1 / 2} \ & =\quad\left(f\left(x_{s}\right)^{\top} \cdot \sum_{x_{t} \in X_{T}}\left[f\left(x_{t}\right) f\left(x_{t}\right)^{\top}\right] \cdot f\left(x_{s}\right)\right)^{1 / 2} \ & \propto \quad\left[f\left(x_{s}\right)^{\top}\left(\frac{1}{\left|X_{T}\right|} \sum_{x_{t} \in X_{T}} f\left(x_{t}\right) f\left(x_{t}\right)^{\top}\right) f\left(x_{s}\right)\right]^{1 / 2} \end{aligned}
여기서 $\Lambda=\frac{1}{\left|X_{T}\right|} \sum_{x_{t} \in X_{T}} f\left(x_{t}\right) f\left(x_{t}\right)^{\top}$는 **타겟 이미지 임베딩의 분산 행렬(variance matrix)**이다. NormSim$_2$를 필터링에 사용하면 다음과 같다:\begin{aligned} S & =\arg \max {|S|=N} \sum{x_{s} \in X_{S}} \operatorname{NormSim}{2}\left(X{T}, x_{s}\right) \ \operatorname{NormSim}{2}\left(X{T}, x_{s}\right) & =f\left(x_{s}\right)^{\top} \cdot \Lambda \cdot f\left(x_{s}\right) \ & =f\left(x_{s}\right)^{\top} U \cdot S \cdot U^{\top} f\left(x_{s}\right) \ & =\sum_{j=1}^{r} s_{j} \cdot\left[f\left(x_{s}\right)^{\top} u_{j}\right]^{2} \end{aligned}
여기서 $\Lambda=U S U^{\top}$는 $\Lambda$의 **고유값 분해(eigen decomposition)**이며, $S=\operatorname{diag}\left(s_{1}, \ldots, s_{r}\right)$는 $s_{1}>\ldots>s_{r}$을 만족하는 **고유값(eigenvalues) 행렬**이고, $U=\left[u_{1}, \ldots, u_{r}\right] \in \mathbb{R}^{d \times r}$는 **해당 고유벡터(eigenvectors), 즉 주성분 방향(principal component directions)**이다. $U$의 열 벡터와 $f(x_s)$는 모두 **단위 벡터(unit vectors)**이며, (24)식은 **NormSim$_2$가 주성분, 즉 큰 고유값 $s_j$를 가진 고유 방향 $u_j$와 일치하는 데이터를 선택**함을 보여준다. ## C.6.2 Why NormSim works well without explictly considering data diversity. 우리는 이 질문에 대해 다음과 같은 이유로 답변한다: * DFN 및 T-MARS와 같은 많은 **최고 수준의 baseline 모델**들도 **다양성(diversity)을 명시적으로 고려하지 않음에도 불구하고 여전히 좋은 성능**을 제공한다. Devil 연구에서는 **가치 있는 데이터는 여러 번 샘플링할 가치가 있다**고 주장하며 이를 "**quality duplication**"이라고 부른다. 따라서 NormSim이 다양성을 명시적으로 고려하지 않고도 잘 작동하는 중요한 이유 중 하나는, **DataComp 벤치마크와 같이 연산 예산이 제한된 상황에서 모델이 가장 유용하고 대표적인 데이터를 먼저 학습해야 하며, 이러한 데이터는 특정 target 데이터와 유사해야 하기 때문**일 수 있다. * 또한, 우리는 **ImageNet부터 EuroSet에 이르는 24개 downstream task에서 validation 데이터를 선택**했는데, 이는 NormSim이 유사도를 계산하기에 **충분히 다양한 범위의 target example을 포함**했을 수 있다. **target 데이터의 다양성은 결과적으로 선택된 subset의 다양성으로 이어질 것**이다. 이는 또한 **좋은 target 데이터셋을 선택하는 것의 중요성**을 시사한다. * 추가적인 이유는 **우리가 제안한 s-CLIPLoss가 이미 암묵적으로 더 다양한 데이터를 선택**한다는 점일 수 있다. 이는 본 논문의 Figure 1에 나타나 있다. **일부 학습 데이터가 다양하다면, 다른 데이터와의 매칭 정도가 낮아져 normalization term이 더 작아질 것**이다. 이는 **더 큰 s-CLIPLoss로 이어지고, 결과적으로 샘플링될 확률이 높아진다.** ## D Additional Results ## D. 1 Stability Analysis of Batch Sampling Numbers in s-CLIPLoss 우리는 **s-CLIPLoss**가 Figure 5에서 보여주듯이 **무작위로 선택된 배치(random select batches)의 수 $K$에 민감하지 않음**을 보인다. ## D. 2 Universality of s-CLIPLoss over Different Teacher Models 우리는 **OAI CLIP-B/32** 및 **DFN-P**와 같은 다양한 teacher model에 우리의 방법을 적용한 **완전한 결과**를 **Table 7**에 제시한다. 자세한 설명은 **Sec. 4**에 있다. ## D. 3 NormSim $_{\infty}$ is Better than Nearest Neighbor Selection 우리는 또한 **다운스트림 분포를 정렬하기 위해 near-neighbor selection**을 시도한다. 여기서 우리는 **각 target에 대한 사전학습 데이터의 순위(rank)를 계산**하고(순위가 높을수록 유사도가 높음), **각 사전학습 데이터에 대해 가장 높은 순위를 유지**한다. 마지막으로, **가장 높은 순위를 가진 데이터를 nearest neighbor selected subset으로 선택**한다. **Table 8**에서 우리는 **22개 다운스트림 task의 학습 데이터가 주어졌을 때**, **동일한 downsampling ratio 하에서 우리의 NormSim$_{\infty}$가 near-neighbor selection보다 우수한 성능**을 보인다는 것을 보여준다. 그 이유는 **target과 사전학습 세트 간의 분포가 잘 정렬되지 않았기 때문**일 수 있다. 만약 알고리즘이 **각 target에 대해 가장 가까운 학습 데이터를 찾도록 강제**한다면, 그 학습 데이터는 때때로 **무작위적이고 도움이 되지 않을 수 있다.** 반면에 **NormSim$_{\infty}$는 이러한 종류의 데이터를 선택하지 않는다.** 이는 단순히 순위만을 고려하는 대신, **최고 유사도 점수가 특정 일반 임계값을 초과하는 데이터를 선택**한다. 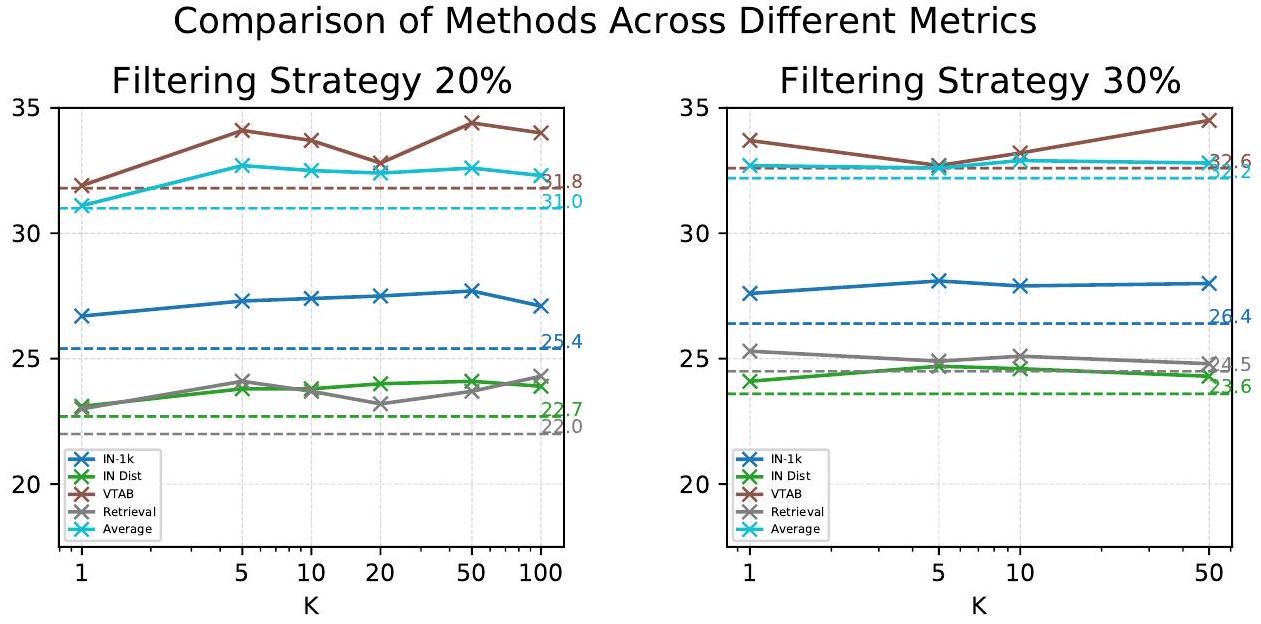 Figure 5: **DataComp-medium**에서 **다양한 batch sample 수($K$로 표시)에 따른 s-CLIPLoss 결과**. 실선은 **s-CLIPLoss**를, 점선은 **CLIPScore**를 나타낸다. 여기서 우리는 **OAI CLIP-L/14**를 사전학습 모델로 사용한다. **$K \geq 5$가 되면 s-CLIPLoss가 모든 subtask metric에서 CLIPScore를 지속적으로 능가**하는 것을 볼 수 있다. 본 논문에서는 **$K=10$으로 설정**하였다. Table 7: **OpenAI의 CLIP-B/32 모델 또는 DFN의 공개 버전(DFN-P)만을 사용한 상위 방법들의 DataComp-medium 결과.** | OAI CLIP-B/32 | Dataset Size | IN-1k (1 sub-task) | IN Dist. Shift (5) | VTAB (11) | Retrieval (3) | Avg. (38) | | :--- | :--- | :--- | :--- | :--- | :--- | :--- | | CLIPScore (20%) | 22 M | 27.0 | 23.8 | 33.0 | 22.9 | 32.2 | | CLIPScore (30%) | 33 M | 27.6 | 24.2 | 33.6 | 25.1 | 33.2 | | s-CLIPLoss (20%) | 22 M | 28.9 | 24.8 | 34.3 | 24.3 | 33.0 | | s-CLIPLoss (30%) | 33 M | 28.8 | 25.1 | 33.7 | 26.6 | 33.6 | | s-CLIPLoss (30%) $\cap$ NormSim ${ }_{\infty}$ (Target) | 22 M | 32.4 | 27.4 | 35.9 | 26.3 | 35.2 | | DFN-P | | | | | | | | CLIPScore (15%) | 16M | 25.9 | 23.3 | 32.9 | 21.9 | 31.6 | | CLIPScore (17.5%) | 19M | 30.2 | 26.8 | 34.1 | 26.5 | 33.8 | | CLIPScore (20%) | 22 M | 29.7 | 26.8 | 33.0 | 27.0 | 33.1 | | CLIPScore (30%) | 33M | 28.4 | 24.7 | 33.2 | 26.8 | 32.7 | | s-CLIPLoss (15%) | 16M | 31.3 | 27.3 | $\underline{35.8}$ | 26.4 | 34.6 | | s-CLIPLoss (17.5%) | 19M | 31.2 | 27.5 | 35.7 | 27.0 | 34.7 | | s-CLIPLoss (20%) | 22 M | 30.7 | $\underline{27.4}$ | 33.6 | 27.5 | 33.8 | | s-CLIPLoss (30%) | 33M | 28.9 | 25.5 | 33.4 | 27.3 | 33.2 | | s-CLIPLoss (30%) $\cap$ NormSim $_{\infty}$ (Target) | 22 M | 29.4 | 23.6 | 33.5 | 24.2 | 32.5 | | s-CLIPLoss (17.5%) $\cap \operatorname{NormSim}_{\infty}($ Target $)$ | 16M | $\underline{31.5}$ | 26.4 | 34.6 | 25.4 | 34.4 | | s-CLIPLoss (17.5%) $\cap$ NormSim ${ }_{\infty}^{\mathrm{B} / 32}$ (Target) | 16M | 31.6 | 27.3 | 37.2 | 25.5 | 35.7 | ## D. 4 Vision-Only NormSim is Better than Using Both Vision and Language DataComp \[1]에서는 **이미지 기반 필터링이 텍스트 기반 필터링보다 우수함**을 보여준다. 본 논문에서도 이를 뒷받침하는 ablation study를 수행하였다. 계산 자원의 제약으로 인해, 우리는 **DataComp-small 데이터셋**에 대해 **$\mathrm{NormSim}_{2}$ (IN-1k)와 NormSim ${ }_{2}$-D**를 예시로 실행하였다. ImageNet-1k는 이미지를 설명하는 긴 텍스트 대신 레이블만 가지고 있기 때문에, **NormSim 2 (IN-1k)를 계산하기 전에 캡션을 생성**해야 한다. 우리는 오리지널 CLIP 논문 \[4]과 동일하게 **80개의 템플릿을 선택**하여 각 클래스에 대한 prompt를 생성하고, **해당 임베딩들의 평균을 해당 클래스 이미지의 대표 텍스트 임베딩으로 사용**하였다. 결과는 **Table 9**에 제시되어 있다. 두 가지 지표 모두에서 **"image only" > "image $\times$ text" > "text only"** 순서임을 확인할 수 있다. **NormSim$_{2}$ (IN-1k)**의 경우, **이미지 자체가 레이블로 생성된 텍스트 prompt보다 훨씬 더 많은 feature를 전달할 수 있기 때문**이라고 생각한다. **NormSim ${ }_{2}$-D**의 경우, **웹에서 수집된 데이터셋에 포함된 대량의 저품질 캡션과 관련**이 있을 것이다. 그리고 **"image $\times$ text"** 또한 **캡션의 정보성과 품질에 영향**을 받을 것이다. 요약하자면, **NormSim**에서는 **vision-only 임베딩을 사용하는 것이 가장 좋은 선택**이다. Table 8: NormSim ${ }_{\infty}$와 nearest neighbor selection 비교. OAI CLIP-L/14를 teacher model로 사용했으며, 두 방법 모두 s-CLIPLoss (30%)와 교차(intersected)되었다고 가정한다. 선택된 subset의 크기는 22M이다. | Filtering Strategy | IN-1k | VTAB | Avg. | | :--- | :---: | :---: | :---: | | s-CLIPLoss $(30 \%)$ | 27.9 | 33.2 | 32.9 | | Nearest Neibor Selection $^{4.5}$ | 31.5 | 34.9 | 34.0 | | NormSim $_{\infty}$ (Target) | $\mathbf{3 1 . 7}$ | $\mathbf{3 6 . 0}$ | $\mathbf{3 5 . 0}$ | Table 9: DataComp-small (11M)에서 NormSim 및 그 변형에 대한 Ablation Study. 모든 실험은 먼저 CLIP score를 기반으로 45%의 데이터를 선택한 다음, 해당 접근 방식을 사용하여 3.3M의 데이터를 얻는다. "image" 또는 "text"는 이미지 또는 텍스트 임베딩의 분산을 사용하여 $\bar{\Sigma}_{\text {target }}$를 나타내고, "image $\times$ text"는 이미지 및 텍스트 임베딩의 교차 공분산(cross-covariance)으로 $\bar{\Sigma}_{\text {target }}$를 나타낸다. | Filtering Strategy $\cap$ CLIP score (45%) | IN-1k | IN Dist. Shift | VTAB | Retrieval | Average | | :--- | :--- | :--- | :--- | :--- | :--- | | Random Sampling | 4.2 | 4.9 | 17.2 | 11.6 | 15.6 | | NormSim (IN-1k, image) | 5.2 | 5.5 | $\underline{19.0}$ | 12.2 | 17.4 | | NormSim (IN-1k, text) | 3.9 | 4.2 | 16.3 | 11.3 | 14.9 | | NormSim (IN-1k, image $\times$ text) | 4.3 | 4.9 | 17.5 | $\underline{11.8}$ | 15.9 | | NormSim-D (image) | $\underline{4.7}$ | 5.4 | 19.7 | 11.7 | $\underline{17.3}$ | | NormSim-D (text) | 3.5 | 4.1 | 16.7 | 11.1 | 15.4 | | NormSim-D (image $\times$ text) | 3.6 | 4.2 | 18.4 | 11.1 | 15.8 | ## E Additional Visualization 우리는 Figure 6, 7, 8에서 **다양한 s-CLIPLoss를 가진 더 많은 데이터**를 시각화하였다. Figure 9, 10, 11에서는 **NormSim $_{\infty}$ (Target)에 대해서도 유사하게 시각화**하였다.  Figure 6: DataComp-medium에서 **s-CLIPLoss 순위가 하위 100%인 작은 부분집합**의 시각화.  Figure 7: DataComp-medium에서 **s-CLIPLoss 순위가 하위 50%인 작은 부분집합**의 시각화.  Figure 8: DataComp-medium에서 **s-CLIPLoss 순위가 하위 10%인 작은 부분집합**의 시각화.  Figure 9: DataComp-medium에서 **NormSim $_{\infty}$ (Target) 순위가 상위 100%인 작은 부분집합**의 이미지 시각화.  Figure 10: DataComp-medium에서 **NormSim $_{\infty}$ (Target) 순위가 상위 50%인 작은 부분집합**의 이미지 시각화.  Figure 11: DataComp-medium에서 **NormSim $_{\infty}$ (Target) 순위가 상위 10%인 작은 부분집합**의 이미지 시각화. ## F NeurIPS Paper Checklist ## 1. Claims 질문: 초록과 서론에서 제시된 주요 주장들이 논문의 기여와 범위를 정확하게 반영하고 있는가? 답변: [Yes] 근거: 그렇다. 우리는 다음 사항들을 명확하게 정의한다: 1. 사용된 벤치마크; 2. 핵심 통찰력을 포함한 방법론; 3. 경험적 개선 사항. 가이드라인: - 답변 NA는 초록과 서론이 논문에서 제시된 주장을 포함하지 않음을 의미한다. - 초록 및/또는 서론은 논문의 기여, 중요한 가정 및 한계를 포함하여 제시된 주장을 명확하게 명시해야 한다. 이 질문에 대한 No 또는 NA 답변은 심사위원들에게 좋게 평가되지 않을 것이다. - 제시된 주장은 이론적 및 실험적 결과와 일치해야 하며, 결과가 다른 설정에 얼마나 일반화될 수 있는지 반영해야 한다. - 논문에서 달성되지 않은 목표라도 동기로서 포함하는 것은 괜찮지만, 이러한 목표가 논문에서 달성되지 않았다는 점이 명확해야 한다. ## 2. Limitations Question: Does the paper discuss the limitations of the work performed by the authors? Answer: [Yes] Justification: We discuss this briefly in the last section. Guidelines: - The answer NA means that the paper has no limitation while the answer No means that the paper has limitations, but those are not discussed in the paper. - The authors are encouraged to create a separate "Limitations" section in their paper. - The paper should point out any strong assumptions and how robust the results are to violations of these assumptions (e.g., independence assumptions, noiseless settings, model well-specification, asymptotic approximations only holding locally). The authors should reflect on how these assumptions might be violated in practice and what the implications would be. - The authors should reflect on the scope of the claims made, e.g., if the approach was only tested on a few datasets or with a few runs. In general, empirical results often depend on implicit assumptions, which should be articulated. - The authors should reflect on the factors that influence the performance of the approach. For example, a facial recognition algorithm may perform poorly when image resolution is low or images are taken in low lighting. Or a speech-to-text system might not be used reliably to provide closed captions for online lectures because it fails to handle technical jargon. - The authors should discuss the computational efficiency of the proposed algorithms and how they scale with dataset size. - If applicable, the authors should discuss possible limitations of their approach to address problems of privacy and fairness. - While the authors might fear that complete honesty about limitations might be used by reviewers as grounds for rejection, a worse outcome might be that reviewers discover limitations that aren't acknowledged in the paper. The authors should use their best judgment and recognize that individual actions in favor of transparency play an important role in developing norms that preserve the integrity of the community. Reviewers will be specifically instructed to not penalize honesty concerning limitations. --- [Korean Translation] Question: Does the paper discuss the limitations of the work performed by the authors? Answer: [Yes] Justification: 우리는 마지막 섹션에서 이에 대해 간략하게 논의한다. Guidelines: - 답변 'NA'는 논문에 한계점이 없음을 의미하며, 'No'는 논문에 한계점이 있지만 논문에서 논의되지 않았음을 의미한다. - 저자들은 논문에 별도의 "Limitations" 섹션을 만들 것을 권장한다. - 논문은 어떠한 **강력한 가정**이 있었는지, 그리고 이러한 가정이 위반될 경우 결과가 얼마나 **강건한지**를 지적해야 한다 (예: 독립성 가정, 노이즈 없는 설정, 모델의 적절한 명세, 국소적으로만 유효한 점근적 근사 등). 저자들은 이러한 가정이 실제 상황에서 어떻게 위반될 수 있으며, 그 함의가 무엇인지 숙고해야 한다. - 저자들은 **주장의 범위**에 대해 숙고해야 한다. 예를 들어, 접근 방식이 소수의 데이터셋이나 소수의 실행으로만 테스트되었는지 여부 등. 일반적으로, **경험적 결과는 종종 암묵적인 가정에 의존**하므로, 이를 명확히 밝혀야 한다. - 저자들은 **접근 방식의 성능에 영향을 미치는 요인**에 대해 숙고해야 한다. 예를 들어, 얼굴 인식 알고리즘은 이미지 해상도가 낮거나 저조도 환경에서 촬영된 이미지에서 성능이 저하될 수 있다. 또는 음성-텍스트 변환 시스템은 기술 전문 용어를 처리하지 못하여 온라인 강의의 자막을 안정적으로 제공하는 데 사용될 수 없을 수 있다. - 저자들은 제안된 알고리즘의 **계산 효율성**과 **데이터셋 크기에 따른 확장성**에 대해 논의해야 한다. - 해당되는 경우, 저자들은 **프라이버시 및 공정성 문제**를 해결하기 위한 접근 방식의 **가능한 한계점**에 대해 논의해야 한다. - 저자들은 한계점에 대한 완전한 솔직함이 심사위원들에게 거절의 근거로 사용될까 두려워할 수 있지만, 더 나쁜 결과는 심사위원들이 논문에서 인정되지 않은 한계점을 발견하는 것일 수 있다. 저자들은 최선의 판단을 사용하고, 투명성을 위한 개별적인 행동이 커뮤니티의 무결성을 보존하는 규범을 개발하는 데 중요한 역할을 한다는 것을 인식해야 한다. 심사위원들은 한계점에 대한 솔직함에 대해 불이익을 주지 않도록 특별히 지시받을 것이다. ## 3. Theory Assumptions and Proofs **질문**: 각 이론적 결과에 대해, 논문은 모든 가정과 완전하고 (정확한) 증명을 제공하는가? **정당화**: NormSim 결과에 대한 이론의 전체 버전은 Appendix A에 있으며, 우리는 모든 가정과 증명을 제공한다. 우리는 Sec. 3.2에서 이를 간략하게 언급했다. **가이드라인**: * 답변 NA는 논문에 이론적 결과가 포함되어 있지 않음을 의미한다. * 논문의 모든 정리, 공식, 증명은 번호가 매겨지고 상호 참조되어야 한다. * 모든 가정은 정리의 진술에서 명확하게 명시되거나 참조되어야 한다. * 증명은 본 논문이나 보충 자료에 나타날 수 있지만, 보충 자료에 나타나는 경우 저자는 직관을 제공하기 위해 짧은 증명 스케치를 제공하는 것이 좋다. * 반대로, 논문의 핵심에 제공된 비공식적인 증명은 부록이나 보충 자료에 제공된 공식적인 증명으로 보완되어야 한다. * 증명이 의존하는 정리와 보조정리는 적절하게 참조되어야 한다. ## 4. Experimental Result Reproducibility Question: Does the paper fully disclose all the information needed to reproduce the main experimental results of the paper to the extent that it affects the main claims and/or conclusions of the paper (regardless of whether the code and data are provided or not)? Answer: [Yes] Justification: 주요 결과는 Section 4에 제시되어 있다. 또한, Appendix C에 실험 세부사항이 제공되어 있다. ## Guidelines: * **NA** 답변은 해당 논문에 실험이 포함되어 있지 않음을 의미한다. * 논문에 실험이 포함되어 있다면, 이 질문에 대한 **No** 답변은 심사위원들에게 좋게 받아들여지지 않을 것이다. 코드와 데이터 제공 여부와 관계없이, 논문을 재현 가능하게 만드는 것은 중요하다. * 기여가 데이터셋 및/또는 모델인 경우, 저자는 결과의 재현성 또는 검증 가능성을 위해 취한 단계를 설명해야 한다. * 기여에 따라 재현성은 다양한 방식으로 달성될 수 있다. 예를 들어, 기여가 새로운 아키텍처인 경우, 아키텍처를 완전히 설명하는 것으로 충분할 수 있으며, 특정 모델 및 실증적 평가가 기여인 경우, 다른 사람들이 동일한 데이터셋으로 모델을 복제할 수 있도록 하거나 모델에 대한 접근을 제공해야 할 수도 있다. 일반적으로 코드와 데이터를 공개하는 것이 이를 달성하는 좋은 방법이지만, 재현성은 결과를 복제하는 방법에 대한 자세한 지침, 호스팅된 모델에 대한 접근(예: 대규모 언어 모델의 경우), 모델 체크포인트 공개 또는 수행된 연구에 적합한 다른 수단을 통해서도 제공될 수 있다. * NeurIPS는 코드 공개를 요구하지 않지만, 모든 제출물은 재현성을 위한 합리적인 방법을 제공해야 하며, 이는 기여의 성격에 따라 달라질 수 있다. 예를 들어: (a) 기여가 주로 새로운 알고리즘인 경우, 논문은 해당 알고리즘을 재현하는 방법을 명확히 해야 한다. (b) 기여가 주로 새로운 모델 아키텍처인 경우, 논문은 아키텍처를 명확하고 완전하게 설명해야 한다. (c) 기여가 새로운 모델(예: 대규모 언어 모델)인 경우, 결과를 재현하기 위해 이 모델에 접근할 수 있는 방법이 있거나 모델을 재현할 수 있는 방법(예: 오픈 소스 데이터셋 또는 데이터셋을 구성하는 방법에 대한 지침)이 있어야 한다. (d) 우리는 일부 경우에 재현성이 까다로울 수 있음을 인지하며, 이 경우 저자는 재현성을 위해 제공하는 특정 방법을 설명할 수 있다. 비공개 소스 모델의 경우, 모델에 대한 접근이 어떤 식으로든 제한될 수 있지만(예: 등록된 사용자에게만), 다른 연구자들이 결과를 재현하거나 검증할 수 있는 경로가 있어야 한다. ## 5. Open access to data and code Question: Does the paper provide open access to the data and code, with sufficient instructions to faithfully reproduce the main experimental results, as described in supplemental material? Answer: [Yes] Justification: 코드는 NeurIPS 코드 제출 가이드라인에 따라 제공될 예정이다. 논문이 채택된 후 오픈 소스로 공개할 것이다. Guidelines: - 답변 NA는 논문에 코드를 필요로 하는 실험이 없음을 의미한다. - 자세한 내용은 NeurIPS 코드 및 데이터 제출 가이드라인(https://nips.cc/public/guides/CodeSubmissionPolicy)을 참조하라. - 코드와 데이터 공개를 권장하지만, 이것이 불가능할 수도 있음을 이해하므로 "No"도 허용되는 답변이다. (예: 새로운 오픈 소스 벤치마크와 같이 기여의 핵심인 경우가 아니라면) 코드를 포함하지 않았다는 이유만으로 논문이 거절될 수는 없다. - 지침에는 결과를 재현하는 데 필요한 정확한 명령과 환경이 포함되어야 한다. 자세한 내용은 NeurIPS 코드 및 데이터 제출 가이드라인(https://nips.cc/public/guides/CodeSubmissionPolicy)을 참조하라. - 저자는 원본 데이터, 전처리된 데이터, 중간 데이터, 생성된 데이터 등에 접근하고 준비하는 방법을 포함하여 데이터 접근 및 준비에 대한 지침을 제공해야 한다. - 저자는 새로 제안된 방법과 baseline에 대한 모든 실험 결과를 재현하는 스크립트를 제공해야 한다. 만약 실험의 일부만 재현 가능하다면, 어떤 부분이 스크립트에서 생략되었고 그 이유는 무엇인지 명시해야 한다. - 제출 시점에는 익명성을 유지하기 위해 저자는 익명화된 버전(해당하는 경우)을 공개해야 한다. - 보충 자료(논문에 첨부)에 가능한 한 많은 정보를 제공하는 것이 권장되지만, 데이터 및 코드에 대한 URL을 포함하는 것도 허용된다. ## 6. Experimental Setting/Details Question: Does the paper specify all the training and test details (e.g., data splits, hyperparameters, how they were chosen, type of optimizer, etc.) necessary to understand the results? Answer: [Yes] Justification: 주요 결과는 Sec4에 제시되어 있다. 또한, Appendix C에 실험 세부사항이 제공된다. Guidelines: - The answer NA means that the paper does not include experiments. - The experimental setting should be presented in the core of the paper to a level of detail that is necessary to appreciate the results and make sense of them. - The full details can be provided either with the code, in appendix, or as supplemental material. ## 7. Experiment Statistical Significance Question: Does the paper report error bars suitably and correctly defined or other appropriate information about the statistical significance of the experiments? Answer: [No] Justification: DFN, HYPE, MLM과 같은 거의 모든 기존 연구들은 DataComp-medium에서 학습을 한 번만 실행한다. 128M 크기의 데이터셋으로 학습하는 것은 매우 비용이 많이 들고 상대적으로 안정적이기 때문에, 일반적으로 다른 학습 seed로 실험을 다시 실행할 필요가 없다고 여겨진다. 실험에서는 공정한 비교를 위해 모든 학습 seed를 0으로 고정한다. 우리 알고리즘의 대부분은 결정론적이다. 무작위성을 포함하는 유일한 부분은 $\mathrm{K}=10$번의 재샘플링이 필요한 s-CLIPLoss이다. 이에 대해서는 Fig. 5에서 민감도 분석을 제공한다. Guidelines: - 답변 NA는 논문에 실험이 포함되어 있지 않음을 의미한다. - 논문의 주요 주장을 뒷받침하는 실험에 대해 최소한 **오차 막대(error bars), 신뢰 구간(confidence intervals), 또는 통계적 유의성 검정**이 결과와 함께 제시된 경우 저자는 "Yes"라고 답변해야 한다. - 오차 막대가 포착하는 **변동 요인**이 명확하게 명시되어야 한다 (예: train/test 분할, 초기화, 특정 파라미터의 무작위 추출, 또는 주어진 실험 조건에서의 전체 실행). - 오차 막대 계산 방법이 설명되어야 한다 (닫힌 형식 공식, 라이브러리 함수 호출, 부트스트랩 등). - 가정된 내용이 제시되어야 한다 (예: 정규 분포 오차). - 오차 막대가 **표준 편차(standard deviation)인지 평균의 표준 오차(standard error of the mean)인지** 명확해야 한다. - 1-sigma 오차 막대를 보고하는 것은 허용되지만, 이를 명시해야 한다. 오차의 정규성 가설이 검증되지 않은 경우, 저자는 96% CI를 명시하는 것보다 2-sigma 오차 막대를 보고하는 것이 바람직하다. - 표나 그림에 오차 막대가 보고된 경우, 저자는 텍스트에서 **오차 막대가 어떻게 계산되었는지 설명하고 해당 그림이나 표를 참조**해야 한다. - 비대칭 분포의 경우, 저자는 결과가 범위를 벗어나는 (예: 음수 오류율) 대칭 오차 막대를 표나 그림에 표시하지 않도록 주의해야 한다. ## 8. Experiments Compute Resources Question: For each experiment, does the paper provide sufficient information on the computer resources (type of compute workers, memory, time of execution) needed to reproduce the experiments? Answer: [Yes] Justification: 우리는 **Appendix C.1**에서 **컴퓨팅 비용 추정 및 비교**에 대해 논의한다. **DataComp 벤치마크**에서는 메모리 사용량이 상당히 표준적이기 때문에 명시적으로 계산하지 않았다. Guidelines: - 답변 NA는 논문에 실험이 포함되어 있지 않음을 의미한다. - 논문은 CPU 또는 GPU, 내부 클러스터 또는 클라우드 제공업체 등 **컴퓨팅 작업자의 유형**을 명시해야 하며, 관련 **메모리 및 저장 공간**을 포함해야 한다. - 논문은 **각 개별 실험 실행에 필요한 컴퓨팅 양**을 제공하고 **총 컴퓨팅 양을 추정**해야 한다. - 논문은 **전체 연구 프로젝트에 논문에 보고된 실험보다 더 많은 컴퓨팅이 필요했는지 여부** (예: 논문에 포함되지 않은 예비 또는 실패한 실험)를 공개해야 한다. ## 9. Code Of Ethics Question: Does the research conducted in the paper conform, in every respect, with the NeurIPS Code of Ethics https://neurips.cc/public/EthicsGuidelines? Answer: [Yes] Justification: Yes Guidelines: - The answer NA means that the authors have not reviewed the NeurIPS Code of Ethics. - If the authors answer No, they should explain the special circumstances that require a deviation from the Code of Ethics. - The authors should make sure to preserve anonymity (e.g., if there is a special consideration due to laws or regulations in their jurisdiction). 10. Broader Impacts Question: Does the paper discuss both potential positive societal impacts and negative societal impacts of the work performed? Answer: [NA] Justification: This research focuses on the methodology part of data selection. All experiments are performed under the existing standard dataset. So as long as those datasets itself maybe harmless, our research will not make any negative impact. Guidelines: - The answer NA means that there is no societal impact of the work performed. - If the authors answer NA or No, they should explain why their work has no societal impact or why the paper does not address societal impact. - Examples of negative societal impacts include potential malicious or unintended uses (e.g., disinformation, generating fake profiles, surveillance), fairness considerations (e.g., deployment of technologies that could make decisions that unfairly impact specific groups), privacy considerations, and security considerations. - The conference expects that many papers will be foundational research and not tied to particular applications, let alone deployments. However, if there is a direct path to any negative applications, the authors should point it out. For example, it is legitimate to point out that an improvement in the quality of generative models could be used to generate deepfakes for disinformation. On the other hand, it is not needed to point out that a generic algorithm for optimizing neural networks could enable people to train models that generate Deepfakes faster. - The authors should consider possible harms that could arise when the technology is being used as intended and functioning correctly, harms that could arise when the technology is being used as intended but gives incorrect results, and harms following from (intentional or unintentional) misuse of the technology. - If there are negative societal impacts, the authors could also discuss possible mitigation strategies (e.g., gated release of models, providing defenses in addition to attacks, mechanisms for monitoring misuse, mechanisms to monitor how a system learns from feedback over time, improving the efficiency and accessibility of ML). ## 11. Safeguards Question: Does the paper describe safeguards that have been put in place for responsible release of data or models that have a high risk for misuse (e.g., pretrained language models, image generators, or scraped datasets)? Answer: [NA] Justification: 이 논문은 기존 데이터셋(DataComp-medium \[1])에서 선택된 데이터의 UID만 제공할 것이다. 이 논문은 어떠한 모델이나 새로운 데이터셋도 공개하지 않을 것이다. Guidelines: - NA는 논문이 그러한 위험을 제기하지 않음을 의미한다. - 오용 위험이 높은 모델(예: 사전학습된 언어 모델, 이미지 생성기 또는 스크랩된 데이터셋)은 모델의 통제된 사용을 허용하기 위한 필요한 안전 장치와 함께 공개되어야 한다. 예를 들어, 사용자가 사용 지침을 준수하도록 요구하거나 모델 접근을 제한하거나 안전 필터를 구현하는 방식 등이 있다. - 인터넷에서 스크랩된 데이터셋은 안전 위험을 초래할 수 있다. 저자는 안전하지 않은 이미지 공개를 피하기 위해 어떻게 노력했는지 설명해야 한다. - 효과적인 안전 장치를 제공하는 것이 어렵고, 많은 논문에서 이를 요구하지 않는다는 점을 인지하지만, 저자들이 이를 고려하고 최선을 다해 노력할 것을 권장한다. ## 12. Licenses for existing assets Question: Are the creators or original owners of assets (e.g., code, data, models), used in the paper, properly credited and are the license and terms of use explicitly mentioned and properly respected? Answer: [Yes] Justification: 우리는 데이터셋 URL과 벤치마크 구현에 사용된 코드/모델을 소개하는 DataComp \[1]을 인용한다. Guidelines: * NA라는 답변은 논문에서 기존 자산을 사용하지 않았음을 의미한다. * 저자는 코드 패키지 또는 데이터셋을 생성한 원본 논문을 인용해야 한다. * 저자는 사용된 자산의 버전을 명시하고, 가능하다면 URL을 포함해야 한다. * 각 자산에 대해 라이선스 이름(예: CC-BY 4.0)이 포함되어야 한다. * 특정 출처(예: 웹사이트)에서 스크랩된 데이터의 경우, 해당 출처의 저작권 및 서비스 약관이 제공되어야 한다. * 자산이 공개되는 경우, 패키지에 라이선스, 저작권 정보 및 사용 약관이 제공되어야 한다. 인기 있는 데이터셋의 경우, paperswithcode.com/datasets에서 일부 데이터셋에 대한 라이선스를 큐레이션하고 있다. 해당 라이선스 가이드는 데이터셋의 라이선스를 결정하는 데 도움이 될 수 있다. * 재패키징된 기존 데이터셋의 경우, 원본 라이선스와 파생 자산의 라이선스(변경되었다면)가 모두 제공되어야 한다. * 이 정보가 온라인에서 제공되지 않는 경우, 저자는 자산의 생성자에게 연락하는 것이 권장된다. ## 13. New Assets **질문**: 논문에서 소개된 새로운 asset들이 잘 문서화되어 있으며, 해당 문서가 asset과 함께 제공되는가? **답변**: [NA] **근거**: 본 논문은 새로운 asset을 공개하지 않는다. **가이드라인**: * 답변 NA는 논문이 새로운 asset을 공개하지 않음을 의미한다. * 연구자들은 제출 시 구조화된 템플릿을 통해 데이터셋/코드/모델에 대한 세부 정보(학습 방식, 라이선스, 한계점 등)를 전달해야 한다. * 논문은 asset이 사용된 사람들의 동의를 얻었는지 여부와 그 방법에 대해 논의해야 한다. * 제출 시 asset을 익명화해야 한다 (해당하는 경우). 익명화된 URL을 생성하거나 익명화된 zip 파일을 포함할 수 있다. ## 14. Crowdsourcing and Research with Human Subjects Question: 크라우드소싱 실험 및 인간 대상 연구와 관련하여, 본 논문은 참가자에게 제공된 지침의 전체 텍스트와 해당되는 경우 스크린샷, 그리고 보상(있는 경우)에 대한 세부 정보를 포함하고 있는가? Answer: [NA] Justification: 본 논문은 크라우드소싱이나 인간 대상 연구를 포함하지 않는다. 모든 지표는 고정된 평가이다. Guidelines: - 답변 NA는 본 논문이 크라우드소싱이나 인간 대상 연구를 포함하지 않음을 의미한다. - 이 정보가 보충 자료에 포함되어 있어도 괜찮지만, 논문의 주요 기여가 인간 대상 연구와 관련된 경우 가능한 한 많은 세부 정보가 본 논문에 포함되어야 한다. - NeurIPS 윤리 강령에 따르면, 데이터 수집, 큐레이션 또는 기타 노동에 참여하는 작업자는 데이터 수집 국가의 최저 임금 이상을 받아야 한다. ## 15. Institutional Review Board (IRB) Approvals or Equivalent for Research with Human Subjects **질문**: 본 논문이 연구 참여자에게 발생할 수 있는 잠재적 위험, 그러한 위험이 피험자에게 공개되었는지 여부, 그리고 기관윤리심의위원회(IRB) 승인(또는 해당 국가나 기관의 요구사항에 따른 동등한 승인/심의)을 받았는지 여부를 기술하고 있는가? **답변**: [해당 없음] **근거**: 본 논문은 크라우드소싱이나 인간 피험자를 대상으로 한 연구를 포함하지 않는다. ## Guidelines: * **NA**라는 답변은 해당 논문이 **크라우드소싱(crowdsourcing)이나 인간 피험자를 대상으로 한 연구를 포함하지 않음**을 의미한다. * 연구가 수행되는 국가에 따라, **인간 피험자 연구에 대해서는 IRB 승인(또는 이에 상응하는 승인)이 요구될 수 있다.** IRB 승인을 받았다면, 논문에 이를 명확히 명시해야 한다. * 우리는 이러한 절차가 기관 및 지역에 따라 크게 다를 수 있음을 인지하며, 저자들은 **NeurIPS 윤리 강령(Code of Ethics)과 소속 기관의 지침을 준수**할 것을 기대한다. * 초기 제출 시에는 **익명성을 해칠 수 있는 어떠한 정보도 포함하지 않아야 한다** (해당하는 경우), 예를 들어 검토를 수행하는 기관명 등.